Моделирование задач (Полет тела, брошенного под углом к горизонту).
Здесь возможны модификации:
Попадание в заданную площадку.
Попадание в стенку с указанной высотой.
Задание 1: Формальная модель «Попадание в площадку тела, брошенного под углом к горизонту». Построить формальную модель решения задачи «Попадание в площадку тела, брошенного под углом к горизонту». В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в площадку определенной длины, находящуюся на известном расстоянии.
Содержательная постановка задачи. В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в площадку определенного размера, находящуюся на известном расстоянии.
Качественная описательная модель. Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятий и законов, т.е. в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:
мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;
изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g=9,8 м/с2 и движение по оси Y можно считать равноускоренным;
скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси X можно считать равномерным.
Формальная модель. Движение мячика по оси Х равномерное, а по оси Y равноускоренное, поэтому для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости v0 и угле бросания α значения координат дальности полета x и высоты y от времени можно описать следующими формулами:
x = v0·cosα·t
y = v0·sinα·t – g·t2/2
Площадка расположена на поверхности земли, поэтому из второй формулы можно выразить время, которое понадобится мячику, чтобы достичь площадки:
v0·sinα·t – g·t2/2 = 0
t·(v0·sinα – g·t/2) = 0
Значение времени t = 0 не имеет физического смысла, поэтому:
v0·sinα – g·t/2 = 0
t = (2·v0·sinα)/g
Подставим полученное выражение для времени в формулу для вычисления координаты х:
x = (v0·cosα·2·v0·sinα)/g = (v02·sin2α)/g
Формализуем теперь условие попадание мячика в площадку. Пусть площадка расположена на расстоянии s и имеет длину L. Тогда попадание произойдет, если значение координаты х мячика будет удовлетворять условию в форме неравенства:
s ≤ х ≤ s+L
Если хs, то это означает "недолет", а если хs+L, то это означает "перелет".
Заготовка программы для попадания в площадку:
program ploschadka;
uses graphABC, crt;
const xc=40; yc=240; s=300;
m=20; n=7; step=0.01; g=9.8;
var
x,y,t,a,v0,da:real;
xe,ye:integer; i:integer;
begin clrscr;
{возможен ввод начального угла в градусах:
write('a =');readln(a); a:=a*pi/180;}
write('v0='); readln(v0);
line(xc,10,xc,470);
line(10,yc,630,yc);
a:=pi/20; da:=pi/(6*n);
for i:=1 to n do
begin
a:=a+da;
t:=0;
repeat
x:=v0*cos(a)*t;
y:=v0*sin(a)*t-g*t*t/2;
xe:=round(xc+m*x);
ye:=round(yc-m*y);
setpixel(xe,ye,2);
t:=t+step;
until (ts/(v0*cos(a))) or (yeyc);
end;
end.
Задание:
Реализовать программу на компьютере. Оценить результат. C какой скоростью V0 и начальном угле a при заданном значении n будет зафиксировано наибольшее число попаданий в площадку? Результат записать в тетрадь для проверочных работ.
Разработать формальную модель при условии попадания мячика в стенку высотой h. Записать выкладки с пояснениями в тетрадь для проверочных работ.
Модифицировать программу таким образом, чтобы при попадании в стенку траектория полета мячика за стенкой не имела продолжения. Программу записать в тетрадь для проверочных работ.
Найти диапазон скоростей и углов для попадания в стенку.
C какой скоростью при заданном значении n будет зафиксировано наибольшее число попаданий в стенку? Результат записать в тетрадь для проверочных работ.
Приложение к программе:
Построение делений по оси y:
xt:=10; dx:=10
For i:=1 to 62 do
Begin
xt:=xt+dx;
line(xt,yc,xt,yc-5);
end;
Построение стенки высотой h на расстоянии s0:
line(s0,yc,s0,yc-h);
Соотношение для угла видимости ah (в радианах) верхней границы стенки высотой h на расстоянии s0:
ah:=arctan(2*h/s0); da:=ah/n;
Задание 2: Компьютерная модель «Попадание в площадку тела, брошенного под углом к горизонту»в электронных таблицах. На основе формальной модели «Попадание в площадку тела, брошенного под углом к горизонту» построить и исследовать компьютерную модель в электронных таблицах StarOffice Calc ( В ДАННОЙ РАБОТЕ СООТВЕТСТВУЮТ ВСЕ КОМАНДЫ В Microsoft Excel). Поэтому работаем в Microsoft Excel.
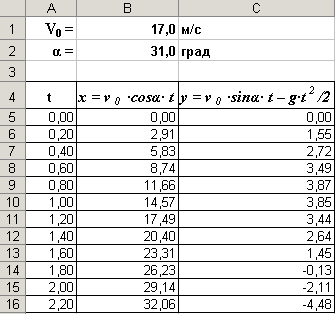
Выделим в таблице определенные ячейки для ввода значений начальной скорости v0 и угла α и вычислим по формулам 3.1 значения координат тела x и y для определенных значений времени t с заданным интервалом.
Для преобразования значений углов из градусов в радианы используем функцию РАДИАНЫ().
|
| Проект «Движение тела, брошенного под углом к горизонту» |
| 1 | Запустить электронные таблицы Microsoft Excel. Для ввода начальной скорости будем использовать ячейку B1, а для ввода угла – ячейку B2. |
|
| 2 | Введем в ячейки A5:A16 значения времени с интервалом в 0,2 с. | |
| 3 | В ячейки B5 и C5 введем формулы: =$B$1*COS(РАДИАНЫ($B$2))*A5 =$B$1*SIN(РАДИАНЫ($B$2))*A5-4,9*A5*A5 | |
| 4 | Скопируем формулы в ячейки В6:В16 и С6:С16 соответственно. |
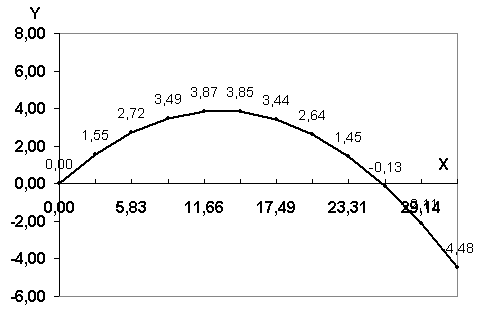
Визуализируем модель, построив график зависимости координаты y от координаты x (траекторию движения тела).
| 5 | Построить диаграмму типа График, в которой используется в качестве категории диапазон ячеек B5:B16, а в качестве значений - диапазон ячеек С5:С16. |
|
Исследуем модель и определим с заданной точностью 0,1 градуса значения диапазона изменений угла, которые обеспечивают попадание в площадку, находящуюся на расстоянии 25 м и длиной 2 м, при заданной начальной скорости 17 м/с. Воспользуемся для этого методом Подбор параметра.
| 6 | Установить для ячеек точность один знак после запятой. | |||
| 7 | Ввести в ячейки B19 и B20 значения начальной скорости V0 = 17 м/c и угла α = 31 град, а в ячейку B22 формулу для вычисления координаты X мячика для заданных начальных условий: =B19^2*SIN(РАДИАНЫ(2*B20))/9,81 |
|
| |
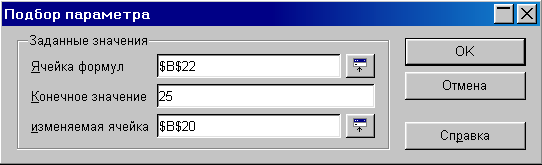
| 8 | Выделить ячейку В22 и ввести команду [Сервис-Подбор параметра…]. На появившейся диалоговой панели ввести в поле Конечное значение координату ближнего края площадки – 25. В поле изменяемая ячейка ввести адрес ячейки, содержащей значение угла (в данном случае $В$20). |
| ||
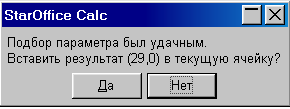
| 9 | После щелчка по кнопке Да на появившейся панели StarOffice Calc в ячейку В20 будет записано значение 29,0. |
| ||
| 10 | Повторить процедуру подбора параметра для попадания в дальний край площадки, в ячейке В20 получим значение 33,2. Таким образом, существует диапазон значений угла бросания от 29,0 до 33,2 градусов, в котором обеспечивается попадание в площадку. | |||
| 11 | Повторить процедуру определения диапазона углов при начальном значении 55 град, получим значения предельных углов 56,8 и 61,0 градуса. С учетом точности вычислений данные для обоих диапазонов углов подтверждают результаты, полученные при исследовании компьютерной модели на языке ABCPascal | |||
program stenka1;
uses graphABC,Crt;
const xc=40; {нач. коорд. по Х}
yc=240;{нач. коорд. по У}
h=50; {высота стенки}
s=300; {расстояние до стенки}
m=10; {множитель, через сколько пикселей ставится точка}
n=7; {число бросков}
step=0.005; {шаг по времени}
g=9.8; {ускорение св. падения}
var
x,y,t,a,v0,ah,da:real;
xe,ye:integer; i:integer;
begin
clrscr;
{write('угол в градусах a =');readln(a); a:=a*pi/180;}
write('нач. скорость в м/с v0='); readln(v0);
line(xc,10,xc,470);
line(10,yc,630,yc);
line(s,yc,s,yc-h);
ah:=arctan(3*h/s); {максимальный угол броска}
da:=ah/n; {промежуток в радианах между бросками}
a:=0; {нач. угол}
for i:=1 to n do
begin
a:=a+da;
t:=0;
repeat
x:=v0*cos(a)*t;
y:=v0*sin(a)*t-g*t*t/2;
xe:=round(xc+m*x);
ye:=round(yc-m*y);
setpixel(xe,ye,2);
t:=t+step;
until (ts/(v0*cos(a))) or (yeyc);
end;
end.
program stenka2;
uses graphABC,Crt;
const
xc=40; {нач. коорд. по Х}
yc=240;{нач. коорд. по У}
h=50; {высота стенки}
s=300; {расстояние до стенки}
m=10; {множитель, через сколько пикселей ставится точка}
n=7; {число бросков}
step=0.005; {шаг по времени}
g=9.8; {ускорение св. падения}
var
x,y,t,a,v0,ah,da:real;
xe,ye:integer; i:integer;
begin
clrscr;
{write('угол в градусах a =');readln(a); a:=a*pi/180;}
write('нач. скорость в м/с v0='); readln(v0);
line(xc,10,xc,470);
line(10,yc,630,yc);
line(s,yc,s,yc-h);
ah:=arctan(3*h/s); {максимальный угол броска}
da:=ah/n; {промежуток в радианах между бросками}
a:=0; {нач. угол}
for i:=1 to n do
begin
a:=a+da;
t:=0;
repeat
x:=v0*cos(a)*t;
y:=v0*sin(a)*t-g*t*t/2;
xe:=round(xc+m*x);
ye:=round(yc-m*y);
if (ye(yc-h)) and not(xes) then
setpixel(xe,ye,2);
if (ye
setpixel(xe,ye,2);
t:=t+step;
until (ts/(v0*cos(a))) or (yeyc);
end;
end.
3

 Получите свидетельство
Получите свидетельство Вход
Вход













 Моделирование по теме "Тело брошенное под углом к горизонту" (96.5 KB)
Моделирование по теме "Тело брошенное под углом к горизонту" (96.5 KB)
 0
0 5514
5514 208
208 Нравится
0
Нравится
0


