Методика работы над признаком параллельности прямой и плоскости

Методика работы над теоремой: «Признак параллельности прямой и плоскости»

1. Мотивация.

-Сформулируйте определение, когда прямая и плоскость являются параллельными?

-прямая и плоскость называются параллельными, если они не имеют общих точек.

-Как вы считаете, будет ли линия пересечения потолка и стены параллельна плоскости пола? (не знают, но предположат, что да)

-Будет ли ребро куба параллельно противоположной грани?

-возможно.

-Можете ли вы быть уверены в том, что, например, троллейбусные провода никогда не будут иметь общих точек с плоскостью земли? Что ребро куба никогда не пересечется с противоположной гранью? И т.д.

-нет.

-Значит, нам нужно каким-то образом выяснить это, узнать новую теорему или признак, по которому мы сможем точно ответить на данные вопросы. А еще это нам понадобится при решении задач, где надо установить параллельность прямой и плоскости.

2. Раскрытие содержания теоремы.

На стол положить карандаш.

-Что вы можете сказать о взаимном расположении карандаша и поверхности стола?

-карандаш лежит в плоскости стола.

Ручку расположить так, чтобы она была параллельна карандашу. (но не на столе)

-Что можно сказать о взаимном расположении карандаша и ручки?

-Они параллельны, так как не имеют общих точек.

Что вы можете сказать о взаимном расположении ручки и поверхности стола?

-Они также параллельны, т.е. ручка не лежит в плоскости стола.

-Сделайте вывод, основываясь на опыте.

-если какая-то прямая, не лежащая в плоскости параллельна прямой, лежащей в некоторой плоскости, то она параллельна этой плоскости.

Или вернуться к мотивационным задачам и поставить следующий вопрос:

• Что в поставленных задачах известно о данных прямых и каков предполагаемый ответ?

3. Мотивация необходимости доказательства теоремы.

- Ребята, мы с вами определили, что, если какая-то прямая, не лежащая в плоскости параллельна прямой, лежащей в плоскости, то она параллельна этой плоскости только на основе предположения, которое мы выдвинули, разбирая пример со столом, ручкой и карандашом. А вдруг мы не рассмотрели случай, когда параллельности плоскости и прямой не будет наблюдаться? Чтобы убрать все сомнения докажем нашу гипотезу.

4. Формулировка теоремы, работа над ее структурой.

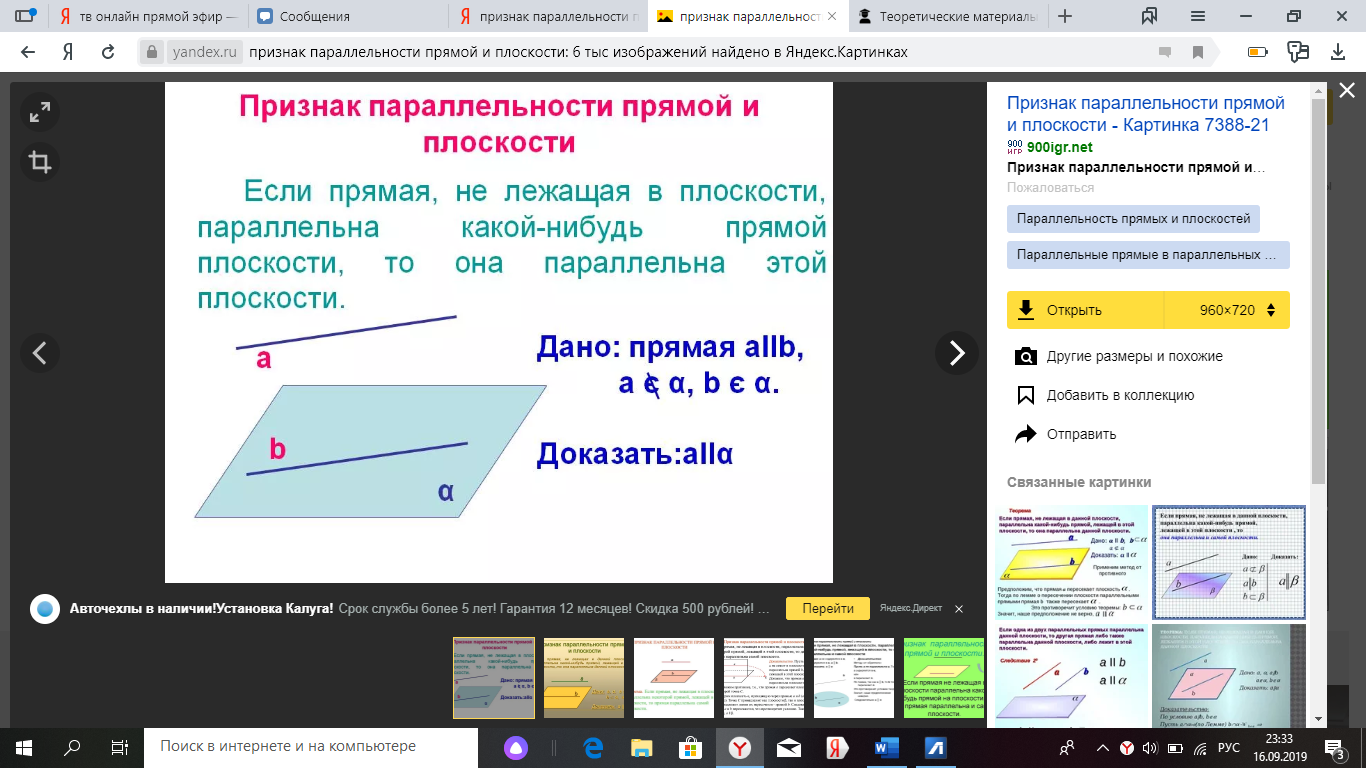
Гипотеза, которую вы выдвинули является признаком параллельности прямой и плоскости. Сформулируем его: если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

- Выделите условие и заключение теоремы.

- условие: дана прямая, не лежащая в данной плоскости.

- заключение: эта прямая параллельна данной плоскости.

5. Поиск доказательства теоремы.

-Как вы считаете, с чего нужно начать доказательство? (с чертежа, записи того, что дано и что нужно доказать)

- Что дано в теореме? (прямая, не лежащая в данной плоскости, которая параллельна какой-нибудь другой прямой, лежащей в этой плоскости.)

- Что нужно доказать? (что если прямая, не лежащая в плоскости параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости)

- Для того, чтобы доказать данный признак, как вы думаете, с чего нам начать, если даны 2 параллельные прямые? (нужно доказать, что одна из прямых, например, прямая, не лежащая в данной плоскости (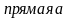 ), параллельна плоскости)

-Откуда может следовать вывод о параллельности прямой и плоскости, каким известным утверждением можно для этого воспользоваться? (определение параллельности прямой и плоскости: прямая и плоскость называются параллельными, если они не имеют общих точек)

-Но можно ли в данном случае воспользоваться определением? (нет, так как признак, указанный в определении, не поддается проверке)

- Вспомните из планиметрии, какой способ мы применяли для доказательства при невозможности проверить выполнение какого - либо признака? (метод «от противного»)

- Воспользуемся данным методом и предположим, что прямая пересекает плоскость. Какое противоречие получим? (по Лемме о пересечении плоскости параллельными прямыми: если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость: т.е. другая прямая 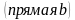также должна пересекать плоскость, а это невозможно, так как другая прямая лежит в данной плоскости)

- Какой вывод сделаем? (прямая a не пересекает плоскость, а, следовательно, параллельна плоскости)

- Верно. Переходим к оформлению доказательства.

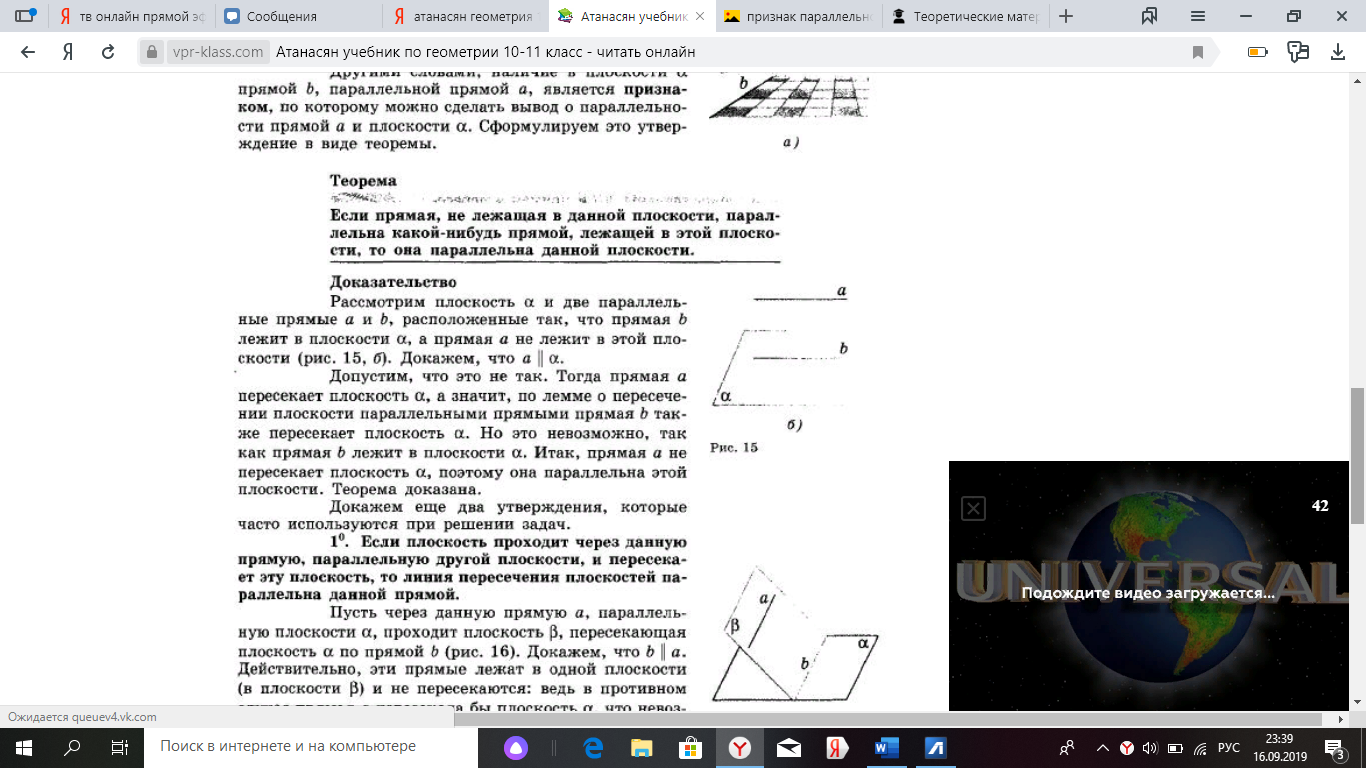
6. Оформление доказательства теоремы.

7. Усвоение формулировки теоремы.

1.Сформулируйте еще раз признак, по которому можно сделать вывод о параллельности прямой и плоскости:

если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

2.Сформулируйте признак в форме «если…, то...»:

Если дана плоскость, в которой лежит какая-то прямая а, параллельная прямой b, не лежащей в этой плоскости, то эта плоскость параллельна прямой b.

3.Раскидать слова из признака в произвольном порядке и попросить составить его.

8. Усвоение доказательства теоремы.

-Как мы доказывали данный признак?

-методом «от противного», мы предположили, что прямая пересекает плоскость.

-Есть 2 метод доказательства:

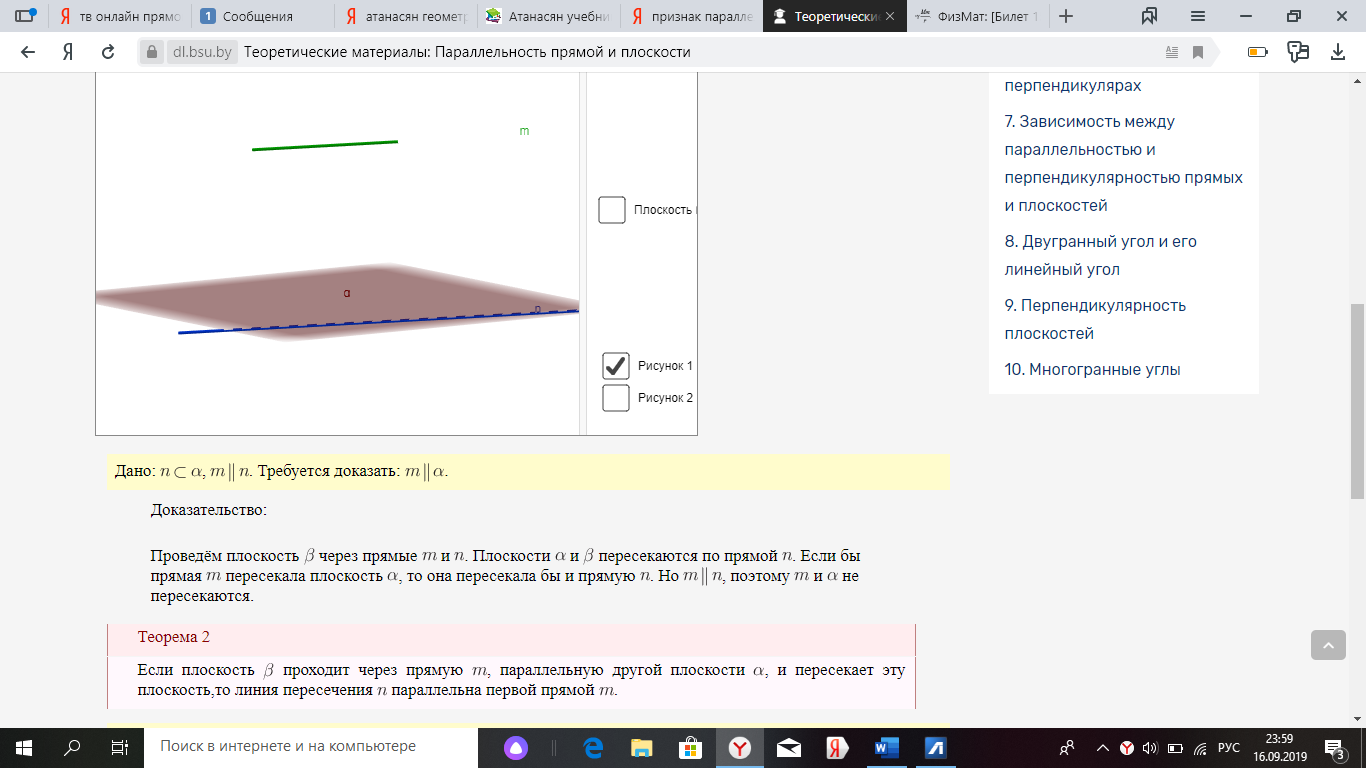
Докажите данный признак, если дана плоскость , прямая n – не лежащая в данной плоскости и прямая m – лежащая в ней.

9. Решение задач по применению теоремы.

Первичное осмысление и закрепление новых знаний.

1. В классной комнате, используя признак параллельности прямой и плоскости, укажите прямые и параллельные им плоскости.

2. Работаем в парах. Используя признак параллельности прямой и плоскости, укажите прямые и параллельные им плоскости на моделях куба или призмы.

3. Задачи на «воображаемое построение»: 1) через данную точку провести прямую параллельную данной плоскости;

2) через данную точку провести плоскость, параллельную данной прямой.

Задача 1:

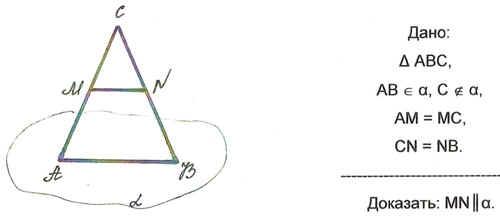
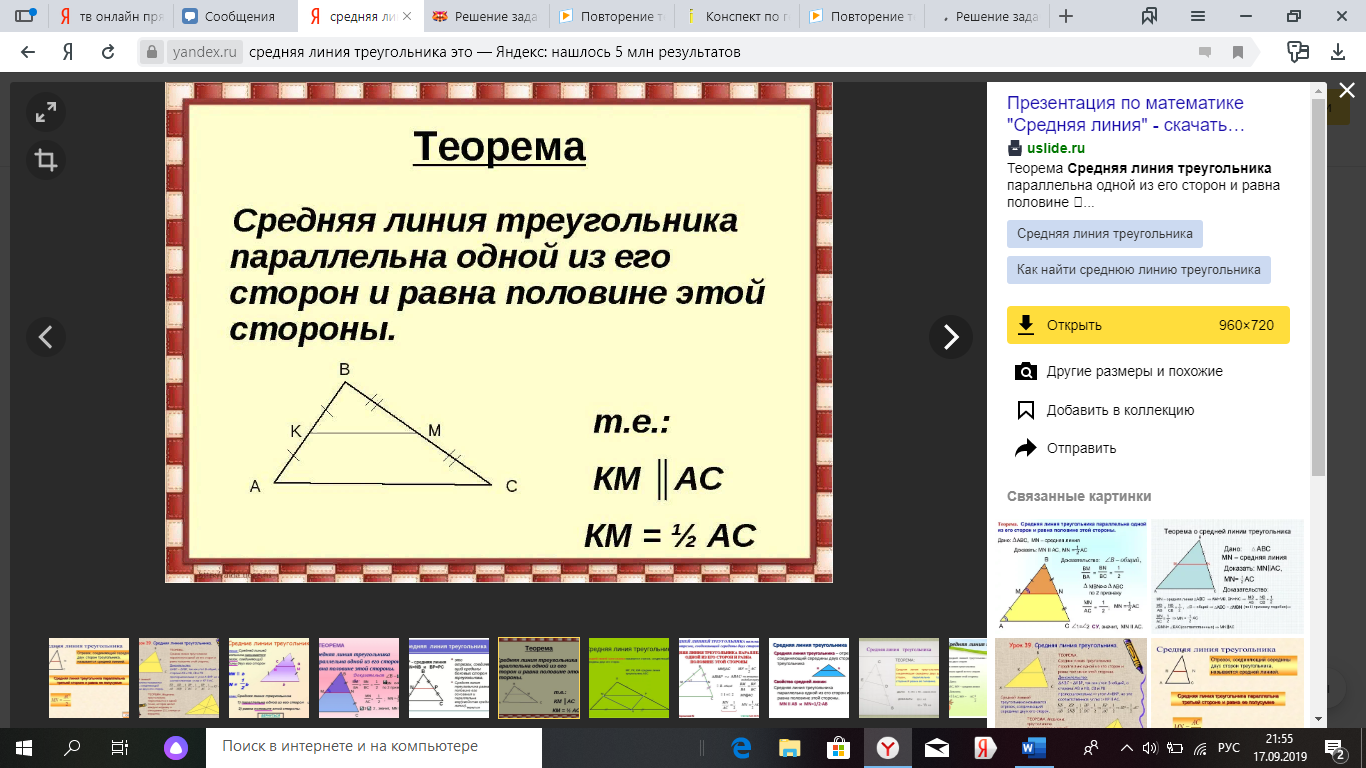
Доказательство

МN - средняя линия треугольника АВС, значит МN || АВ, АВ   a .

Таким образом, МN || a (по признаку параллельности прямой и плоскости).

Задача 2:

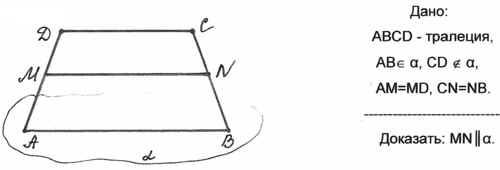
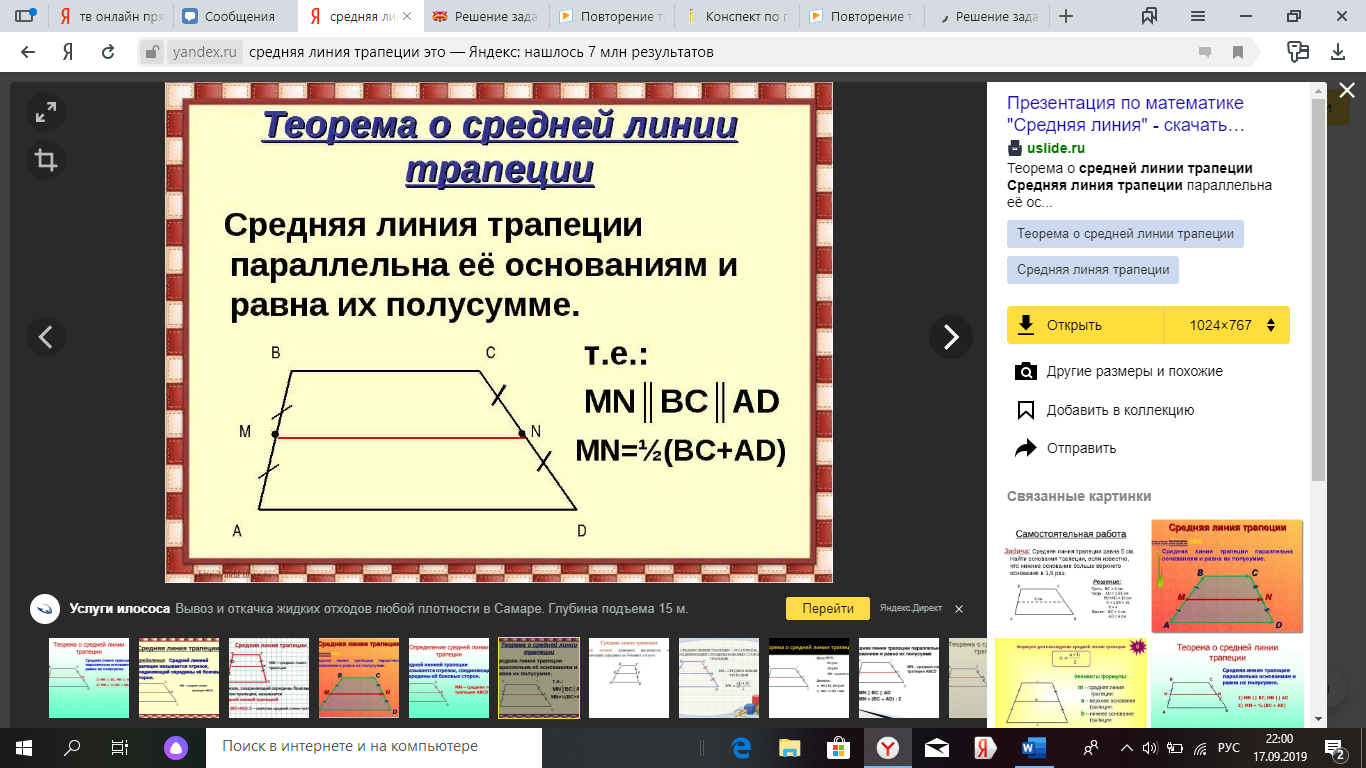
Доказательство

МN - средняя линия трапеции АВСD, значит МN || АВ; АВ   a (по условию),

Таким образом, МN || a (по признаку параллельности прямой и плоскости).

10. Контроль и оценка усвоения теоремы.

Ответить да/нет:

Знаете ли вы формулировку теоремы?

Умеете ли выделять условие и заключение теоремы?

Умеете строить чертеж?

Можете доказывать теорему?

Можете пользоваться этим признаком при решении задач?