Фонд оценочных средств по геометрии 8 класс
Контрольная работа№ 1. Четырехугольники
Контрольная работа № 2. Теорема Пифагора. Площадь
Контрольная работа № 3. Подобные треугольники
Контрольная работа № 4. Окружность
Контрольная работа № 5. Итоговая контрольная работа
Оценка контрольных работ
Ответ оценивается отметкой «5», если:
1) работа выполнена полностью;
2) в логических рассуждениях и обосновании решения нет пробелов и ошибок;
3) в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
1) работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
2)допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
1) допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
1) допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
| Контрольная работа № 1. Г-8. Вариант-1 № 1. Диагонали прямоугольника ABCD пересекаются в точке О, ∟АВО=360. Найдите угол AOD. № 2. Найдите углы прямоугольной трапеции, если один из его углов равен 200. № 3. Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма. № 4. В равнобедренной трапеции сумма углов при большем основании равна 960. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, АМ = 4 см. Найдите длину диагонали АD. | Контрольная работа № 1. Г-8. Вариант-2. № 1. Диагонали прямоугольника MNKP пересекаются в точке О, ∟MОN=640. Найдите угол OMP. № 2. Найдите углы равнобедренной трапеции, если один из его углов на 300 больше другого. № 3. Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см. Найдите стороны параллелограмма. № 4. В прямоугольной трапеции разность углов при одной из боковых сторон равна 480. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, длина диагонали АС равна 6 см. Найдите AМ, если точка М лежит на продолжении стороны AD. |
| Контрольная работа № 1. Г-8. Вариант-3. № 1. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма. № 2. Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4: 5. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна одной из его сторон. № 4. В трапеции ABCD диагональ BD перпендикулярна боковой стороне AB, ∟ADB = ∟BDC = 300. Найдите длину АD, если периметр трапеции равен 60 см. № 5*. В параллелограмме ABCD биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М2, М 1М2 = 8см. Найдите AD. | Контрольная работа № 1. Г – 8. Вариант – 4. 1. Периметр параллелограмма 60 см. Одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма. № 2. Угол между диагоналями прямоугольника равен 800. Найдите угол между диагональю и меньшей стороной прямоугольника. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна половине неперпендикулярной к ней стороны параллелограмма. № 4. В трапеции ABCD диагональ AС перпендикулярна боковой стороне CD и является биссектрисой угла А. Найдите длину АВ, если периметр трапеции равен 35 см, ∟D = 600. № 5*. В параллелограмме ABCD AD = 6 см. Биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М 2. Найдите М1М2.
|
|
|
|
| Контрольная работа № 2. Г-8 Вариант-1. № 1. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника. № 2. Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь этого треугольника. № 3. Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см. № 4*. В прямоугольной трапеции АВСК большая боковая сторона равна 3√2 см, угол К равен 450, а высота СН делит основание АК пополам. Найдите площадь трапеции.
| Контрольная работа № 2. Г-8 Вариант-2. № 1. Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше стороны. Найдите площадь треугольника. № 2. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь этого треугольника. № 3. Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр. № 4*. В прямоугольной трапеции АВСD большая боковая сторона равна 8 см, угол А равен 600, а высота ВН делит основание АD пополам. Найдите площадь трапеции. |
| Контрольная работа № 2. Г-8 Вариант-3. № 1. Смежные стороны параллелограмма равны 52 см и 30 см, а острый угол равен 300. Найдите площадь параллелограмма. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если А= 24 см, ВС = 16 см, ∟А= 45, ∟D=90 0. № 3. Дан треугольник АВС. На стороне АС отмечена точка К так, что АК = 6 см, КС = 9 см. Найдите площади треугольников АВК и СВК, если АВ = 13 см, ВС = 14 см. № 4*. Высота равностороннего треугольника равна 6 см. Найдите сумму расстояний от произвольной точки, взятой внутри этого треугольника, до его сторон. | Контрольная работа № 2. Г-8 Вариант-4. № 1.Высота ВК, проведенная к стороне АD параллелограмма АВСD, делит эту сторону на два отрезка АК = 7 см, КD = 15 см. Найдите площадь параллелограмма, если ∟А =450. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если ВС = 13 см, АD = 27 см, СD = 10см, ∟D = 300. № 3. Дан треугольник МКР. На стороне МК отмечена точка Т так, что МТ= 5 см, КТ = 10 см. Найдите площади треугольников МРТ и КРТ, если МР = 12 см, КР = 9 см. № 4*. В равностороннем треугольнике большая сторона составляет 75% суммы двух других. Точка М, принадлежащая этой стороне, является концом биссектрисы треугольника. Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см.
|
|
|
|
| Контрольная работа № 3. Г-8.
№ 1. Рисунок 1 Дано: ∟А = ∟В, СО = 4, DО = 6, АО = 5. С Найти: а) ОВ; б) АС : ВD; в) SAOC : SBOD. А О D
№ 2. В треугольнике АВС АВ = 4 см, ВС= 7 см, АС = 6 см, а в треугольнике МNК МК = 8 см, МN =12 см, КN = 14 см. Найдите углы треугольника МNК, если ∟А = 80, ∟В = 600. № 3. Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК ║АС, ВМ : АМ = 1: 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, А = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника АОD равна 45 см2.
| Контрольная работа №3. Г-8. Вариант-2. N
Найти: а) МК; б) РЕ : NК; в) SМЕР : SMKN.
M E K № 2. В ∆АВС АВ = 12 см, ВС = 18 см, ∟В = 700,а в ∆ МNК MN = 6 cм, NК = 9 см, ∟N= 700. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, ∟К = 600. № 3. Отрезки АВ и СD пересекаются в точке О так, что ∟АСО = =∟ВDО, АО : ОВ = 2 : 3. Найдите периметр треугольника АСО, если периметр треугольника ВОD равен 21 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, SAOD= 32 см2, S BOC = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см.
|
| Контрольная работа № 3. Г-8. Вариант-3. № 1. Рисунок 1. D B
ОВ = 5,1 см, ОD = 6,3 см. O Доказать: АС ║ВD.
в) SDBO : SAOC A C № 2. Диагонали ромба АВСD пересекаются в точке О, ВD = 16 см. На стороне АВ взята точка К так, что ОК ┴ АВ и ОК = 4√3 см. Найдите сторону ромба и второю диагональ. № 3. В выпуклом четырехугольнике АВСD АВ = 9 см, ВС = 8 см, СD = 16 см, АD = 6 см, ВD = 12 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике МNК с основанием МК, равным 10 см, МN= NК = 20 см. На стороне NК лежит точка А так, что АК : АN= 1 : 3. Найдите АМ. | Контрольная работа № 3. Г-8. Вариант-4.
Дано: ВD = 3,1 см, ВЕ = 4,2 см, ВА = 9,3 см, ВС = 12,6 см. D E
Найти: а) DЕ : АС; б) РABC : РDBE ; в) SDBE : SABC. A C № 2. Диагонали ромба АВСD пересекаются в точке О. На стороне АВ взята точка К так, что ОК ┴ АВ, АК = 2 см, ВК = 8 см. Найдите диагонали ромба. № 3. АВСD – выпуклый четырёхугольник, АВ = 6 см, ВС = 9 см, СD = 10 см, DА = 25 см, АС = 15 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике АВС АВ = ВС = 40 см, АС = 20 см. На стороне ВС отмечена точка Н так, что ВН : НС = 3 : 1. Найдите АН.
|
|
Контрольная работа № 4. Г-8. Вариант-1. № 1. Средние линии треугольника относятся как 2: 2: 4, а периметр треугольника равен 45 см. Найдите стороны треугольника. № 2. Медианы треугольника АВС пересекаются в точке О. Через точку О проведена прямая, параллельная стороне АС пересекающая стороны АВ и ВС в точках Е и F соответственно. Найдите ЕF, если сторона АС равна 15 см. № 3. В прямоугольном треугольнике АВС (∟С= 900) АС = 5 см, ВС = 5√3 см. Найдите угол В и гипотенузу АВ. № 4. В треугольнике АВС ∟А =α, ∟С =β, сторона ВС = 7 см, ВН-высота. Найдите АН. № 5. В трапеции АВСD продолжения боковых сторон пересекаются в точке К, причем точка В-середина отрезка АК. Найдите сумму оснований трапеции, если АD = 12 см. |
Контрольная работа №4. Г-8. Вариант-2. № 1. Средние линии треугольника относятся как 4: 5: 6, а периметр треугольника, образованного средними линиями, равен 30 см. Найдите средние линии треугольника. № 2. Медианы треугольника MNK пересекаются в точке О. Через точку О проведена прямая, параллельная стороне MK пересекающая стороны MN и NK в точках A и B соответственно. Найдите MK, если длина отрезка АB равна 12 см. №3. В прямоугольном треугольнике РКТ (∟Т= 900), РТ = 7√3 см, КТ= 7 см. Найдите угол К и гипотенузу КР. № 4. В треугольнике АВС ∟А =α, ∟С =β , высота ВН равна 4 см. Найдите АС. № 5. В трапеции MNKP продолжения боковых сторон пересекаются в точке E, причем EK=KP. Найдите разность оснований трапеции, если NK = 7 см. |
| Контрольная работа № 4. Г-8. Вариант-3. № 1. На стороне ВС треугольника АВС выбрана точка D так, что ВD: DС = 3:2, точка К – середина отрезка АВ, точка F–середина отрезка АD, КF =6 см, ∟АDС=1000. Найдите ВС и ∟АFК. № 2. В прямоугольном треугольнике АВС ∟С= 900, АС = 4 см, СВ = 4√3 см, СМ –медиана. Найдите угол ВСМ. № 3. В равнобедренной трапеции основания равны 8 см и 12 см, меньший угол равен α . Найдите периметр и площадь трапеции. № 4.В равнобедренном треугольнике АВС с основанием АС медианы пересекаются в точке О. Найдите площадь треугольника АВС, если ОА =13 см, ОВ = 10 см. № 5. В трапеции АВС (ВС ║АD) АВ ┴ ВD, ВD =2√5 , AD =2√10, СЕ – высота треугольника ВСD, а tg∟ECD= 3. Найдите ВЕ. | Контрольная работа № 4. Г-8. Вариант-4. № 1. На стороне АМ треугольника АВМ отмечена точка Н так, что АН: НЬ = 4:7; точка С – середина стороны АВ, точка О –середина стороны отрезка ВН, АМ = 22 см, ∟ВОС = 1050. Найдите СО и угол ВНМ. № 2. В прямоугольном треугольнике MNK ∟K= 90, KM = 6см, NК =6√3 см, КD- медиана. Найдите угол КDN. № 3. В равнобедренной трапеции боковая сторона равна 6 см, меньшее основание 10 см, а меньший угол α . Найдите площадь трапеции. № 4. В прямоугольном треугольнике АВС (∟С =900) медианы пересекаются в точке О, ОВ = 10 см, ВС = 12 см. Найдите гипотенузу треугольника. № 5. В трапеции АВСD ∟А =90, АС= 6√2, ВС=6, DЕ –высота треугольника АСD, tg∟ACD= 2. Найдите СЕ. |
| Контрольная работа № 5. Г-8. Вариант-1. № 1. АВ и АС- отрезки касательных, проведенных к окружности радиуса 9 см. Найдите длины отрезков АС и АО, если АВ = 12 см. № 2. Рисунок 1. Дано: ᵕАВ : ᵕВС = 11 : 12.
130O C № 3. Хорды MN и PK пересекаются точке E так, что ME =12 см, NE =3 см, PE=KE. Найдите PK. № 4.Окружность с центром в точке О радиусом 16 см описана около треугольника ABC так, что ∟OAB=300, ∟OCB=450. Найдите стороны AB и BC треугольника. | Контрольная работа № 5. Г-8. Вариант-2. № 1. MN и MK-отрезки касательных, проведенных к окружности радиуса 5 см. Найдите MN и MK, если МО= 13 см. № 2. Рисунок 1. Дано: ᵕАВ : ᵕАС = 5 : 3.
C O № 3. Хорды АВ и СD пересекаются точке F так, что АF =4 см, ВF =16 см, СF=DF. Найдите CD. № 4.Окружность с центром в точке О радиусом 12 см описана около треугольника MNK так, что ∟MON=1200, ∟NOK=900. Найдите стороны MN и NK треугольника. |
| Контрольная работа № 5. Г-8. Вариант-3. № 1. В треугольник вписана окружность так, что три из шести получившихся отрезков касательных равны 3 см,4 см,5 см. Определите вид треугольника № 2. Точки А и В делят окружность с центром О на дуги АВМ и АСВ так, что дуга АСВ на 600 меньше дуги АМВ. АМ- диаметр окружности. Найдите углы АМВ, АВМ, АСВ. № 3. Хорды АВ и СD пересекаются в точке Е так, что АЕ=3 см, ВЕ=36 см, СЕ: DЕ =3:4. Найдите СD и наименьшее значение радиуса этой окружности. № 4. В равнобедренном треугольнике боковая сторона равна 10 см, а биссектриса, проведенная к основанию 8 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника.
| Контрольная работа № 5. Г-8. Вариант-4. № 1. В прямоугольный треугольник вписана окружность радиусом 2 см так, что один из получившихся отрезков касательных равен 4 см. Найдите стороны треугольника, если его периметр равен 24 см. № 2.Точки Е и Н делят окружность с центром О на дуги ЕАН и ЕКН так, что дуга ЕКН на 900 меньше дуги ЕАН, ЕА- диаметр окружности. Найдите углы ЕКА, ЕАН, ЕКН. № 3. Хорды МN и РК пересекаются в точке А так, что МА= 3 см, NА= 16 см, РА: КА= 1: 3. Найдите РК и наименьшее значение радиуса этой окружности. № 4. В равнобедренном треугольнике основание равно 10 см, а высота, Проведенная к ней, 12 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника. |
Ответы.
|
|
| № 1 | № 2 | № 3 | № 4 | № 5 |
| Контрольная работа № 1. | Вариант-1 | ∟АОD=72 | 900 , 900, 1600, 200 | 5см, 10см, 5см, 10см | 480, 480, 1320, 1320 | DВ=6см |
| Вариант-2 | ∟ОМР=32 | 750, 1050, 1050, 750 | 5см, 15см, 5см, 15см | 660, 1140, 900, 900 | АМ=3см | |
| Вариант-3 | 10см, 15см, 10см, 15см | 800 | 450, 1350 450,1350 | AD=24см | AD=8см | |
| Вариант-4 | 18см, 12см, 18см, 12см | 500 | 300, 300, 1500, 1500 | АВ= 7см | М1 М2 =6см | |
| Контрольная работа № 2. | Вариант-1 | 24см2 | 10см, 24см2 | Р=4√41см, S= 40cм2 | S АВСК= 13,5см2 | - |
| Вариант-2 | 24см2 | 5см, 30см2 | Р=4√61см, S= 60cм2 | S АВСD= 24√3см2 | - | |
| Вариант-3 | 780cм2 | SABCD = 160cм2 | SABK =33,6см2, SCBK =50,4см2 | 6см | - | |
| Вариант-4 | 154см2 | SABCD = 100cм2 | SKPT=36см2, SMPT =18см2 | 3см | - | |
| Контрольная работа № 3. | Вариант-1 | а) 7,5; б) в) | 800, 600,400 | 5см | S = 5см2 | - |
| Вариант-2 | а) 9; б) в) | AC=14см, ∟С=600 | 14см | 5см2 | - | |
| Вариант-3 | а) | АВ=6см; АС= 16√3 | - | 10см | - | |
| Вариант-4 | а) | АС=4√5; ВD=8√5 | - | 20см |
| |
| Контрольная работа № 5. | Вариант-1 | 15см | ∟ВСА=550, ∟ВАС=600 | РЕ=6см, РК= 12см | АВ=16√3см, ВС= 16√2см | - |
| Вариант-2 | 12см | ∟ВОС=1200, ∟АВС=450 | СF=8см, СD=16см | МN=12√3см; NК=12√2см | - | |
| Вариант-3 | 6см, 8см, 10 см | ∟АМВ=600, ∟АВМ=900, ∟ АСВ=1050
| СD=21см, 19,5см | 3см, 6,25см |
| |
| Вариант-4 | 6см, 8см, 10см | ∟ЕКА=90, ∟ЕАН=670 30١, ∟ЕКН=1120 30١ | РК=16см, 9,5см | 3см, 7см |
|

 Получите свидетельство
Получите свидетельство Вход
Вход



 Вариант-1. B
Вариант-1. B № 1. Рисунок 1. P
№ 1. Рисунок 1. P Дано: РЕ ║NК, МР = 8, МN = 12, МЕ = 6.
Дано: РЕ ║NК, МР = 8, МN = 12, МЕ = 6.

 Дано: АО = 6,8 см, СО = 8,4 см,
Дано: АО = 6,8 см, СО = 8,4 см,  № 1. Рисунок 1. B
№ 1. Рисунок 1. B Доказать: DЕ ║АС.
Доказать: DЕ ║АС. Найдите ∟ВСА, ∟ВАС.
Найдите ∟ВСА, ∟ВАС.
 B A
B A
 A B
A B
 60O
60O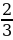 ;
;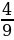
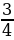 ; б)
; б) 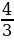 ; в)
; в) 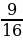
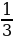 ; б) 3; в)
; б) 3; в) 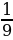









 Методические рекомендации по организации оценочных процедур по геометрии для 8 класса (84.37 KB)
Методические рекомендации по организации оценочных процедур по геометрии для 8 класса (84.37 KB)
 0
0 238
238 0
0 Нравится
0
Нравится
0


