Метод решения неоднородного тригонометрического уравнения

Метод решения неоднородного тригонометрического уравнения

Подготовила: учитель математики первой квалификационной категории Уткина Елена Николаевна 2016 год

Листок настроения.

В начале урока у первого солнышка нарисовать свое настроение ,

в конце – у второго.

А. Энштейн говорил : «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по - моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».

Устный счёт

Выберите верное решение уравнения:

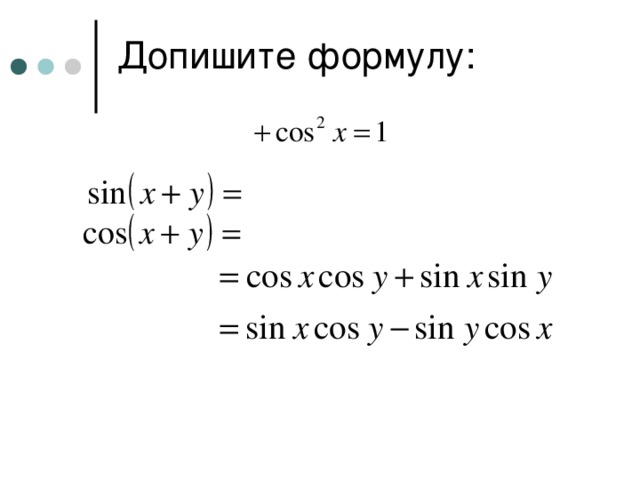
Допишите формулу:

С помощью каких методов решаются данные уравнения?

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

решение

Уравнение вида

называется однородным тригонометрическим уравнением

второй степени.

Т. К.

Метод замены переменной

Уравнение принимает вид

Уравнение вида

называется однородным тригонометрическим уравнением первой степени.

т. к.

Применение формул синус и косинус суммы и разности аргументов

Метод разложения на множители

Если то преобразуем к

виду либо

Задача сводится к совокупности решений

Для преобразования уравнений вида

воспользуемся формулой синуса суммы

Разделим обе части уравнения на

Алгоритм решения уравнений вида

• Найдём число такое, что

• Выполняем замену
• Получаем уравнение вида
• Решение уравнения

Решите уравнение

1 группа

2 группа

3 группа

Алгоритм решения:

1)

2)

3)

4)

Работа в группах.

1 группа

Решите уравнение:

Ответ:

2 группа

3 группа

Работа в группах.

2 группа

Решите уравнение:

Ответ:

1 группа

3 группа

Работа в группах .

3 группа

Решите уравнение:

Ответ:

1 группа

2 группа

Домашнее задание

• № 30.15(в)
• № 30.16(в)
• № 30.17(а, г)

На листе настроения нарисуйте

своё настроение в конце урока

Используя 10 балльную шкалу,

оцените свои знания и умения

• по использованию

метода решения неоднородного тригонометрического уравнения

• степень полезности урока