Методическая разработка по математике на тему «Формирование общих компетенций на учебных занятиях по дисциплине «Математика»

Введение

Молодому специалисту, вступающему в самостоятельную жизнь в условиях современного рынка труда, необходимо быть эффективным, конкурентоспособным работником. Он должен быть творческим, самостоятельным, ответственным, коммуникабельным человеком, способным решать проблемы личные и коллектива. Все эти качества можно успешно формировать, используя компетентностный подход в обучении математике, что является одним из личностных и социальных смыслов образования.

Следует различать понятия "компетенция" и "компетентность". В. Хуторской предлагает следующие определения.

Компетенция – включает совокупность взаимосвязанных качеств личности (знаний, умений, навыков, способов деятельности), задаваемых по отношению к определенному кругу предметов и процессов, и необходимых для качественной продуктивной деятельности по отношению к ним.

Компетентность – владение, обладание человеком соответствующей компетенцией, включающей его личностное отношение к ней и предмету деятельности.

Выпускник должен обладать общими компетенциями:

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

ОК 2. Анализировать социально-экономические и политические проблемы и процессы, использовать методы гуманитарно-социологических наук в различных видах профессиональной и социальной деятельности.

ОК 3. Организовывать свою собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 4. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.

ОК 5. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.

ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями.

ОК 7. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ОК 8. Быть готовым к смене технологий в профессиональной деятельности.

ОК 9. Уважительно и бережно относиться к историческому наследию и культурным традициям, толерантно воспринимать социальные и культурные традиции.

ОК 10. Соблюдать правила техники безопасности, нести ответственность за организацию мероприятий по обеспечению безопасности труда.

На своих учебных занятиях, используя компетентностный подход, стараюсь наполнить математическое образование знаниями, умениями и навыками, связанными с личным опытом и потребностями обучающегося с тем, чтобы он мог осуществлять продуктивную и осознанную деятельность по отношению к объектам реальной действительности.

Рассмотрим несколько фрагментов учебных занятий по математике.

Пример 1: Занятие на закрепление знаний по теме «Объемы тел»

Раздаю обучающимся (одну модель на стол) модели тел вращения (шар, цилиндр, конус) и многогранников (призмы, пирамиды). Обучающимся предлагаю дать характеристику предложенных тел, дать их определение, назвать отличительные свойства тела. Далее предлагаю рассмотреть слайды с изображением различных предметов, носящих форму пространственных фигур и по данным вычислить объемы тел.

Пример 2: Занятие усвоения новых знаний по теме: «Тригонометрические уравнения, сводящиеся к квадратным»

Проведя актуализацию знаний обучающихся по решению простейших тригонометрических уравнений, записываю на доске тригонометрическое уравнение, сводящееся к квадратному и ставлю проблему -как решить данное тригонометрическое уравнение, например. Стараюсь, чтобы на моих занятиях обучающиеся добывали нужную информацию, используя доступные источники (справочники, учебники, словари, ресурсы Internet) и учу их "говорить".

Пример 3: Занятие по теме: «Пирамида»

При актуализации знаний применяю принцип: "ассоциаций", т. е. на доске написано слово "Пирамида", а обучающиеся высказывают свои ассоциации к этому термину, затем дают определение (ребро, высота, площади полной поверхности. . . )

На обобщающих учебных занятиях, разбиваю обучающихся на группы, которым выдается комплект заданий.

Полную информацию смотрите в файле. 

Министерство образования и науки Челябинской области

государственное бюджетное профессиональное образовательное учреждение

«Южно-Уральский многопрофильный колледж»

Методическая разработка

Формирование общих компетенций на учебных занятиях по дисциплине «Математика»

О Д О Б Р Е Н О

Цикловой методической комиссией

естественнонаучных дисциплин

Протокол № 5

« 26 » января 2016 г.

Председатель ЦМК

_____________О.Н. Суханова

Составитель: М.А. Вуйлова, методист, преподаватель математики высшей категории ГБПОУ «Южно-Уральский многопрофильный колледж»

Рецензент: Е.А.Кондратьева, преподаватель математики высшей категории ГБПОУ «Южно-Уральский многопрофильный колледж»

Введение

Молодому специалисту, вступающему в самостоятельную жизнь в условиях современного рынка труда , необходимо быть эффективным, конкурентоспособным работником. Он должен быть творческим, самостоятельным, ответственным, коммуникабельным человеком, способным решать проблемы личные и коллектива. Все эти качества можно успешно формировать, используя компетентностный подход в обучении математике, что является одним из личностных и социальных смыслов образования.

Следует различать понятия "компетенция" и "компетентность". В.Хуторской предлагает следующие определения.

Компетенция – включает совокупность взаимосвязанных качеств личности (знаний, умений, навыков, способов деятельности), задаваемых по отношению к определенному кругу предметов и процессов, и необходимых для качественной продуктивной деятельности по отношению к ним.

Компетентность – владение, обладание человеком соответствующей компетенцией, включающей его личностное отношение к ней и предмету деятельности.

Выпускник должен обладать общими компетенциями:

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

ОК 2. Анализировать социально-экономические и политические проблемы и процессы, использовать методы гуманитарно-социологических наук в различных видах профессиональной и социальной деятельности.

ОК 3. Организовывать свою собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 4. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.

ОК 5. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.

ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями.

ОК 7. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ОК 8. Быть готовым к смене технологий в профессиональной деятельности.

ОК 9. Уважительно и бережно относиться к историческому наследию и культурным традициям, толерантно воспринимать социальные и культурные традиции.

ОК 10. Соблюдать правила техники безопасности, нести ответственность за организацию мероприятий по обеспечению безопасности труда.

На своих учебных занятиях, используя компетентностный подход, стараюсь наполнить математическое образование знаниями, умениями и навыками, связанными с личным опытом и потребностями обучающегося с тем, чтобы он мог осуществлять продуктивную и осознанную деятельность по отношению к объектам реальной действительности.

Рассмотрим несколько фрагментов учебных занятий по математике.

Пример 1: Занятие на закрепление знаний по теме «Объемы тел»

Раздаю обучающимся ( одну модель на стол) модели тел вращения (шар, цилиндр, конус) и многогранников (призмы, пирамиды). Обучающимся предлагаю дать характеристику предложенных тел, дать их определение, назвать отличительные свойства тела. Далее предлагаю рассмотреть слайды с изображением различных предметов, носящих форму пространственных фигур и по данным вычислить объемы тел.

Пример 2: Занятие усвоения новых знаний по теме: «Тригонометрические уравнения, сводящиеся к квадратным»

Проведя актуализацию знаний обучающихся по решению простейших тригонометрических уравнений, записываю на доске тригонометрическое уравнение, сводящееся к квадратному и ставлю проблему -как решить данное тригонометрическое уравнение, например. Стараюсь, чтобы на моих занятиях обучающиеся добывали нужную информацию, используя доступные источники (справочники, учебники, словари, ресурсы Internet) и учу их "говорить".

Пример 3: Занятие по теме: «Пирамида»

При актуализации знаний применяю принцип: "ассоциаций", т. е. на доске написано слово "Пирамида", а обучающиеся высказывают свои ассоциации к этому термину, затем дают определение (ребро, высота, площади полной поверхности...)

На обобщающих учебных занятиях, разбиваю обучающихся на группы, которым выдается комплект заданий.

Та группа, которая быстрее решит все задания выигрывает. Каждый участник группы должен отчитаться о проделанной им работе. Работу каждого участника оценивает вся группа (составляя группу, учитываю, что в группах должно быть одинаковое количество "сильных" и "слабых" обучающихся, что силы групп были одинаковыми).

Пример 4: Этап рефлексии на занятии по теме «Призма».

В конце занятия каждому обучающемуся выдаются лист с нижеследующими вопросами

Поставьте «+» или «-» напротив каждого утверждения:

Я знаю определение призмы

Я знаю элементы призмы

Я знаю смогу отличить призму от других геометрических пространственных фигур

Я смогу объяснить отсутствующему на занятии, как построить призму и что это такое

Я знаю, какие тела называются многогранниками

Я знаю, почему призма относится к многогранникам

Я знаю, где применяется призма в повседневной жизни

Продолжите предложение:

Мое настроение на занятии …

1.Мне понравилось…

2.Мне не понравилось….

Оцените свою деятельность на занятии по пятибалльной шкале

Пример 5: на занятиях по математике я частично способствую формированию профессиональных компетенций, к примеру:

1) Необходимо на даче установить резервуар для воды емкостью в 10 м3 на площади размером 2,5 м × 1,75 м, служащей для него дном. Высота резервуара неизвестна.

2) Железнодорожная насыпь дана в разрезе на рисунке; размеры указаны в метрах. Найти, сколько кубических метров земли приходится на 1 км насыпи.

3) Цилиндрический паровой котел имеет 0,7 м в диаметре; длина его равна 3,8 м . Как велико давление на полную поверхность котла, если на 1см2 пар давит с силой в 10 кг

4) Сколько тонн нефти перевезет железнодорожный состав, состоящий из 40 наливных вагонов, имеющих длину 12 м, диаметр 3 м, если 1м3 нефти весит 800 кг.

5) Цилиндрическая цистерна, диаметр основания которой 3 м, а длина 4 м, заполнена дизельным топливом на 2/3 своего объема. Сколько тонн дизельного топлива содержится в цистерне, если его плотность 850 кг/м3?

6) Стрелочный перевод наклонен к плоскости железнодорожного полотна под углом 45°. Найти проекцию стрелочного перевода на плоскость железнодорожного полотна, если длина стрелки равна 80 см.

Это несколько примеров из моей практики, которые позволяют слегка приоткрыть "завесу" того, как я формирую на своих уроках ОК.

При проведении недели математики стараюсь составлять задания - викторины (в шуточной форме, требующие логического мышления), олимпиады так чтобы каждый обучающийся в группе мог поучаствовать. Стимулирую призовыми местами, призами, грамотами.

Прививаю навыки самостоятельной, творческой работы. Практически на каждом занятии обучающиеся выполняют самостоятельную работу, используя индивидуальные карточки разного уровня, чтобы обучающиеся могли выполнить задания на ту оценку, на которую они претендуют), тесты (при проведении тестов я использую на занятиях взаимоконтроль в парах: после написания теста пара меняется работами, Обучающийся самостоятельно проверяет работу товарища и выставляет оценку).

На своих занятиях стараюсь использовать игровую форму и создавать проблемную ситуацию. Карточки я составляю в 3-6 вариантах по 3 уровням усвоения. Это могут быть и тесты, и практические работы.

Обучающиеся на протяжении учебного года готовят презентации, рефераты, доклады, сообщения на различные математические темы.

Стараюсь, учить обучающихся грамотной математической речи как письменной, так и устной для этого провожу математические диктанты.

Прививаю навыки самоконтроля и взаимоконтроля ( особенно на уроках геометрии). Работая в мини- группах обучающиеся оценивают свою работу и работу товарищей. Так как этому уделяется внимание в течение учебного года, то ребята привыкают высказывать свое мнение, и адекватно оценивать себя и других.

В конце занятия отслеживаю рефлексию и самооценку.

В результате обучающиеся:

• используют знания, умения и навыки, полученные на занятиях по математике в практической деятельности;

• учатся ставить цели и планировать деятельность по их достижению;

• осваивают коммуникативный, аналитический, творческий типы деятельности;

• приобретают навыки работы со справочной литературой;

• адекватно оценивают деятельность товарищей и свою;

• меняют свое поведение в коллективе: прислушиваются к мнению другого человека и без боязни высказывают свое собственное мнение.

У обучающихся формируется представление о математике как о предмете, где каждому есть возможность выразиться.

На своих занятиях я способствую развитию таких качеств личности, как готовность и способность нести личную ответственность, как за собственное благополучие, так и за благополучие общества.

Учебное занятие по дисциплине ОДП. 10 «Математика» по специальности 21.02.05 «Земельно-имущественные отношения»

Тема: Вычисление объемов тел вращения.

Цель: развитие умения применять теоретические знания в решении задач практического и профессионального содержания.

Задачи:

Образовательная: формировать навыки применения формул объёмов тел вращения при решении задач практического содержания.

Развивающая: уметь логически мыслить, развить познавательный интерес; усилить мотивацию интереса к изучаемой дисциплине.

Воспитательная: воспитывать стремление достигать поставленную цель; чувство уверенности в себе, умение работать в коллективе.

Работа над формированием ОК:

ОК 2. Анализировать социально-экономические и политические проблемы и процессы, использовать методы гуманитарно-социологических наук в различных видах профессиональной и социальной деятельности.

ОК 4. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.

ОК 5. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.

ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями.

Вид учебного занятия: закрепление изученного материала.

Формы работы обучающихся: фронтальная и индивидуальная.

Оборудование: модели конусов, цилиндров, усечённых конусов, контрольные карты, тесты.

Оформление доски: запись даты, темы урока, высказывания о математике, девиза.

Ход учебного занятия

Девиз:
«Искра знаний возгорается в том,
кто достигнет понимания собственными силами».

— Тема нашего занятия «Вычисление объемов тел вращения». Из названия темы сформулируйте цель. Значит, что в конце урока результат для каждого из вас будет.....?

— Наша совместная работа будет строиться так. Перед собой вы видите контрольный талон, куда вы будете ставить себе оценки за выполненную работу, а затем мы выведем с вами итоговую оценку за занятие. Во время занятия за активное участие, верные ответы вы будете получать жетоны, которые в конце занятия превратятся в оценку.

— Тела вращения встречаются практически в каждой сфере деятельности человека. Даже, казалось бы, не имеющей ничего общего с геометрией живописи тела вращения становятся объектами пристального внимания художников. Знаете ли вы, что знаменитый художник Мориц Эшер изображал практически всегда геометрические фигуры. Когда у Эшера спросили, почему среди его картин преобладают геометрические фигуры, он ответил, что с помощью этих фигур ему легче представить человеческую сущность: будь это человек острый как куб или же мягкий как, например, шар. «Каждый человек может найти в моих картинах что-то для себя», - говорил Мориц. «Что же касается сферических форм, то разве сама Вселенная не состоит из сфер?». Или вот вам другая информация к размышлению. По статистике на Земле ежегодно гибнет от разрядов молний 6 человек на 1000000 жителей (чаще в южных странах). Этого бы не случалось, если бы везде были громоотводы, так как образуется конус безопасности. Чем выше громоотвод, тем больше объем такого конуса.

— У всех на столах лежат тела вращения, но это не обычные тела – тела, с которыми вы встречаетесь дома, в окружающей нас среде.(стакан, колпачок, шарик…) Возьмите в руки эти фигуры и расскажите, что вы чувствуете, опишите свои ощущения. (дети высказываются) Действительно, это фигуры, которые несут свои какие-либо ощущения, но их всех объединяет то, что они занимают объем в пространстве.

— Сегодня на уроке мы будем работать с телами вращения, а точнее с их объемами. Зачем нам нужно уметь вычислять объемы тел? Дайте, пожалуйста, развернутый ответ.

Фронтальный опрос. Без каких знаний, мы результата в работе не добьемся?

 — Расскажите мне о них с геометрической точки зрения:

а) Какие тела вращения вам известны?

б) Какая фигура называется цилиндром?

в) Что является осевым сечение конуса?

г) Какая фигура называется шаром?

Работа у интерактивной доски.

— Сегодня нам на уроке понадобятся еще формулы для вычисления объемов тел вращения. Но вот проблема, пока я готовила урок, буквы в формулах разбежались и вот, что получилось. Вы мне поможете их собрать?

— Мы с вами повторили основные теоретические моменты, а теперь давайте попробуем наши знания применить на практике, выполнив задания – тесты. Вашему вниманию предлагаю тест, состоящий из двух вариантов и пяти заданий, а также предлагается контрольный талон, в котором вы подписываете Ф.И. и вычеркиваете ту буковку, под которой стоит найденный вами ответ.

Тесты.

1вариант.

1.Найдите объем цилиндра с высотой, равной 3см и диаметром основания – 6см.

б)9п см³; е)36п см³; э)27п см³ и)18п см³; д)54п см³.

 2. Диагональ осевого сечения цилиндра составляет с плоскостью основания цилиндра угол 60⁰ и равна 4 см. Найдите объем цилиндра , если высота равна 5см.

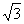
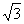а)16п см³ ; п)16см³; в)32п см³ й)5псм³; ц)16псм³.

3.Высота цилиндра равна 4 см, площадь основания - 18п см² Найдите объем цилиндра.

м)9п см³; б)31,5 см³, в)21п см³, к)63п см³, л)72п см³.

4. Найдите объем конуса , осевое сечение которого представляет собой равнобедренный прямоугольный треугольник с гипотенузой , равной 6см и высотой 3 см..

р) 18псм³, е)18п см³, у)6п см³, г)54псм³, о)6псм³.

 5.Найдите объем конуса , полученного в результате вращения вокруг большего катета, равного 8см прямоугольного треугольника с гипотенузой , равной 10 см.

з)18псм³, ш)108п см³, в)154псм³, р)96п см³ д)6п см³.

2 вариант.

1.Найдите объем цилиндра с высотой, равной 6см и диаметром основания – 4см.

б)9п см³; е)36п см³; э)24п см³ и)18п см³; д)54п см³.

2. Диагональ осевого сечения цилиндра составляет с плоскостью основания цилиндра угол 60⁰ и равна 8 см. Найдите объем цилиндра, если высота равна 4см.

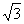
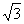а)16п см³ ; п)16см³; в)32п см³ й)16псм³; ц)16псм³.

3.Высота цилиндра равна 3 см, площадь основания - 17п см² Найдите объем цилиндра.

м)9п см³; б)31,5 см³, в)21п см³, к)63п см³, л)51п см³.

4. Найдите объем конуса , осевое сечение которого представляет собой равнобедренный прямоугольный треугольник с гипотенузой , равной 8см и высотой 3 см..

р) 18псм³, е)32п см³, у)6п см³, г)54псм³, о)6псм³.

  5.Найдите объем конуса, полученного в результате вращения вокруг меньшего катета, равного 6 см прямоугольного треугольника с гипотенузой , равной 10 см.

з)18псм³, ш)108п см³, в)154псм³, р)128п см³ д)6п см³.

Талон ответов: Э й л е р

Контрольный талон к тесту. Ф.И. студента

Оценка: если выполнены все пять заданий- "5"; если выполнено четыре задания- "4"; если выполнено три задания - "3".

Сообщение обучающегося о научном пути математика 18 века Эйлера.

2-3 мин.

Слово преподавателя. Практическая геометрия у древних народов

— Практическое применение геометрии начинается с древних времён. Египтяне использовали эту науку в различных хозяйственных работах, при сооружении оросительных каналов, грандиозных храмов и пирамид, при высечении из гранита знаменитых сфинксов и т.п. Содержащиеся в дошедших до нас папирусах геометрические сведения и задачи почти все относятся к вычислению площадей и объемов. В них нет никаких указаний на способы вывода тех правил, которыми пользовались египтяне для вычисления длин, площадей и объёмов; часто употреблялись правила приближённых подсчётов. Высшим достижением египетской геометрии следует считать точное вычисление объёма усечённого конуса, содержащееся в «Московском папирусе».

Геометрия и современность

— Велика роль геометрии и в нашем современном мире. В своей практической деятельности человек часто встречается с необходимостью вычисления объёмов, например, при изготовлении каких-либо деталей или при строительстве различных сооружений. Многие строительные объекты, детали конструкций и другие предметы имеют форму геометрических тел: параллелепипедов, призм, цилиндров, шаров

— Вот и мы попробуем с вами найти объемы не в простых геометрических задачах, которые направлены на закрепление формул и теоретических знаний, а в задачах, несущих практический характер.

Решение задач практического содержания

Задача № 1. Вы руководитель предприятия. Поставщик, указывая на кучу угля, имеющую коническую форму, предлагает вам вывезти ее, утверждая, что в ней такое- то количество тонн угля. Вы можете за раз вывести 26 т угля. Какое минимальное количество рейсов вам нужно сделать, если известно, что высота кучи 20 м, ее диаметр 50 м, у плотность угля 1,7 * 10³кг\м³.

Задача № 2. Хозяйка пришла в магазин, чтобы купить банку для крупы. Перед ней стал выбор какую банку купить: которая из двух банок вместительнее – правая, широкая или левая, втрое более высокая, но вдвое более узкая?

Задача № 3. Сколько тонн природного газа может перевезти поезд, имеющий в своём составе 15 цистерн, если диаметр котла каждой 3м, а длина 10,8 м, а плотность газа составляет 1,2 кг/м³?

Задача № 4. Радиус цилиндрического куска мыла уменьшился на 10%, а длина на 20%. Какой процент мыла использовали?

Решение: Пусть кусок мыла имеет размеры R, H. то V=πR²H.

Использованное мыло имеет размеры 0,9R; 0,8H, то

V₁=π·(0,9R)²·0,8H= π·0,81R²·0,8H≈0,65 πR²H

Значит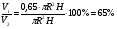
Следовательно, использовали 35% мыла. 

Вывод по задачам:

• Какие вопросы возникли при решении задач?

• Какой метод решения в 1 задаче?

• Какие теоретические основы легли в решение данной задачи?

— А теперь индивидуальные задания. На листочках самостоятельно сформулируйте условие задачи, которая решался бы в профессиональной деятельности при помощи математических знаний. Тут же напишите способ решения. Какие способы решения вы знаете? Задание понятно? Приступаем к работе.

Критерии оценивания данного вида работы:

• Если ваша задача предполагает решение с помощью арифметических вычислений, задача на «3».

• Если ваша задача предполагает решение на математическом языке — «4»

• Если ваша задача предполагает решение с помощью геометрии — «5»

Домашнее задание:

— Существует старинная легенда восточных народов, рассказанная А.С. Пушкиным в «Скупом рыцаре» и вот отрывок из нее хочу вам зачитать:

«….Читал я где – то,

Что царь однажды воинам своим

Велел снести земли по горсти в кучу,

И гордый холм возвысился, -и царь

Мог с вышины с весельем озирать

И дол, покрытый белыми шатрами ,

И море , где бежали корабли.»

(А.С. Пушкин «Скупой рыцарь»)

О какой геометрической фигуре здесь идет речь? (ответ)

Вот на этой поэтической ноте мы и перейдем с вами к домашнему заданию.

1 Авиационная бомба среднего калибра дает при взрыве воронку диаметром 6м и глубиной 2м. Какое количество земли (по массе) выбрасывает эта бомба, если 1м³ имеет массу 1650кг?

2. Предположив, что численность войска составляет 100 000 человек, объем горсти равен 0,2дм³,а угол при основании холма 45⁰, найдите объем и высоту конуса,

Выставление оценок за урок.

Контрольная карта Ф. И. обучающегося____________________

Вопросы для рефлексии.
1. Достиг ли я цели, поставленной в начале урока?

УФФФ, кажется, да кто бы сомневался нужно поработать еще

2. Задания были по моим силам?

Да и я сработал на все 100% У меня остались силы еще для 2 уроков математики.