Факультативное занятие по математике в 11 классе по теме
«Способы решения иррациональных уравнений»
Цели и задачи: систематизировать, расширить и углубить знания и умения учащихся в применении различных методов при решении иррациональных уравнений; формировать навыки анализа полученной информации.
Иррациональные уравнения часто встречаются в заданиях ЕГЭ по математике, т.к. с их помощью легко диагностируются знания выпускником таких понятий как область определения и равносильные преобразования.
Определение: уравнения, в которых переменная содержится под знаком корня, называются иррациональными.
Решить уравнение – это значит найти все такие значения переменной, при подстановке которых в уравнение оно превращается в верное равенство, либо доказать, что таких значений переменной не существует.
1). Решите уравнения:
а) 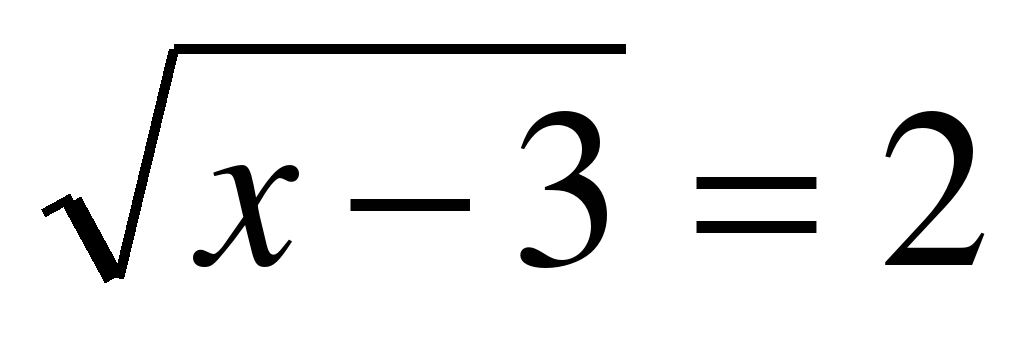 , х – 3 = 4, х = 7. Ответ: 7
, х – 3 = 4, х = 7. Ответ: 7
б) 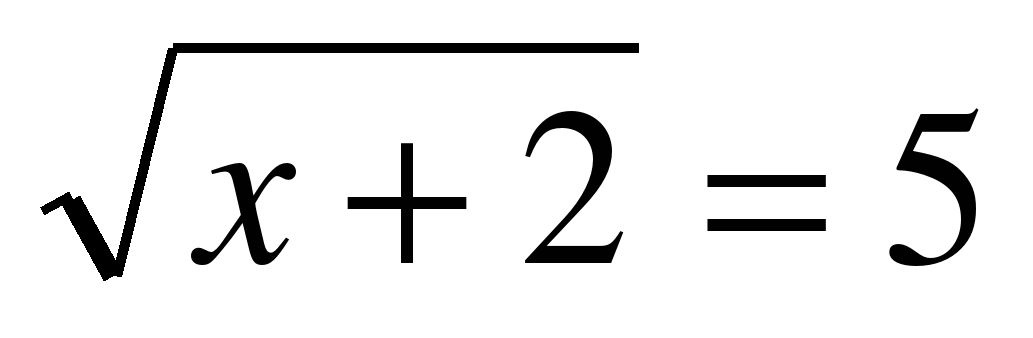 , х + 2 = 25, х = 23. Ответ: 23
, х + 2 = 25, х = 23. Ответ: 23
в) 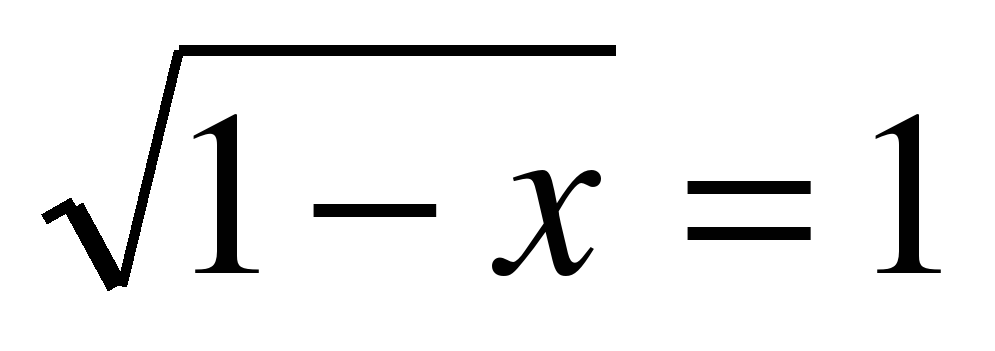 , 1 – х = 1, х = 0. Ответ: 0
, 1 – х = 1, х = 0. Ответ: 0
Вывод 1. Решение иррациональных уравнений сводится к переходу от иррационального уравнения к рациональному путем возведения в степень обеих частей уравнения.
2). Решите уравнения:
а) 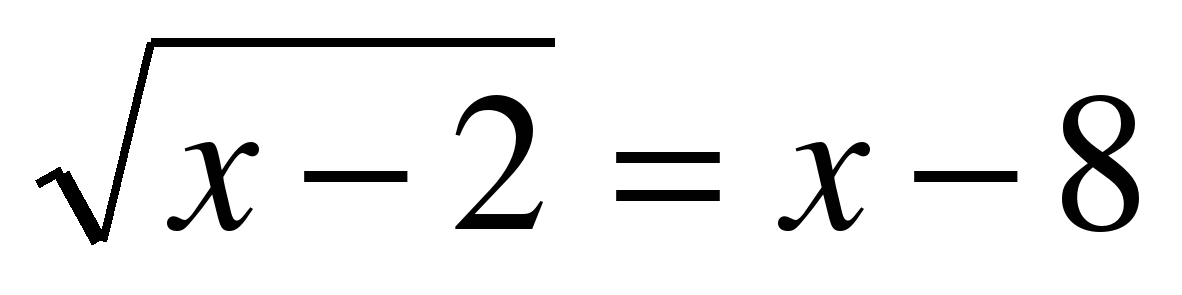
х – 2 = (х – 8)2
х – 2 = х2 - 16х + 64
х2 – 17х + 66 = 0
х1 = 6
х2 = 11
Рассмотрим верное равенство 16 – 36 = 25 – 45.
К обеим частям этого равенства прибавим дробь 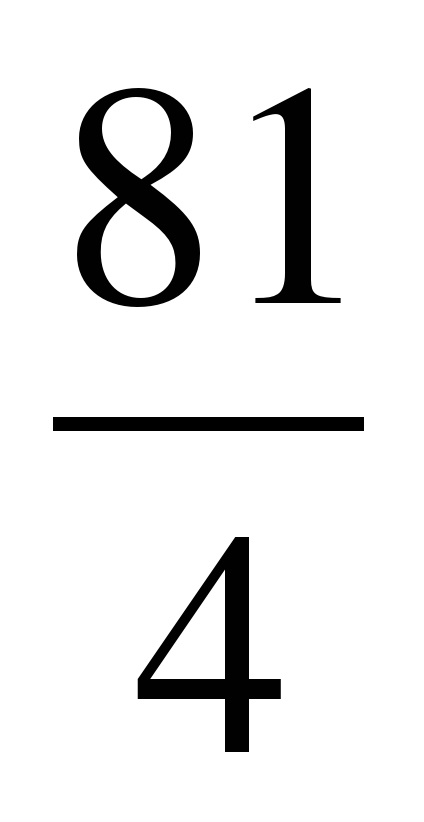

16 – 36 + 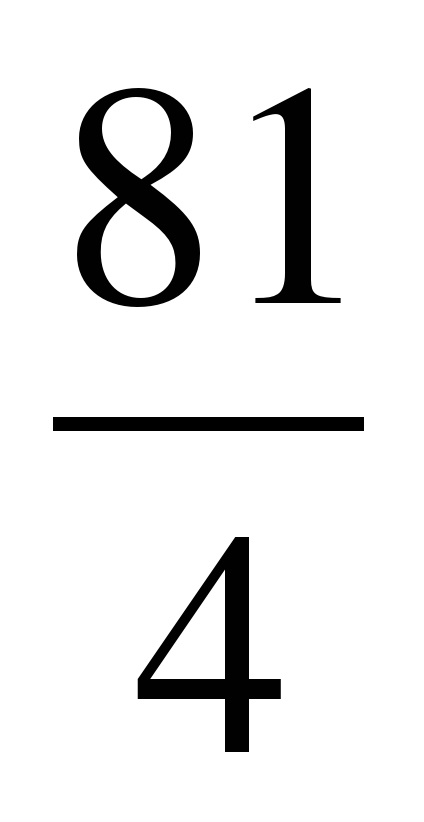 = 25 – 45 +
= 25 – 45 +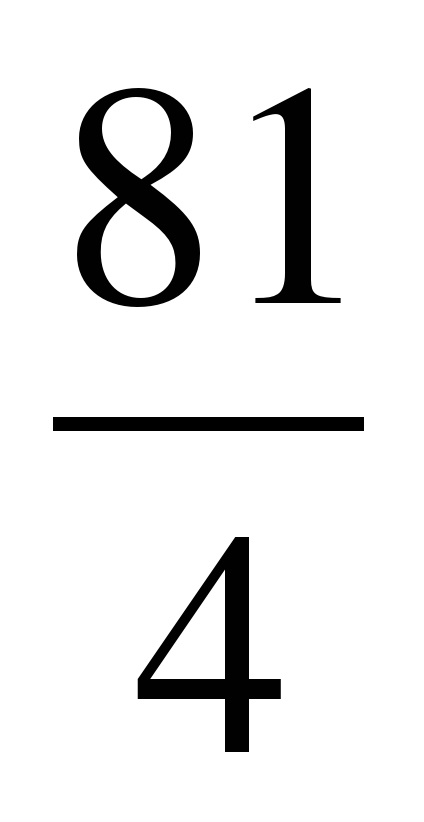 .
.
Выполним преобразования
42 – 2 ∙ 4 ∙ 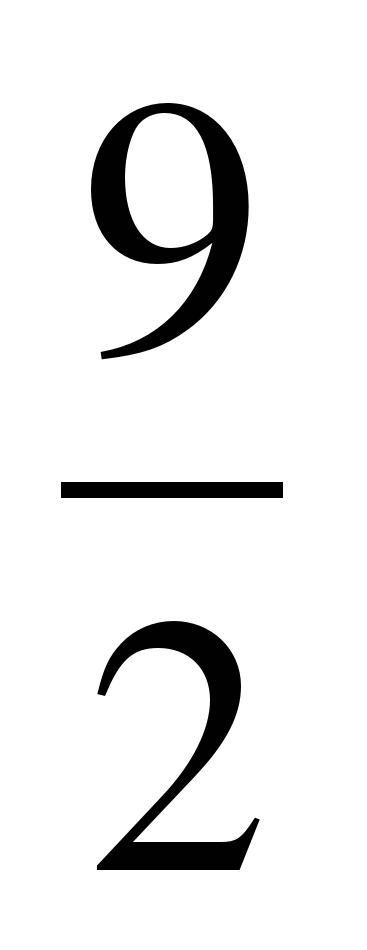 + (
+ (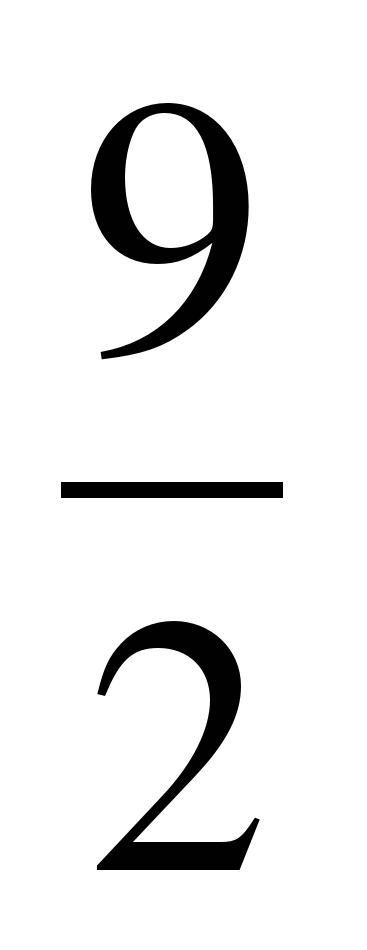 )2 = 52 – 2 ∙ 5 ∙
)2 = 52 – 2 ∙ 5 ∙ 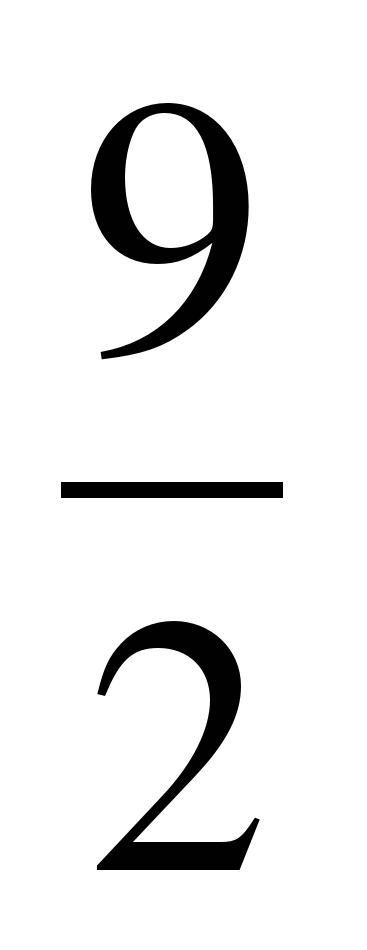 + (
+ (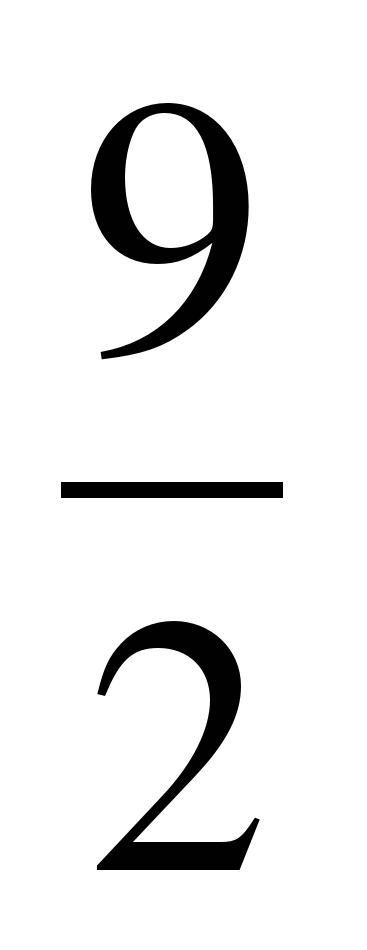 )2
)2
(4 - 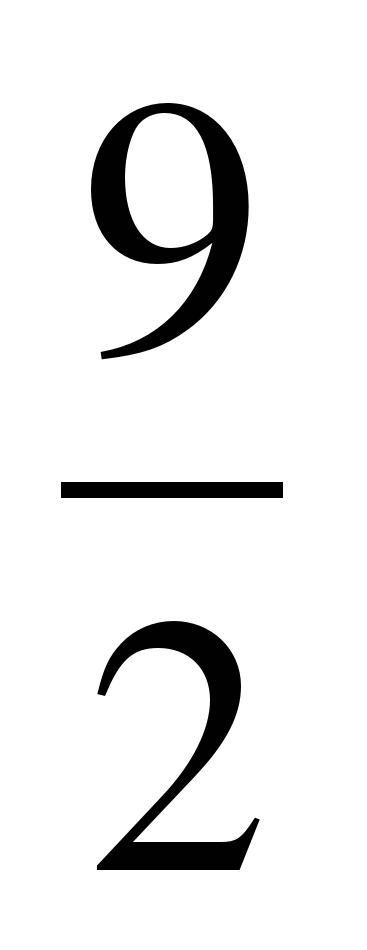 )2 = (5 -
)2 = (5 - 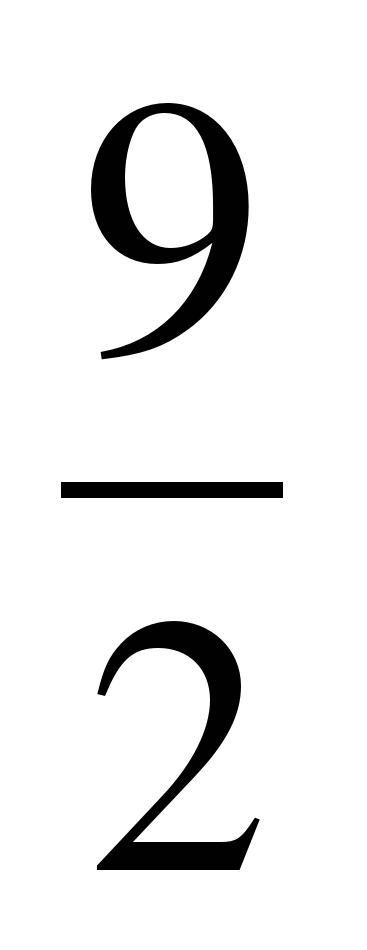 )2
)2
Извлекая из обеих частей равенства квадратный корень, получим
4 - 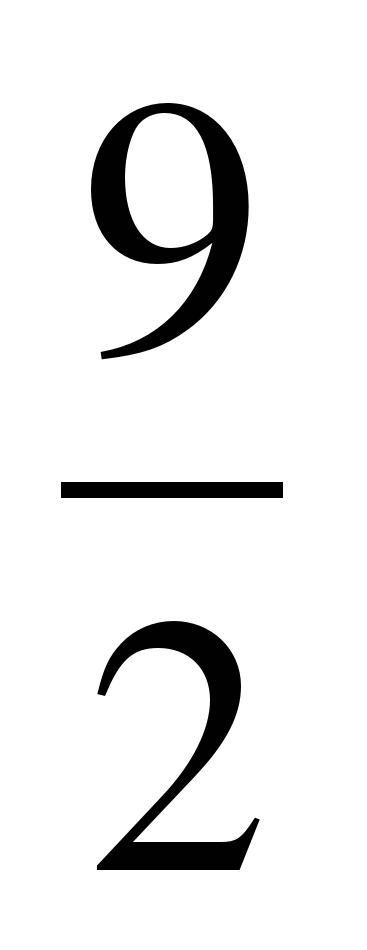 = 5 -
= 5 - 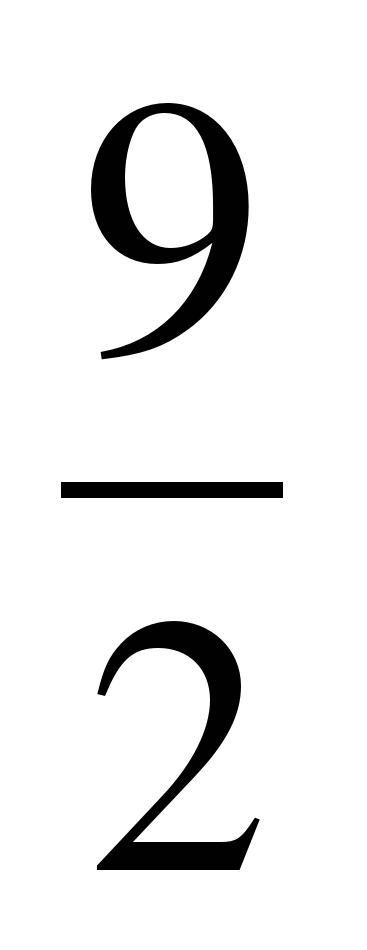 , 4 = 5, т.е. 2 ∙ 2 = 5.
, 4 = 5, т.е. 2 ∙ 2 = 5.
Найдите и объясните ошибку.
А ошибка заключается в том, что из того, что (4 - 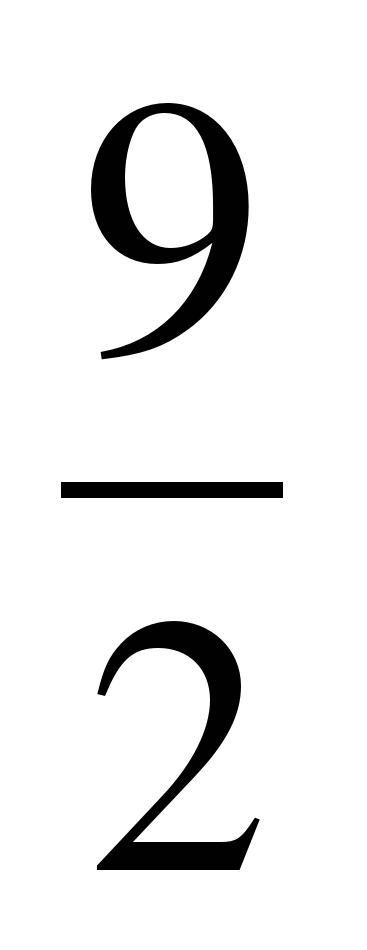 )2 = (5 -
)2 = (5 - 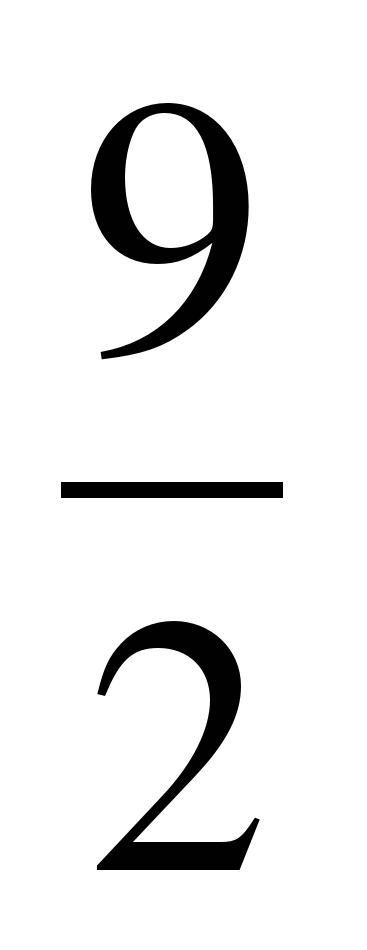 )2 был сделан вывод, что 4 -
)2 был сделан вывод, что 4 - 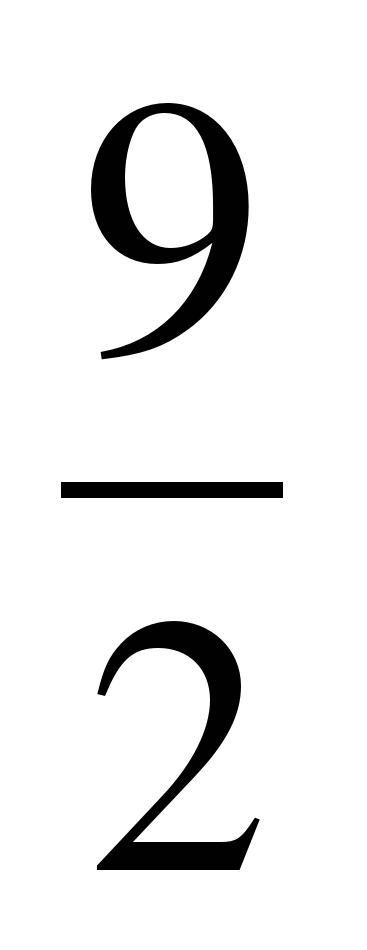 = 5 -
= 5 - 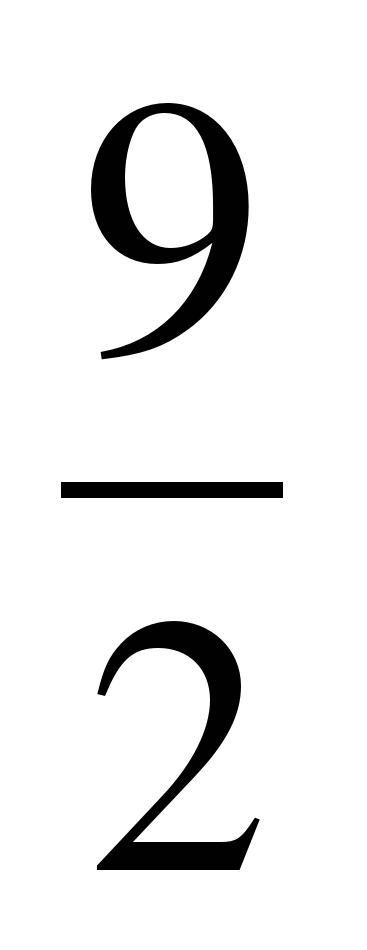 .
.
Этот случай должен предостеречь учащихся от неосмотрительных операций с уравнениями, содержащими переменную под знаком корня.
Вывод 2. При возведении обеих частей уравнения в четную степень возможно появление посторонних корней. Поэтому, при и использовании указанного метода, следует проверить все найденные корни подстановкой в исходное уравнение.
Вернемся к уравнению 2а. Проверка:
если х = 6, то 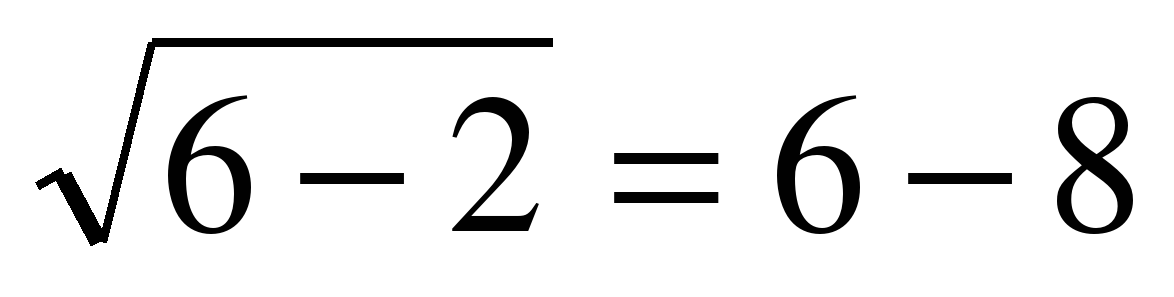 ,
, 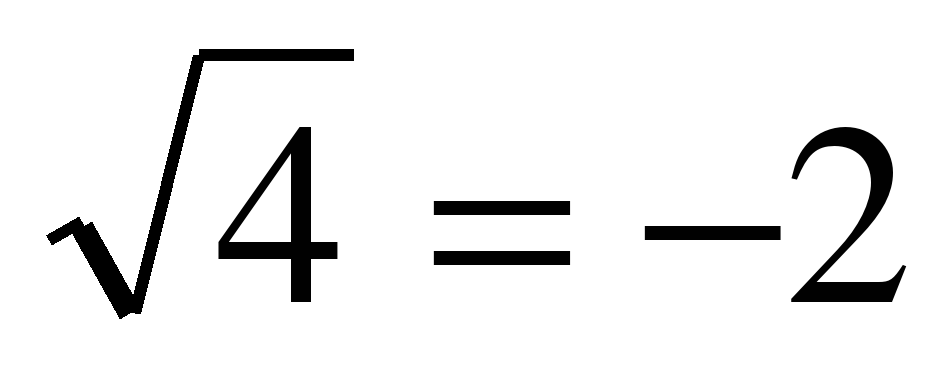 (ложь).
(ложь).
если х = 11, то 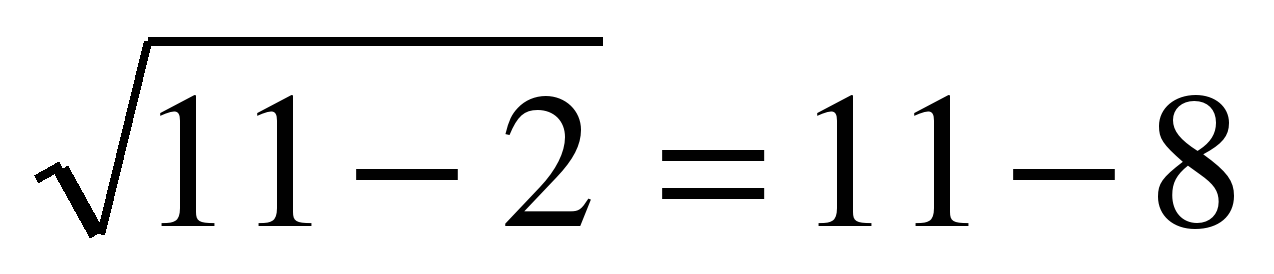 ,
, 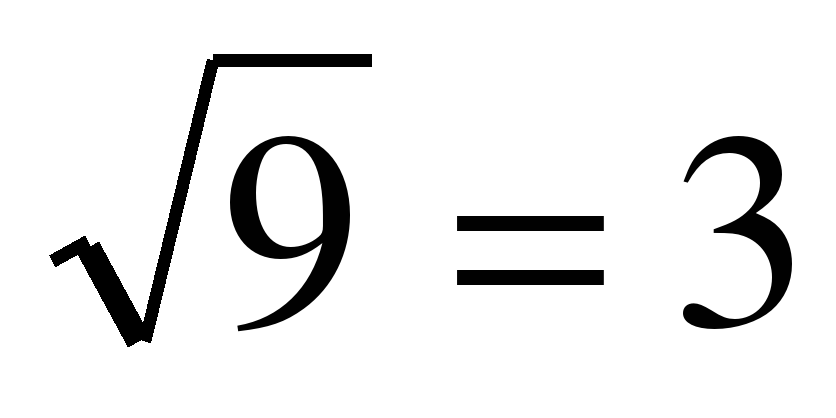 (истина)
(истина)
Ответ: х = 11.
б) ,
в) .
3).Решите уравнения:
а)
Возведя в квадрат обе части данного равенства и решив квадратное уравнение, имеем
х1 =
х2 = -
Проверка: если х = , то

Справедливость этого равенства неочевидна.
Вывод 3.Уравнения вида можно решать, используя определение арифметического квадратного корня:
 В(х) ≥ 0,
В(х) ≥ 0,
А(х) =( В(х))2
Вернемся к уравнению 3а:


 х – 1 ≥ 0 х ≥ 1
х – 1 ≥ 0 х ≥ 1
 7 – 2х – х2 = (х – 1)2 х1 = х1 =
7 – 2х – х2 = (х – 1)2 х1 = х1 =
х2 = -
Ответ: .
б)
в)
4).Решите уравнения:
а) =
 Иррациональные уравнения вида следует решать с помощью равносильного перехода
Иррациональные уравнения вида следует решать с помощью равносильного перехода
А(х) = В(х)
А(х) ≥ 0
Заметим, что в этой системе можно проверять любое из неравенств: А(х) ≥ 0 или В(х) ≥ 0, т.е. следует проверять то, которое в данной задаче проще.
Вернемся к уравнению 4а:

 = х + 2 = 2х – 5 х = 7 х = 7
= х + 2 = 2х – 5 х = 7 х = 7
х + 2 ≥ 0 х ≥ - 2
Ответ: х = 7
б) 
в)
5). Эффективным способом решения иррациональных уравнений является метод введения вспомогательного неизвестного или метод замены переменной. Метод применяется в случае, когда в уравнении неоднократно встречается некоторое выражение, зависящее от неизвестной величины. Тогда имеет смысл это выражение обозначить новой переменной и решить уравнение сначала относительно введенной переменной, а затем уж найти исходную неизвестную.
Решить уравнение:
2х2 + 3х + .
При замене 2х2+3х на а уравнение упрощается, но остается иррациональным. Намного лучше в качестве новой переменной выбрать а = , а ≥ 0, тогда 2х2 + 3х + 9 = а2, 2х2 + 3х = а2 – 9.
По условию а2 – 9 + а = 33
а2 + а – 42 = 0
а1 = - 7
а2 = 6.
а = - 7 не удовлетворяет условию а ≥ 0,
если а = 6, то 2х2 + 3х + 9 = 36
2х2 + 3х - 27 = 0
х1 = -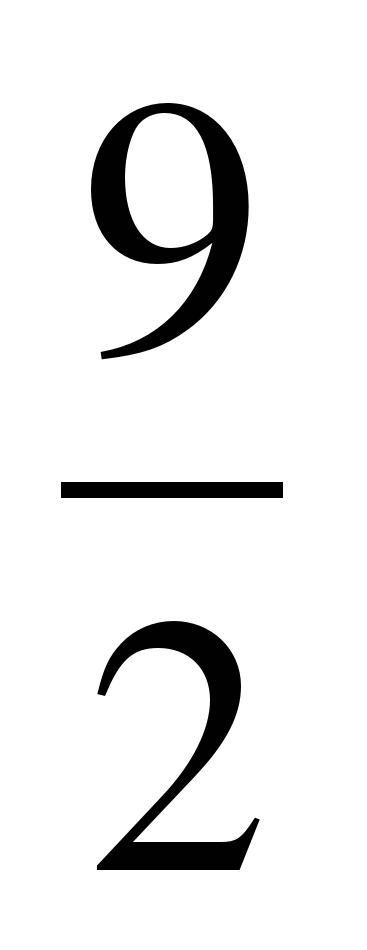
х2 = 3.
Ответ: -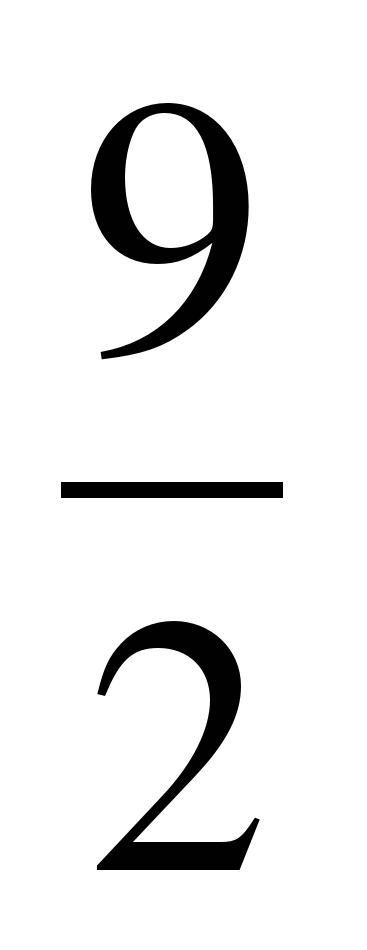 ; 3.
; 3.
6). Если иррациональное уравнение не относится ни к одному из рассмотренных видов, то нужно с помощью различных алгебраических преобразований привести его к одному из этих видов. Обычно для этого используют метод «уединения радикалов» и возведение в степень.
а)
б)
в)


 Получите свидетельство
Получите свидетельство Вход
Вход












 Методическая разработка факультативного занятия по математике "Способы решения иррациональных уравнений" (0.13 MB)
Методическая разработка факультативного занятия по математике "Способы решения иррациональных уравнений" (0.13 MB)
 0
0 808
808 133
133 Нравится
0
Нравится
0


