Определение: Системой уравнений называются несколько уравнений от одной или нескольких переменных, которые должны выполняться одновременно, т.е. при одинаковых значениях переменных для всех уравнений. Уравнения в системе объединяются знаком системы – фигурной скобкой.
Пример 1:
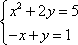
- система двух уравнений с двумя переменными x и y.
Решением системы являются корни 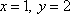 . При подстановке этих значений уравнения превращаются в верные тождества:
. При подстановке этих значений уравнения превращаются в верные тождества:
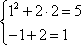
Решение систем линейных уравнений.
Самым распространенным методом решения системы является метод подстановки.
Метод подстановки.
Метод подстановки для решения систем уравнений заключается в том, чтобы из одного уравнения системы выразить какую-либо переменную через другие, и подставить это выражение в остальные уравнения системы вместо выраженной переменной.
Пример 2:
Решить систему уравнений:
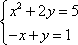
Решение:
Дана система уравнений и ее требуется решить методом подстановки.
Выразим переменную y из второго уравнения системы.
Замечание: «Выразить переменную» означает преобразовать равенство так, чтобы эта переменная осталась слева от знака равенства с коэффициентом 1, а все остальные слагаемые перешли в правую часть равенства.
Второе уравнение системы:
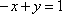
Оставим слева только y:
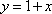
И подставим (вот оттуда то и идет название метода) в первое уравнение вместо у выражение, которому оно равно, т.е.  .
.
Первое уравнение :
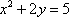
Подставим 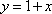 :
:
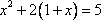
Решим это банальное квадратное уравнение. Для тех, кто забыл, как это делается, есть статья Решение квадратных уравнений..
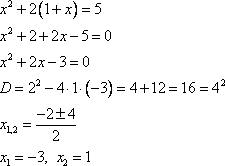
Итак, значения переменной x найдены.
Подставим эти значения в выражение для переменной y. Здесь получилось два значения x, т.е. для каждого из них следует находить значение y .
1) Пусть 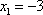
Подставляем в выражение 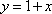 .
.
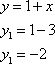
2) Пусть 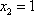
Подставляем в выражение 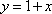 .
.
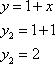
Все можно составлять ответ: 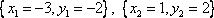
Замечание: Ответ в этом случае следует записывать попарно, чтоб не перепутать, какое значение переменной y соответствует какому значению переменной x.
Ответ: 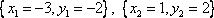
Замечание: В примере 1 как решение системы указана только одна пара, т.е. эта пара является решением системы, но не полным. Потому, как решить уравнение или систему значит указать решение и показать, что других решений нет. А тут еще одна пара.
Оформим решение этой системы по-школьному:
Замечание: Знак « » значит «равносильно», т.е. следующая система или выражение равносильно предыдущей.
» значит «равносильно», т.е. следующая система или выражение равносильно предыдущей.
Пример 3:
Решить систему уравнений:
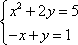
Решение:
Дана система уравнений и ее требуется решить методом подстановки.
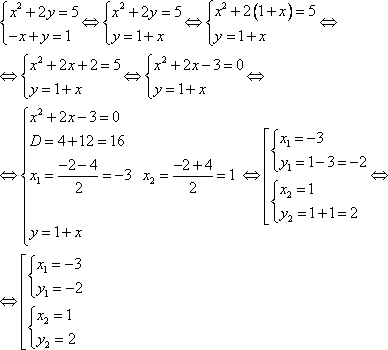
Ответ: 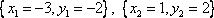
Замечание: Отличие от примера 1 заключается в том, что система всегда пишется полностью, т.е. даже то уравнение, которое не преобразуется. Это лишний труд.
Замечание: Очень-очень часть ответ, записанный здесь в виде
школьные учителя записывают в виде 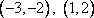 , делая заявление, что переменные перечислены по алфавиту. Но это делать глупо, решающий человек должен максимально исключить двусмысленность своей записи, а запись
, делая заявление, что переменные перечислены по алфавиту. Но это делать глупо, решающий человек должен максимально исключить двусмысленность своей записи, а запись 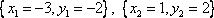 не оставляет место для вопросов.
не оставляет место для вопросов.


 Получите свидетельство
Получите свидетельство Вход
Вход


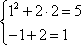
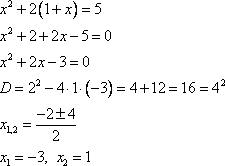
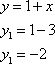
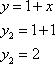
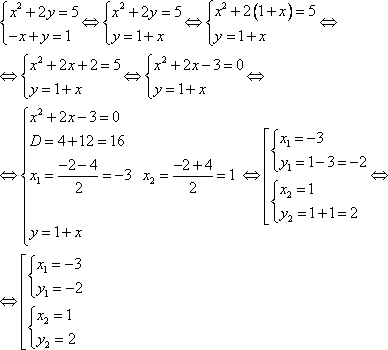









 Метод подстановки (методическая разработка) (26.79 КB)
Метод подстановки (методическая разработка) (26.79 КB)
 0
0 889
889 51
51 Нравится
0
Нравится
0


