"Математика и эстетика"

Математика и эстетика

Левшиц Р.Я., учитель математики,

ГУО «Лунинская ясли –сад- средняя школа»

1. Введение

Одной из важнейших целей проведения внеклассной работы по математике является развитие интереса учащихся к математике. У учащихся имеется большое желание проверить свои силы, математические способности, умение решать нестандартные задачи. Их привлекает возможность добровольного участия.

Поэтому необходимо использовать все возможности внеклассной работы по математике и с её помощью осуществлять подготовку учащихся к более глубокому изучению предмета. Надо создать детям такие условия, чтобы им захотелось в дальнейшем изучать математику на повышенном уровне.

2.Основная часть

Математика и эстетика

Исходя из своего опыта работы, я обратила внимание на то, что учащимся нравится решать задачи, у которых есть или занимательный сюжет, или нестандартный подход в решении. Поэтому в своей работе при проведении внеклассных мероприятий я стараюсь подобрать учащимся задачи такого типа, чтобы подогревать интерес к изучению предмета.

Сначала немного теории.

Цель моей работы:

Пропагандировать красоту математики, способствовать развитию интереса к изучению математики.

Задачи:

• рассмотреть формулу математической красоты.

• разобрать ряд задач, имеющих изящный подход в решении, подтверждающий формулу математической красоты.

Итак, я показываю учащимся, на примере решения задач, как связать вместе казалось бы абсолютно несовместимые вещи - математику и эстетику. Красота с точки зрения математики-понятие относительное, кто-то её видит, а кто-то нет.

Ещё Рене Декарт писал: «К области математики относят науки, в которых рассматриваются либо порядок, либо мера, и совершенно несущественно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое…; таким образом, должна существовать некая общая наука, объясняющая всё».

Эстетика-красота, художественность в оформлении, организации чего-нибудь (С.И.Ожегов «Словарь русского языка»).

Однако, интерес к математике удел немногих. В чём же состоит красота математики? Как связать математику и эстетику, чтобы учащимся нравилось заниматься такой сложной наукой?

Почему одно решение задачи оставляет нас лишь спокойно удовлетворёнными, тогда как другое решение вызывает эмоциональный подъём, поражает смелостью замысла и изяществом?

Понятие наглядности. Его основные черты.

Для того чтобы понять, что еще, помимо необычности должно характеризовать математическое рассуждение, обратимся к понятию наглядности.

Две основные черты наглядности - изоморфизм и простота. Если мы хотим понять некоторое явление, яснее представить его составные части, их взаимосвязь, то мы прибегаем к наглядной модели изучаемого явления. Наглядная модель должна правильно отражать те основные черты явления, которые подлежат изучению. В самом деле, если бы они были представлены искаженно, то нельзя было бы говорить о модели изучаемого явления.

Математически правильное, неискаженное отражение основных свойств явления описывается понятием изоморфизма.

Чтобы быть наглядной, модель должна быть простой для восприятия, для оперирования с нею. При применении наглядности мы как бы осуществляем перевод с языка сложного явления на более простой язык наглядной модели.

Схема применения наглядности

Вместо того, чтобы напрямик пробираться через непроходимые «джунгли явления», мы переплываем реку на «берег наглядной модели» и там по благоустроенному шоссе движемся к «городу необходимых выводов», а достигнув его, снова переплываем реку и приходим к заветной цели.

Чем дальше от тематики задачи отстоит использованная теорема, тем более удивительной кажется вначале мысль о ее применении, тем больше ощущение красоты найденного решения. А если для получения наглядной модели задачи нужно применить неожиданную комбинацию из нескольких теорий, методов рассуждения, то такое решение производит впечатление искусства.

Формула математической эстетики

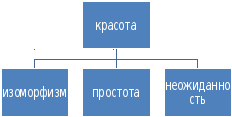
Эта формула, несомненно, связана с математической культурой. Задачи, решение которых заставляет думать, сопоставлять различные методы, искать иные формулировки воспитывают хороший вкус и математическую культуру

В рамках недели математики, декады математики, на факультативных занятиях имеет смысл предоставлять учащимся ряд задач, решение которых, с точки зрения учителя ,может вызвать удивление, положительные эмоции, оказывается нестандартным и красивым.

Например, самая простая задача о 9 точках.

Рассматривая 9 точек, расположенных в вершинах квадрата, его центре и серединах сторон, требуется построить четырехзвенную ломанную, проходящую через все эти 9 точек.

Решение.

На рисунке изображены, конечно, не точки, но их расположение соответствует условию задачи, т.е. дает изоморфную модель изучаемого явления. Вместе с тем, эта модель, несомненно, проста для восприятия, т.е. является наглядной моделью.

Решить задачу, как правило, не удается. Решающий вычеркивает ломанные, но все они состоят из пяти звеньев. После ряда неудачных попыток одни говорят «не знаю», другие «невозможно». И когда им показывают решение, они находят его красивым.

Поскольку наглядность налицо, изящество решения - в его неожиданности: ломанная пересекает себя и выходит за пределы квадрата. Выход за пределы квадрата казался невозможным, совершенно лишним, бессмысленным, а между тем именно здесь и было скрыто решение.

Или задача о попе и его работнике Балде.

Поп и Балда играют в следующую игру: каждый кладёт пятак на стол по очереди. Тот , кто положит на стол последний пятак так, чтобы поверхность стола вся была закрыта пятаками выигрывает. Какой тактики надо придерживаться, чтобы выиграть?

Решение.

Для решения этой задачи необходимо воспользоваться понятием центральной симметрии. Первый пятак – в центр стола, второй - где угодно. Третий - симметрично второму, четвертый – где угодно, пятый – симметрично четвертому и т.д. выиграет тот, кто догадается первым положить пятак в центр стола.

Решение задачи становится очевидным, если изобразить соответствующий рисунок. Я считаю, что принцип простоты и неожиданности в решении этой задачи соблюдён.

Я предлагаю к условию задач выполнять простые рисунки (см. Приложение ), это внесёт элемент красоты и может привлечь учащихся.

3.Заключение

Внеурочная работа по математике предоставляет учащимся дополнительные возможности для развития способностей, прививает интерес к математике, способствует осуществлению допрофильной подготовки по предмету. Главное назначение внеклассной работы – не только расширение и углубление теоретического материала, изученного на уроках, но и способствовать развитию умений применять полученные на уроках знания к решению нестандартных задач. Учитель, занимающийся внеклассной работой с учащимися, не стоит на месте, а постоянно занимается самообразованием, повыщает свой профессиональный и интеллектуальный уровень.

Литература

1. Болтянский В.Г. Математическая культура и эстетика. Математика в школе, 1982 №1 с.16-18

2. Герман Ш.М., Скатерщиков В.К. Беседы об эстетике.-М: Знание, 1982.-224с.

3. Зенкевич И.Г. Эстетика урока математики: Пособие для учителей. –М.: Просвещение, 1981

4. Мазаник А.А. Реши сам.-2-е изд., перераб.-Мн. :нар.асвета,1980.-239с.,ил.

5. Мерзляк А.Г., Полонский В.Б., Якир М.С. Неожиданный шаг или сто тринадцать красивых задач.- Киев.: Агрофирма «Александрия», 1993

ПРИЛОЖЕНИЕ

Задача о точках

Как шестью линиями соединить 16 точек, не отрывая карандаш от бумаги и не проводя по одной линии дважды.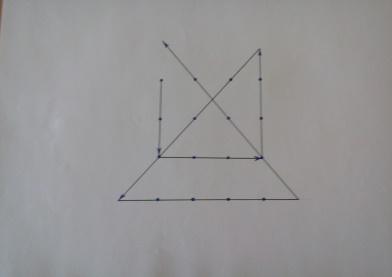

Задача о пароходах

На одном научном конгрессе математиков во время завтрака присутствующим была предложена следующая задача. Представьте себе, что каждый день в полдень из Гавра (Франция) в Нью-Йорк (США) отправляется почтовый пароход и в то же время из Нью-Йорка отходит идущий в Гавр пароход той же компании. Каждый из этих пароходов находится в пути ровно 7 суток. И идут они по одному и тому же пути. Сколько пароходов своей компании встретит на своём пути пароход, идущий из Гавра в Нью-Йорк?

Задача о кузнечиках

В трёх вершинах квадрата сидят кузнечики и играют в чехарду. Это происходит следующим образом: кузнечик прыгает по прямой через другого кузнечика и приземляется на таком же расстоянии от него, ка и был с другой стороны. Сможет ли какой – нибудь кузнечик попасть в четвёртую вершину квадрата?

Задача о жуках

В каждой клетке доски 5 на 5 сидит жук. В некоторый момент все жуки переползают на соседние клетки (по горизонтали или вертикали) клетки. Обязательно ли при этом останется пустая клетка?

Задача о мышке

Мышка грызёт куб сыра с ребром 3, разбитый на 27 единичных кубиков. Когда мышка съедает какой-либо кубик, она переходит к другому, имеющему с предыдущим общую грань. Может ли мышка съесть весь куб, кроме среднего кубика?

Шестиугольник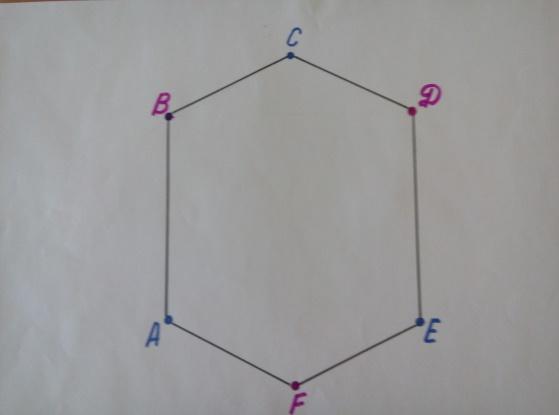

В вершинах шестиугольника ABCDEF записаны числа 2,7,9,10,3,12 соответственно указанному порядку букв. За один шаг к двум соседним вершинам можно прибавить или вычесть одно и то же число. Можно ли за несколько шагов из указанной шестерки чисел получить следующую: 5,11.6,15,8,14. Сохранив порядок соответствия чисел вершинам?

Геометрия помогает алгебре

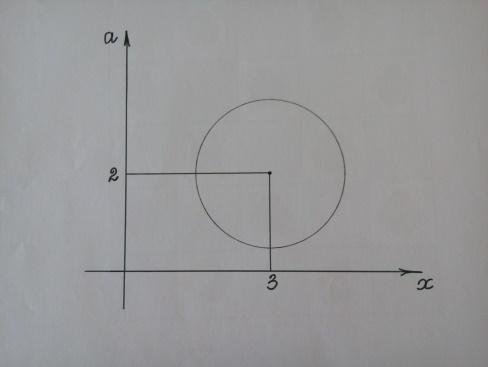
При каком значении параметра а модуль разности корней уравнения х² -6х +12+а² -4а=0 принимает наибольшее значение?

Детские работы

.