
Деление многочленов
Перминова Е.В.
ГАПОУ СО «СОПК»

09/22/2021
Цели
- Повторить понятие одночлена, многочлена;
- Повторить действия с одночленами и многочленами;
- Ознакомить с алгоритмом деления многочлена на многочлен.

09/22/2021
Повторение
- Одночлен
- Стандартный вид одночлена
- Степень одночлена
- Действия с одночленами
- Многочлен
- Степень многочлена
- Старший член многочлена
- Действия с многочленами

09/22/2021
Одночлен
Одночленом называют
алгебраическое выражение, которое представляет собой произведение чисел и переменных, возведенных в степень с натуральными показателями:
; ; ;

09/22/2021
Стандартный вид одночлена: −5𝑎𝑐3𝑎^𝟓
- Чтобы привести одночлен к стандартному виду, нужно:
- 1. Перемножить все числовые множители и поставить их на первое место;
- 2. Перемножить все имеющие степени с одним буквенным основанием;
- 3. Перемножить все имеющие степени с другим буквенным основанием и т.д.
- Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена

09/22/2021
Степенью одночлена называют сумму показателей степеней всех входящих в него переменных. Если одночлен не содержит переменных и является числом, отличным от нуля, то степень этого одночлена считают равной нулю.
Например:
Сумма показателей степени всех переменных равна 6
Значит это одночлен 6 степени

09/22/2021
Действия с одночленами
- Умножение одночленов
- Возведение одночленов в степень
- Деление одночленов
- Сложение и вычитание
Выполни действия

09/22/2021
Многочлен
Многочленом называется сумма одночленов
– двучлен
– трехчлен
Одночлен считают многочленом, состоящим из одного члена

Многочлены 5 х² − 6 х − 2 ; − 4 х³ + 2 х² − 3 х
записаны в стандартном виде, и показатели
степеней буквы х расположены в порядке
убывания.
Тогда первый член многочлена − это его
старший член;
показатель степени буквы х в старшем члене −
это степень многочлена;
член многочлена, не содержащий буквы х − это
свободный член.
5 х² − 6 х − 2 − это многочлен второй степени;
− 4 х³ + 2 х² − 3 х − это многочлен третьей степени.

Повторение
Выполнить деление:
4)
1)
2)
5)
6)
3)
Выполнить вычитание:
3)
2)
1)
─
─
─

Деление многочленов на цело
При сложении, вычитании, умножении многочленов
получается многочлен, например:
1. (5х²+3х+6)+( − 3х²+4х−9)= 5х²+3х+6 − 3х²+4х−9 = 2х²+7х − 3;
2. ( − 2х²+7х) −( 3х²+х+1)= − 2х²+7х − 3х² − х−1 = − 5х² + 6х − 1 ;
3. (х+5)(х² − 3) = х³ − 3х + 5х² − 15.
При делении многочлена на многочлен может получиться
многочлен, тогда деление выполнено нацело.

делимое
делимое
делимое
Разделить многочлен 3х³ − 5х² − 6х + 8 на многочлен
3х² + х − 4.
Деление можно выполнить уголком, как и деление
натуральных чисел:
делитель
3х² + х − 4
3х³ − 5х² − 6х + 8
делимое
делимое
─
− 2
частное
х
3х³ + х² − 4х
− 6х² − 2х
первый остаток
делимое
+ 8
─
− 6х² − 2х + 8
остаток
0
Остаток равен нулю, поэтому многочлен 3х³ − 5х² − 6х + 8
делится нацело на многочлен 3х² + х − 4, т. е. в
результате деления многочленов снова получился
многочлен.

Алгоритм деления многочленов уголком
1. Расположить делимое и делитель по убывающим
степеням переменной х .
2. Разделить старший член делимого на старший член
делителя;
полученный одночлен записать первым членом частного.
3. Первый член частного умножить на делитель,
результат вычесть из делимого;
полученная разность является первым остатком.
4. Старший член этого остатка разделить на старший
член делителя; полученный одночлен записать вторым
членом частного и умножить его на делитель;
результат вычесть из первого остатка; получим
второй остаток и т. д.
Это следует продолжить до тех пор, пока не будет
получен остаток, равный нулю.

Как и при делении чисел, результат деления
многочленов можно проверить умножением.
Если многочлен
степени n ≥ 1 делится нацело на
степени k ≥ 1, k ≤ n и в результате
многочлен
получается многочлен
степени m ≥ 1, m ≤ n, то
справедливо равенство
Это равенство называют формулой деления многочлена
а многочлен
на многочлен
называют частным от деления
на
при этом обязательно, чтобы n = m + k.

Свойства делимости многочленов
1. Если многочлен P( x ) делится на многочлен Q( x ), а многочлен Q( x ) делится на многочлен M( x ) , то многочлен P( x ) делиться на многочлен M( x ) .
2. Если многочлены P( x ) и Q( x ) делятся на многочлен M( x ), то многочлены P( x ) + Q( x ) и P( x ) Q( x ) делятся на многочлен M( x ), а многочлен P( x ) Q( x ) делиться на многочлен M 2 ( x ) .

Найти частное (результат проверить умножением):
2) ( − 4х² − х + 5) : (4х + 5);
1) (х² − 2х − 35) : (х − 7);
4х + 5
х − 7
− 4х² − х + 5
х² − 2х − 35
─
─
+ 1
− х
х² − 7х
− 4х² − 5х
х
+ 5
− 35
5х
+ 5
4х
─
─
5х − 35
4х + 5
0
0
(х + 5) (х − 7) = х² − 7х + 5х − 35 = х² − 2х − 35;
(4х + 5) ( − х + 1) = − 4х² − 5х + 4х + 5 = − 4х² − х + 5.

№ 1. Найти частное (результат проверить умножением):
3х − 1
6х³ + 7х² − 6х + 1
─
6х³ − 2х²
+ 3х
2х²
− 1
9х²
− 6х
─
9х² − 3х
− 3х
+ 1
─
− 3х + 1
0
(2х² + 3х − 1) (3х − 1) =
6х³ − 2х² + 9х² − 3х − 3х + 1 =
= 6х³ + 7х² − 6х + 1
показать

№ 2. Найти частное (результат проверить умножением):
2х² + 3х − 1
6х³ + 11х² − 1
─
3х
+ 1
6х³ + 9х² − 3х
− 1
2х² + 3х
─
2х² + 3х − 1
0
(3х + 1)(2х² + 3х − 1) =
6х³ + 9х² − 3х + 2х² + 3х − 1 =
= 6х³ + 11х² − 1
показать
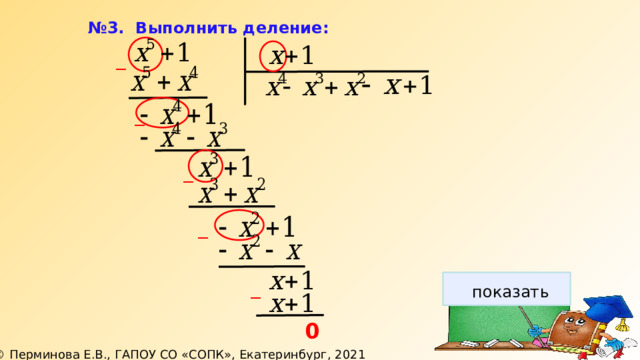
№ 3. Выполнить деление:
─
─
─
─
показать
─
0

№ 4. Выяснить, делится ли нацело многочлен Р(х)
на многочлен Q(x):
─
2х³
+ 3х²
─
0
Ответ: делится, т. к остаток равен нулю.
показать

№ 5. Выяснить, при каком значении а многочлен Р(х) делится нацело на многочлен Q(x):
Р(х) = 5х³ − 9х² + 13х + а,
Q(х) = 5х + 1
Выполним деление уголком:
5х + 1
5х³ − 9х² + 13х + а
─
х²
+ 3
− 2х
5х³ + х²
− 10х²+13х
─
− 10х² − 2х
15х + а
─
По смыслу задания
остаток а − 3 должен
равняться нулю,
поэтому а − 3 = 0, а = 3.
15х + 3
а − 3
Ответ: при а = 3.

Q(х) = х² − 3х + 1
Р(х) = 7х³ − 22х² + а х − 1,
№ 6
х² − 3х + 1
7х³ − 22х² + а х − 1
─
− 1
7х³ − 21х² + 7х
7х
− 7х² − 7х+ а х − 1
─
− 7х² + 3х − 1
ах − 10х
По смыслу задания надо найти те значения а,
при которых остаток ах − 10х = (а − 10)х должен
равняться нулю, поэтому а − 10 = 0, а = 10.
Ответ: при а = 10.

№ 7. Найти такой многочлен Q(х), чтобы многочлен Р(х)
делился нацело на Q(х) и частное от деления
равнялось М(х).
1) Р(х ) = 4х³ − 5х² + 6х + 9,
М(х) = х² − 2х + 3.
Решение. По формуле деления должно выполняться
равенство Р(х) = М(х) ∙ Q(х). Задача свелась к
нахождению делителя по известным делимому и
частному. Поэтому Q(х) = Р(х) : М(х)
х² − 2х + 3
4х³ − 5х² + 6х + 9
─
4х³ − 8х² + 12х
4х
+ 3
3х² − 6х + 9
─
3х² − 6х + 9
0
Ответ: Q(х) = 4х + 3.

Деление многочленов с остатком
Покажем деление многочленов в случаях, когда
многочлены не делятся нацело.
Разделить многочлен х³ − х² − 2х + 4 на многочлен
х² − 3х + 1.
Выполним деление уголком:
х² − 3х + 1
х³ − х² − 2х + 4
─
х
+ 2
х³ − 3х² + х
Дальнейшее деление
невозможно, так как степень
последнего остатка 1
меньше степени делителя 2.
+ 4
2х² − 3х
─
2х² − 6х + 2
3х + 2
Ответ: частное х + 2, остаток 3х + 2.

Деление многочленов с остатком
Формула деления многочлена
степени n ≥ 1 на
многочлен
степени k ≥ 1, k ≤ n с остатком
такова:
При этом степень частного m = n − k,
степень остатка l
называют неполным частным,
Многочлен
многочлен
называют остатком.

№ 1. Написать формулу деления многочлена Р(х) на
многочлен Q(х):
3) Р(х ) = 6х³ + 3х² − 4х + 3,
Q(х) = 2х + 1
Решение. Формула деления:
Выполним деление Р(х) на Q(х) с остатком:
2х + 1
6х³ + 3х² − 4х + 3
─
3х²
─ 2
6х³ + 3х²
− 4х + 3
─
− 4х ─ 2
5
Р(х ) = (3х² − 2) ∙ Q(х) + 5,
показать

№ 2. Найти частное М(х) и остаток R(x) от деления
многочлена Р(х) на многочлен Q(х):
Q(х) = 2х² + 5
2) Р(х ) = х³ − 3х²,
Решение. Выполним деление Р(х) на Q(х) с остатком R(x) :
2х² + 5
х³ − 3х²
─
─ 1,5
0,5х
х³ + 2,5х
− 3х² − 2,5х
─
− 3х² ─ 7,5
− 2,5х + 7,5
Ответ: частное М(х ) = (3х² − 2);
остаток R(х) = − 2,5х + 7,5.
показать

№ 3 Найти такой многочлен Q(х), чтобы при делении
многочлена Р(х) на Q(х) частное было равно М(х)
и остаток был равен R(x).
Р(х ) = 2х³ − 3х + 5,
М(х) = 2х − 4,
R(х) = 5х + 5.
Решение. По формуле деления должно выполняться
равенство Р(х) = М(х) ∙ Q(х) + R(x). Задача свелась к
нахождению делителя по известным делимому, частному
и остатку. Поэтому 2х³ − 3х + 5 =(2х − 4)∙ Q(х) + 5х + 5,
(2х − 4)∙ Q(х) = 2х³ − 3х − 5х, откуда
Q(х) = (2х³ − 8х) : (2х − 4).

2х − 4
Выполним деление:
2х³ − 8х
─
х²
2х³ − 4х²
+ 2х
4х² − 8х
─
4х² − 8х
0
Ответ: Q(х) = х² + 2х.

27
09/22/2021
Домашнее задание
- Найти частное (результат проверить умножением)

09/22/2021
27
Домашнее задание
Найдите частное
- ( x 2 +3 х 4):( х + 4)
- ( x 2 7 х + 10):( х 5)
- (6 x 3 +7 х 2 6 х + 1):(3 х 1)
- (4 x 3 5 х 2 + 6 х + 9):(4 х + 3)
- (15 x 3 х 2 + 8 х 4):(3 х 2 + х + 2)
- (9 х 4 9 x 3 х 2 + 3 х 2):(3 х 2 2х + 1)

 Получите свидетельство
Получите свидетельство Вход
Вход












 Математика 1 курс СПО. "Деление многочленов" (967.94 KB)
Математика 1 курс СПО. "Деление многочленов" (967.94 KB)
 0
0 418
418 10
10 Нравится
0
Нравится
0


