Математика 1 курс СПО. "действительные числа"

ПОНЯТИЕ О РАЗВИТИЕ ЧИСЛА

ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.

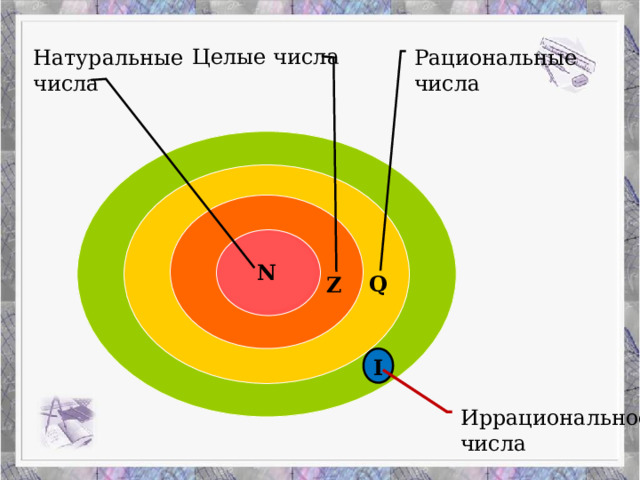
Целые числа

Рациональные

Натуральные

числа

числа

N

Q

Z

I

Иррациональное

числа

Числа, которые не являются рациональными, то есть не являются ни целыми, ни представимыми в виде дроби вида  , где m – целое число, а n – натуральное, называются   иррациональными .

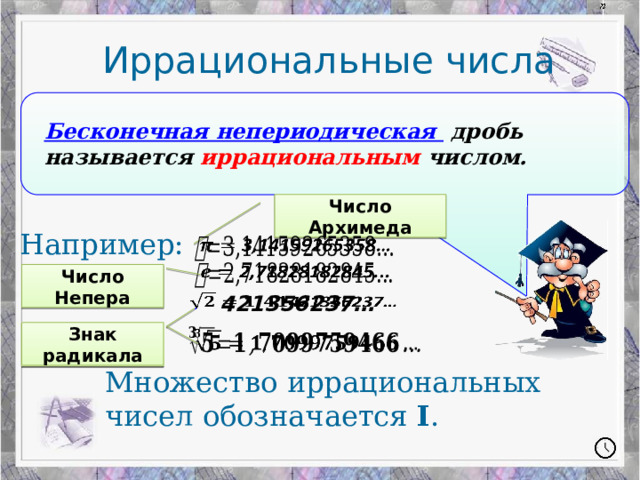
Иррациональные числа

Бесконечная непериодическая дробь называется иррациональным числом.

Число Архимеда

Например:

Число Непера

421356237…

Знак радикала

Знак радикала

Множество иррациональных чисел обозначается I .

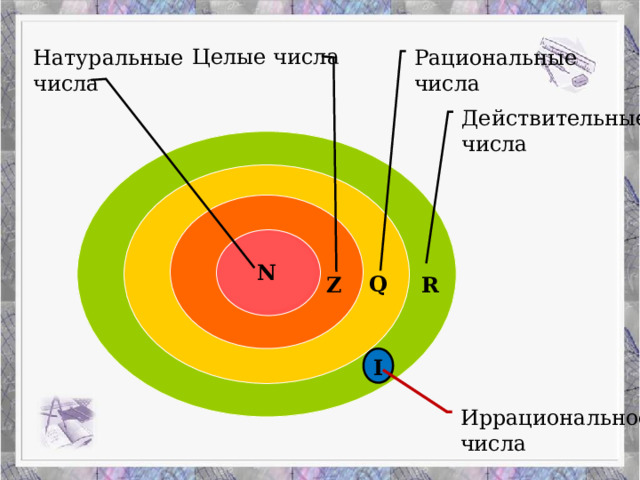
Целые числа

Натуральные

Рациональные

числа

числа

Действительные

числа

N

Q

Z

R

I

Иррациональное

числа

Действительные числа

• R=(рациональные числа, иррациональные числа)
• Действительные числа не обладают свойством замкнутости - не всякое уравнение имеет корни.

Извлечение квадратного корня из числа

I

II

1. Сгруппировать по 2 цифры числа, с права на лево

8

1

2. Из II группы цифр вычесть 1

7

3. Далее вычитать следующее нечетное натуральное число

3

4

4. Посчитать сколько вычитаний было сделано

5. И получившееся число записать после знака равенства

Извлечение квадратного корня из числа

I

II

53

4

6. К получившемуся числу добавить цифры I группы

41

51

412

177

7. Далее применим вычисления с последним вычитаемым

53

43

124

369

55

45

Получим нечетное натуральное число, которое и будет нашим следующим вычитаемым

69

324

57

47

12

8. Далее выполняем действия пп. 3-5

277

49

228

228

Извлечение квадратного корня из числа

12

00

9. К получившемуся числу добавить два нуля

581

619

10. В результате поставить запятую

583

11. Далее применим вычисления с последним вычитаемым

36

Получим нечетное натуральное число, которое и будет нашим следующим вычитаемым

12. Далее выполняем действия пп. 3-5

Извлечение квадратного корня из числа

0

00

00

36

…

58401

13. Выполнить пп. 9,11

301599

14. Получившееся число 5841

58403

15. К получившемуся числу добавить еще два нуля

243196

58405

16. Далее применим вычисления с последним вычитаемым

184791

58407

126284

Получим нечетное натуральное число, которое и будет нашим следующим вычитаемым

58409

67875

58411

17. В результате добавим нуль

9464

18. Далее выполняем действия пп. 3-5

Извлечение квадратного корня из числа

0

…

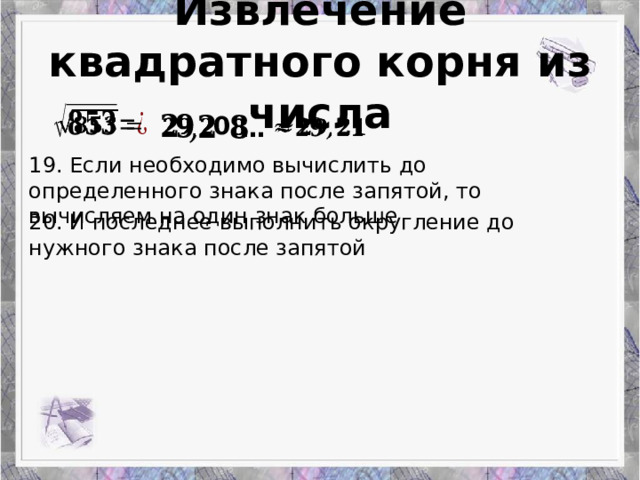
19. Если необходимо вычислить до определенного знака после запятой, то вычисляем на один знак больше

20. И последнее выполнить округление до нужного знака после запятой

Вычислить

Домашнее задание

• до десятых
• до сотых
• до тысячных
• до сотых
• до тысячных
• до десятых

• до сотых
• до десятых
• до тысячных
• до сотых