Математические модели

^{Практическая работа}

«Математические модели в профессиональной области»

Цель работы: закрепление практических навыков в построении математических моделей при решении химических задач.

Теоретический материал

Модель – это копия объекта, в некотором смысле «более удобная», допускающая манипуляции в пространстве и времени.

Моделированием называется замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели.

Основные этапы математического моделирования

1. Построение модели

На этом этапе выбирается некоторый «нематематический» объект — явление природы, механизм химической реакции, молекулы вещества и т. д. Сначала выявляются основные особенности явления и связи между ними на качественном уровне. Кроме сведений общего характера о природе объекта и целях его исследования, эта стадия может содержать также некоторые предположения (реакция протекает в замкнутом пространстве, парциальные давления веществ постоянны и т. д.). Затем найденные качественные зависимости формулируются на языке математики, то есть строится математическая модель.

1. Решение математической задачи, к которой приводит модель

На этом этапе большое внимание уделяется разработке алгоритмов и численных методов решения задачи на персональном компьютере, при помощи которых результат может быть найден с необходимой точностью и за допустимое время. Для этого осуществляется выбор (или разработка) алгоритма для реализации модели на компьютере. Модель представляется в форме, удобной для применения численных методов, определяется последовательность вычислительных и логических операций, которые нужно произвести, чтобы найти искомые величины с заданной точностью. Вычислительные алгоритмы должны не искажать основные свойства модели и, следовательно, исходного объекта, быть экономичными и адаптирующимися к особенностям решаемых задач и используемых компьютеров.

1. Интерпретация полученных следствий из математической модели

На этом этапе создаются программы, «переводящие» модель и алгоритм на доступный компьютеру язык. К ним предъявляются требования экономичности и адаптивности. Их можно назвать «электронным» эквивалентом изучаемого объекта, уже пригодным для непосредственного испытания на «экспериментальной установке» — компьютере. После проведенных вычислений, получается некоторый результат. Следствия, выведенные из модели на языке математики, интерпретируются на языке, принятом в данной области.

1. Проверка адекватности модели

На этом этапе выясняется, согласуются ли результаты эксперимента с теоретическими (расчетными) следствиями из модели в пределах определенной точности.

В результате исследования модели не только достигается поставленная цель, но и должна быть установлена всеми возможными способами (сравнением с практикой, сопоставлением с другими подходами) ее адекватность – соответствие объекту и сформулированным предположениям. Неадекватная модель может дать результат, сколь угодно отличающийся от истинного, и должна быть либо отброшена, либо соответствующим образом модифицирована.

5. Модификация модели

На этом этапе происходит либо усложнение модели, чтобы она была адекватной действительности, либо ее упрощение ради достижения практически приемлемого решения.

Математическая модель химических процессов, описываемые линейным уравнениям

Пример 1. Какова масса раствора, если масса воды в растворе равна 120 г, а процентное содержание соли в растворе равно 84 %?

Решение

Введем обозначения:

х г – масса всего раствора;

а г – масса воды в растворе;

_ x  a_

г – масса соли в данном растворе;

р % – процентное содержание соли в растворе.

Тогда для определения массы раствора составим пропорцию:

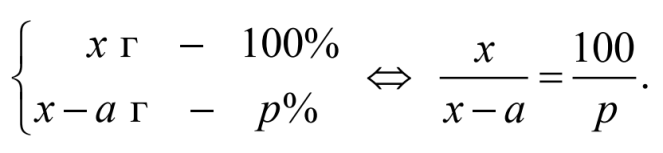
Используя основное свойство пропорции, получим:

p  x 100  _x  a_ или

x  a  x 

p _. 100

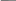Полученное уравнение является математической моделью задачи. Подставим известные числовые данные (а = 120, р = 84 %), раскроем скобки, слагаемые, содержащие неизвестную, перенесем в левую часть уравнения и решим его:

84x 100x  12000

 16x  12000

 x  ¹²⁰⁰⁰  750 г.

16

Ответ: Масса всего раствора составляет 750 г.

Пример 2. Вычислить среднюю скорость химической реакции^*, если через 20 секунд от начала реакции концентрация веществ составляла 0,05 моль/л, а через 40 секунд – 0,04 моль/л.

Решение

Введем обозначения:

t₁ – первоначальное время измерения концентрации вещества;

t₂ – последующее время измерения концентрации вещества;

с₁ – значение концентрации вещества в момент времени t₁; с₂ – значение концентрации вещества в момент времени t₂.

Так как концентрация вещества А в момент времени t₁ измеряется

величиной с₁, а в момент t₂ – величиной с₂, то за промежуток времени

t  t₂  t₁

изменение концентрации вещества составит

c  c₂  c₁ , тогда уравнение для

определения средней скорости химической реакции v будет иметь вид:

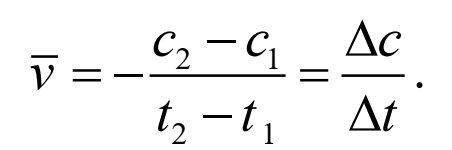
Это уравнение есть математическая модель для определения средней скорости реакции.

Знак минус ставится потому, что, несмотря на убывание концентрации

^* Под скоростью химической реакции понимают изменение концентрации одного из реагирующих веществ в единицу времени при неизменном объеме системы.

вещества А и, следовательно, на отрицательное значение разности c₂  c₁ , скорость реакции может быть только положительной величиной.

Подставляя данные задачи в математическую модель, получаем решение:

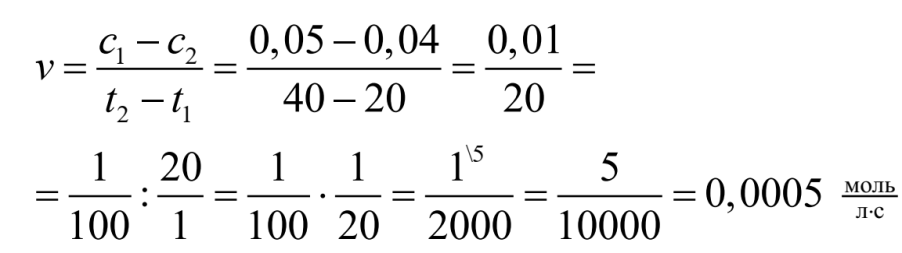
Ответ: Средняя скорость химической реакции равна

0,0005

моль лс

Модели химических процессов, описываемых алгебраическими системами линейных уравнений

Пример 1. К 120 г 15 %- ного раствора соли добавили 80 г воды. Вычислить массовую долю соли во вновь полученном растворе.

Решение

Для решения данной задачи необходимо вычислить сначала массу соли в растворе, а затем ее массовую долю в новом растворе (масса одна и та же в обоих растворах). Говоря математическим языком, в данной задаче две неизвестных величины x и y. Введем обозначения:

М – масса раствора;

р – процентное содержание (массовая доля) соли в исходном растворе;

х – масса соли в растворе;

у – массовая доля соли в новом растворе.

Зная из условия задачи массу исходного раствора и массовую долю соли в нем, можно записать уравнение для нахождения массы соли в растворе (см. предыдущий раздел):

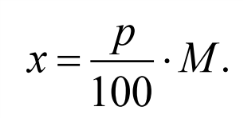
Этот же результат можно получить с помощью составления пропорции:

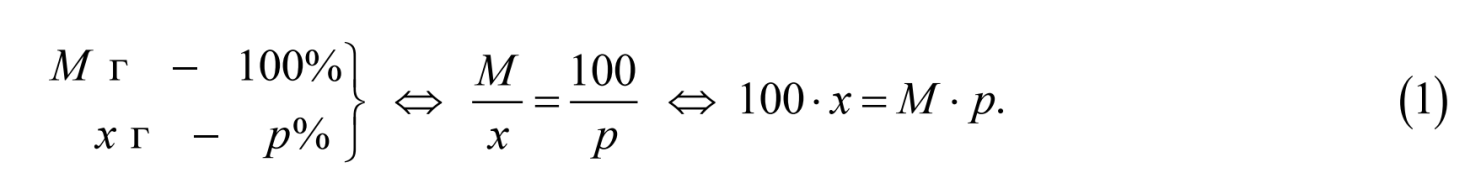
По условию задачи в раствор добавили 80 г воды, т. е. масса раствора стала равной М+80.

Теперь, зная массу нового раствора (М+80) и количество соли (х), составляем уравнение для нахождения массовой доли соли:

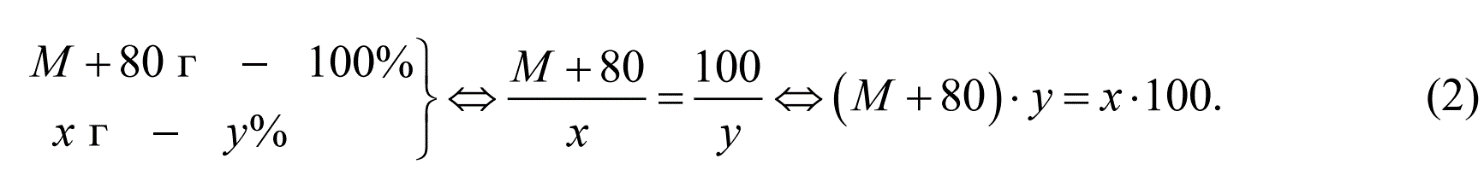
Объединяя уравнения (1) и (2) в систему, получаем математическую модель задачи:

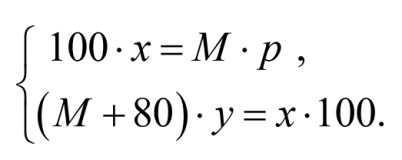
П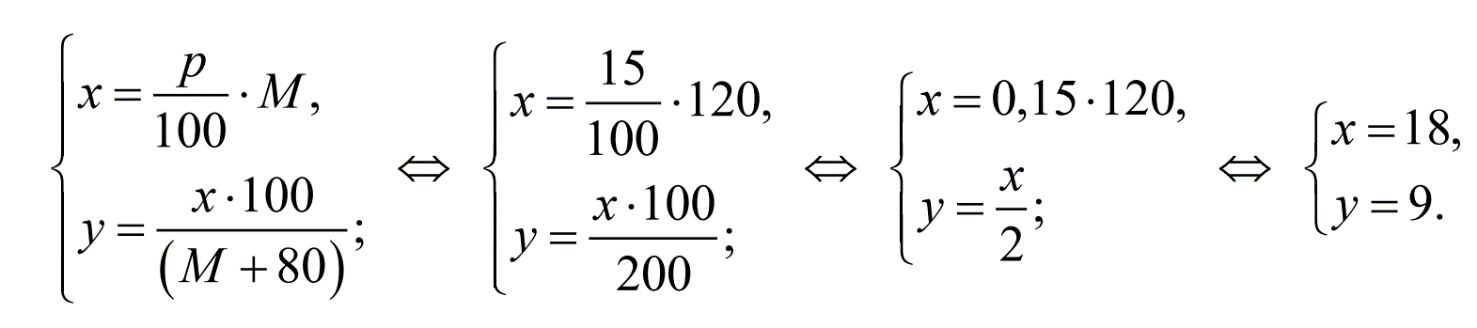 одставляя числовые данные задачи и решая систему из двух линейных уравнений с двумя неизвестными, получим:

Ответ: Массовая доля соли в растворе, полученном добавлением 80 г воды к 120 г 15%-ного раствора соли, равна 9 %.

Пример 2. Имеются два раствора серной кислоты в воде: первый – 40 %-ный, второй – 60 %-ный. Эти два раствора смешали, после чего добавили 5 кг чистой воды и получили 20 %-ный раствор. Если бы вместо 5 кг чистой воды добавили 5 кг 80 %-ного раствора, то получился бы 70 %-ный раствор. Сколько было 40 %-ного и 60 %-ного раствора?

Решение

Введем обозначения: х – масса первого раствора, у – масса второго раствора.

Тогда

 ^{x  y  5} ^{– масса 20 %-ного раствора.}

Так как:

• ^{в х кг 40 %-ного раствора содержится} 0, 4x ^{кг кислоты,}

• в у кг 60 %-ного раствора содержится 0,6 y кг кислоты,

• ^в  ^{x  y  5} ^{кг 20 %-ного раствора содержится}

0,2  _x  y  5_

кг кислоты,

то по условию задачи можно составить первое уравнение:

0,4x  0,6 y  0,2_x  y  5_.

Если вместо 5 кг воды добавить 5 кг 80 %-ного раствора, то получится

^{раствор массой}  ^{x  y  5}^{кг, в котором будет} ^{0,4x  0,6 y  0,8  5}кг кислоты,

^{что составит 70 % от}  ^{x  y  5}кг.

Графические модели

Математические модели бывают не только алгебраическими (в виде неравенств, уравнений). Существуют словесные модели – описание реальных ситуаций словами; графические – модель представляет собой график функции; геометрические – модель представляет собой геометрическую фигуру (например, граф химической реакции – многоугольник). Графические модели часто также называют геометрическими.

Пример 1

Построить график изменения температуры смеси в ходе реакции по ее значениям, полученным с помощью прибора в течение 10 минут. Данные представлены в таблице.

Решение

Построим прямоугольную систему координат. По горизонтальной оси будем откладывать значения времени, а по вертикальной – значения температуры. Отметим на координатной плоскости точки, координатами которых являются числа из таблицы. Всего получается 10 точек. Соединим их плавной линией, в результате получим график температуры.

60

50

40

30

20

10

0

0 1 2 3 4 5 6 7 8 9 10

Построенный график – это математическая модель, описывающая зависимость температуры от времени. Анализируя этот график, можно описать словами, что происходило с температурой смеси во время реакции в течение 10 минут. В течение первой минуты температура резко поднялась до 56 градусов, после чего смесь постепенно стала охлаждаться. На седьмой минуте температура опустилась до 12 градусов и оставалось такой в последующее время. Глядя на график температуры, можно определить, какая и когда была наибольшая температура (56 градусов на первой минуте протекания реакции), когда менялась очень резко (в первые две минуты), когда перестала меняться (после седьмой минуты).

Эта математическая модель относится к графическим.

Часто в задачах по химии требуется графически проиллюстрировать происходящие химические реакции. Преимуществом графического изображения по сравнению с другими способами задания функции являются его наглядность и легкая обозримость.

Пример 2. К 150 г 20 %-ного раствора соли добавили 30 г соли. Определите массовую долю соли в полученном растворе.

Решение

Решение задачи начинаем с построения системы координат. На оси Ох откладываем массу раствора 150 г, на оси Оу – 100 %. Строя перпендикуляры из этих точек, находим точку их пересечения. Соединяем её прямой линией с точкой начала координат.

Для исходного раствора находим массу растворённого вещества (30 г). Затем строим новый отрезок для нового раствора, полученного в результате добавления соли к исходному. На оси Ох от точки, соответствующей массе исходного раствора, откладываем вправо 30 г (масса добавленной соли). Это масса полученного раствора. Восстанавливаем из неё перпендикуляр до пересечения с прямой, проходящей через отметку 100 % на оси Оу. Точку их пересечения соединяем с началом координат – получаем отрезок, соответствующий новому раствору (показан пунктирной линией). На оси Ох от точки, показывающей массу соли в первом растворе, откладываем вправо 30 г (масса добавленной соли) и получаем массу соли во втором растворе. Восстанавливаем из неё перпендикуляр до пересечения с пунктирным отрезком, а из точки пересечения – перпендикуляр на ось Оу. Значение равно массовой доле соли во втором растворе.

Таким образом, математическая модель рассматриваемой задачи представима в следующем графическом виде:

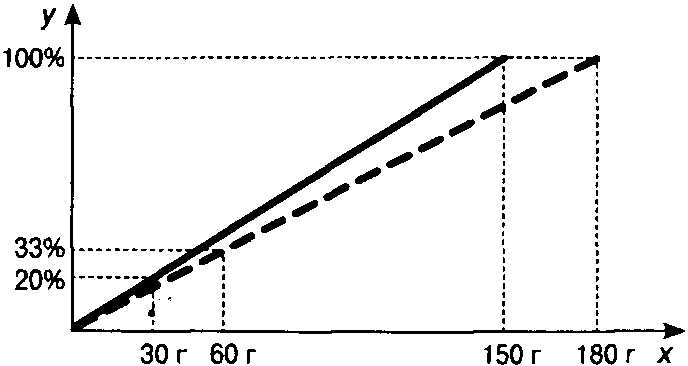
Ответ: Массовая доля соли равна 33 %.

Порядок выполнения работы

Решите в тетради для практических работ предложенные задачи используя математическое моделирование

1. К 200 г 4 %-ного раствора сахара добавили 5 г сахара. Определить массовую долю вещества в полученном растворе.

2. К 80 г раствора с неизвестной массовой долей вещества добавили 40 г воды. Вычислить массовую долю соли в исходном растворе, если после разбавления она стала равна 18 %.

3. Смешали 30 %-ный раствор соляной кислоты с 10 %-ным и получили 600 г 15 %-ного раствора. Сколько граммов 10 %-ного раствора было взято?

4. В замкнутый сосуд вместимостью 5 л помещены водород массой 0,8 г и хлор. Через 10 с в результате реакции масса водорода снизилась до 0,3 г. Вычислите среднюю скорость реакции.

5. Построить график изменения температуры смеси в ходе реакции по ее значениям, полученным с помощью прибора в течение 10 секунд. Данные представлены в таблице.

   Время, мин	0	1	2	3	4	5	6	7	8	9	10
   Температура, Со	5	15	24	26	30	20	18	14	8	4	4

6. С помощью составления графической модели решить задачу:

К 250 г 40 %-ного раствора соли добавили 70 г соли. Определите массовую долю соли в полученном растворе.