Математический маятник

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТРЛІГІ

Жамбыл облысы. Дарынды ер балаларға арналған мамандандырылған

қазақ-түрік мектеп-интернаты

Тақырыбы: Математикалық маятник (Simple pendulum)

Пәні: Физика

Орындаған: Жумадилов Ержан Есетұлы

Тараз 2016

Simple pendulum

LESSON: Physics

CLASS: 9A

Subject: Simple pendulum

MAIN AIM: Understanding concepts of simple pendulum

LESSON OBJECTIVES: Students should be able to understand the basic ideas of damping and resonance

Review of the previous lesson:

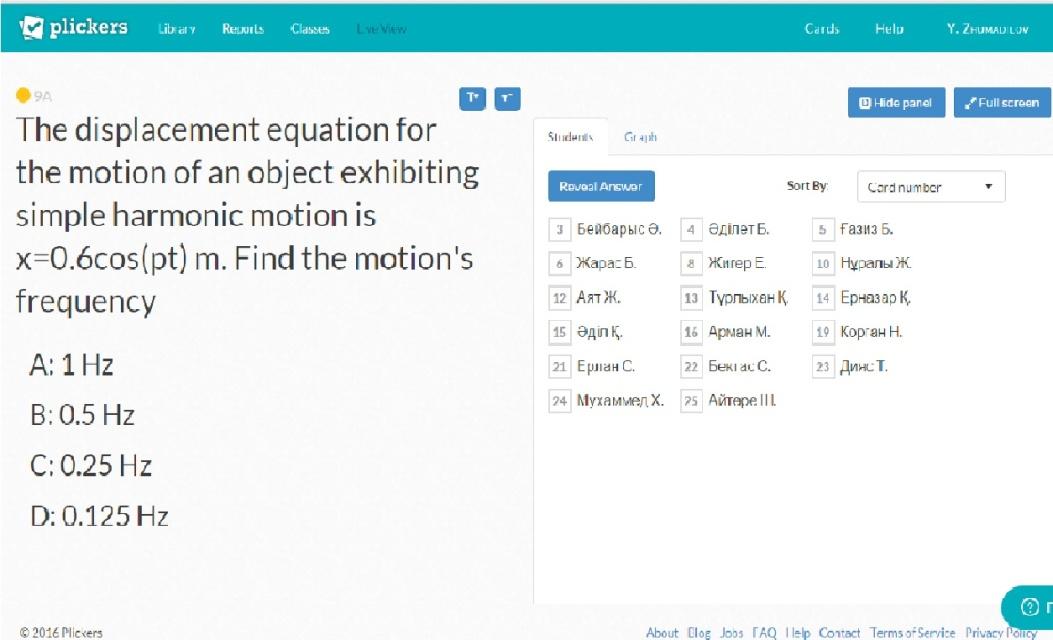
The displacement equation for the motion of an object exhibiting simple harmonic motion is x=0.6cos(pt) m. Find the motion's frequency.

The displacement equation for the motion of an object exhibiting simple harmonic motion is x=0.6cos(pt) m. Find the motion's angular speed.

The displacement equation for the motion of an object exhibiting simple harmonic motion is x=0.6cos(pt) m. Find the motion's amplitude.

An object is exhibiting simple harmonic motion along the y-axis. The equation for its position as a function of time is y=0.4 sin (2.5pt) m. Find the position of the object.

New topic:

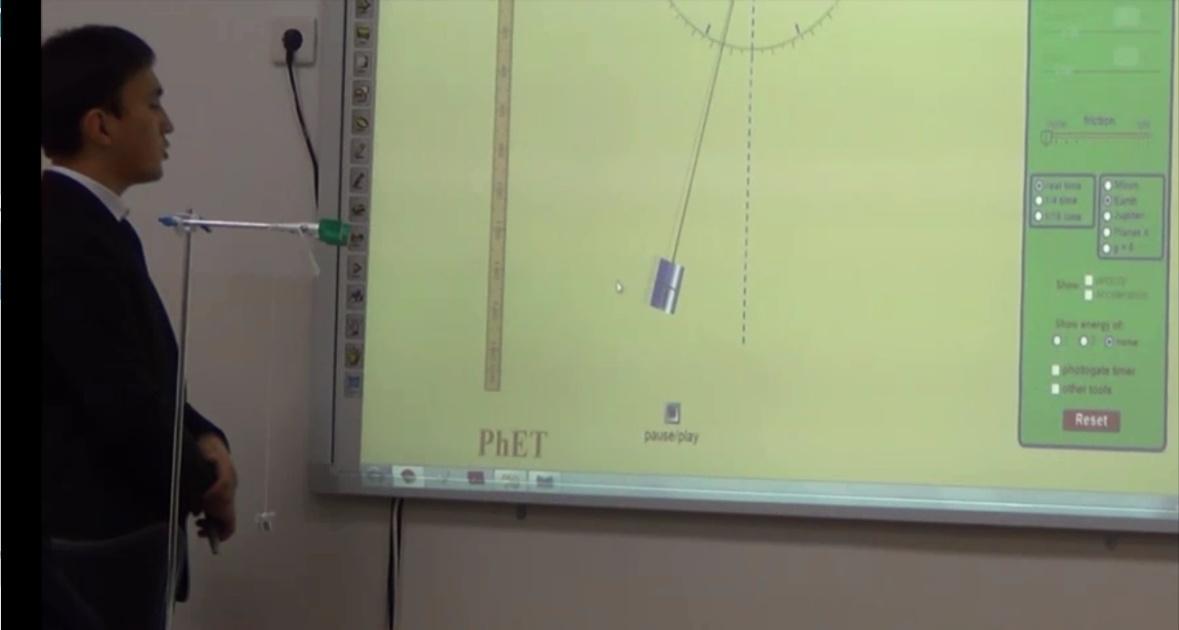
A simple pendulum consists of a small mass, called a bob, suspended by a light

and non-elastic string of length L, attached to a rigid support. When the mass is

pulled to one side of its equilibrium position through a small angle θ and released,

as shown in Figure 4.4.1, the simple pendulum performs simple harmonic

motion. A child on a swing and a grandfather clock are some examples of simple

pendulums. The simple harmonic motion of a simple pendulum will be analysed

and an expression found for its period.

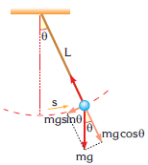
During the motion of the bob, the gravitational force acting on its mass has a component along the string and another component perpendicular to the string. The perpendicular component provides the restoring force.

The negative sign indicates that the restoring force, ÁFres, is in the opposite direction to the displacement, s.

The displacement, s, from the equilibrium position is the length along the arc

through which the mass swings. It is given by

The restoring force is proportional to displacement through the equation

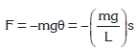
The following expression is obtained for the period of the simple pendulum

Homework: Exercises 27-54, page 129