Тригонометрическое уравнение с ОДЗ (1+cosx)(1sinx−1)=0.
Важное отличие в этом примере, что в знаменателе появился синус.
Хотя мы немного решали подобные уравнения в предыдущих уроках, стоит остановиться на ОДЗ поподробнее.
ОДЗ sinx≠0⇒x≠πk. Когда мы будем отмечать решение на круге, эту серию корней мы отметим специально проколотыми (открытыми) точками, чтобы показать, что x не может принимать такие значения.
Решение Приведем к общему знаменателю, а затем поочередно приравняем обе скобки к нулю. (1+cosx)(1−sinxsinx)=0, 1+cosx=0 или 1−sinxsinx=0, cosx=−1 или sinx=1.

1. а) Решите уравнение 5cosx+4/4tgx-3=0
б) Найдите все корни этого уравнения, принадлежащие отрезку [-4п,-5п/2]
2. Решите уравнение: 2sin2x-5sinx-3/√x+п/6=0
3. Решите уравнение: 4cos2x+8sinx-7/√tgx=0
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



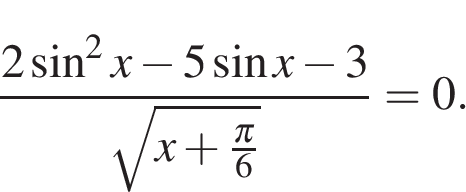









 Материал по математике "Тригонометрические уравнения, исследование ОДЗ" (72.99 КB)
Материал по математике "Тригонометрические уравнения, исследование ОДЗ" (72.99 КB)
 0
0 3458
3458 453
453 Нравится
0
Нравится
0




