Не всегда можно полностью разделить одно число на другое. В примерах на деление может оставаться остаток. Такое деление называется деление с остатком.
Деление с остатком - это деление одного натурального числа на другое, при котором остаток не равен нулю.
Если при делении натуральных чисел остаток равен нулю, то говорят, что делимое делится на делитель без остатка, или, иначе говоря, делится нацело.
Деление с остатком записывают так:
17 (делимое) : 3 (делитель) = 5 (неполное частное) ОСТ (2)
Читается пример следующим образом:
17 разделить на 3 получится 5 и остаток 2.
Порядок решения примеров на деление с остатком.
1. Находим наибольшее число до 17, которое делится на 3 без остатка. Это 15.
15 : 3 = 5
2. Вычитаем из делимого найденное число из пункта 1.
17 - 15 = 2
3. Сравниваем остаток с делителем. 2<3
При делении с остатком остаток всегда должен быть меньше делителя.
Если получилось, что остаток больше делителя, значит, вы неверно нашли наибольшее число, которое делится на делитель без остатка.

4. Записываем ответ.
17 : 3 = 5 ост (2)
При решении более сложных примеров не всегда можно легко найти наибольшее число из пункта 1. Иногда для этого необходимо произвести дополнительные расчёты в столбик. Покажем это на примере.
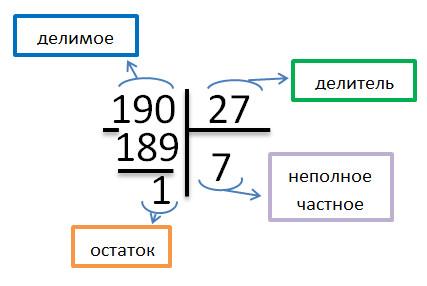
190 : 27 =
Методом подбора найдём на сколько надо умножить 27, чтобы получить ближайшее число к 190.
Попробуем умножить на 6.
27 * 6 = 162
Рассчитаем остаток и сравним его с делителем.
190 - 162 = 28
28 (остаток) > 27(делитель)
Остаток больше делителя. Это означает, что 6 как множитель нам не подходит. Попробуем умножить делитель на 7.
27 * 7 = 189
Снова рассчитаем и сравним остаток с делителем.
190 - 189 = 1.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход

















 Материал по математике на тему "Деление с остатком" (0.12 MB)
Материал по математике на тему "Деление с остатком" (0.12 MB)
 0
0 2030
2030 17
17 Нравится
0
Нравится
0





