Математика без границ (внеклассное мероприятие)

Цель: развивать математические способности, сообразительность, любознательность, логическое мышление, укреплять память учащихся; развивать коммуникативные возможности учащихся в процессе подготовки и проведения внеклассных мероприятий по предмету; расширять кругозор учащихся.

ХОД МЕРОПРИЯТИЯ

Ведущая.

- Выдающийся французский ученый XVII века Блез Паскаль писал: «Предмет математики столь серьёзен, что не следует упускать ни одной возможности сделать его более занимательным».

Сегодня мы собрались на математический конкурс – «Математика без границ». Все вопросы, которые будут заданы, связаны с математикой.

-Мы постараемся доказать, что математику не зря называют «царицей наук», что ей больше, чем какой-либо другой науке свойственны красота, гармония, изящество и точность.

1. Представляем наше жюри…

А теперь каждый капитан представит свою команду. . .

2. Конкурс « Разминка» Каждой команде предстоит ответить на 10 вопросов.

Вопросы 1 команде:

1. Сумма углов в треугольнике

2. Значение переменной при решении уравнения

3. Чему равен 1 пуд

4. На какой угол поворачивается солдат по команде «кругом»

5. Дробь, меньшая 1 называется

6. График квадратичной функции.

7. Результат деления

8. Сумма длин сторон многоугольника

9. Самое маленькое трехзначное число

10. Прямые, которые не пересекаются

Вопросы 2 команде:

1. Математическое предложение, не требующее доказательств

2. Наименьшее натуральное число

3. Луч, делящий угол пополам

4. Чему равна четверть часа

5. Сколько цифр в математике

6. Результат сложения

7. Треугольник, у которого две стороны равны

8. Направленный отрезок.

9. Наибольшее целое отрицательное число

10. Отношение противолежащего катета к гипотенузе

Вопросы 3 команде:

1. Луч, делящий угол пополам

 2. Сумма одночленов

3. Четырехугольник, у которого только две стороны параллельны, а две другие -нет

4. Сотая часть числа

5. Инструмент для построения окружности

6. График линейной функции

7. Равенство двух отношений

8. Единица измерения угла

9. Результат вычитания

10. Самая большая хорда окружности

Полную информацию смотрите в файле. 

ДАГЕСТАН г. КИЗИЛЮРТ

МКОУ СОШ №7

ВНЕКЛАССНОЕ МЕРОПРИЯТИЕ

по математике

для учащихся 9 классов

« Математика

без границ»

Подготовила и провела Магомедова Е. М.

Цель: развивать математические способности, сообразительность, любознательность, логическое мышление, укреплять память учащихся; развивать коммуникативные возможности учащихся в процессе подготовки и проведения внеклассных мероприятий по предмету; расширять кругозор учащихся.

Оборудование:

Портреты ученых- математиков;

Плакаты и математические газеты;

Карточки с заданиями;

Слайды

План:

1. Представление жюри и команд-участников.

2.Разминка.

3.Конкурс « Великие ученые».

4.Конкурс «Эрудиты».

5.Конкурс капитанов (ассоциация).

6. Игра со зрителями.

7.Логическая задача.

8.Аукцион математических терминов.

9. Подведение итогов, награждение победителей.

ХОД МЕРОПРИЯТИЯ

Ведущая.

- Выдающийся французский ученый XVII века Блез Паскаль писал: «Предмет математики столь серьёзен, что не следует упускать ни одной возможности сделать его более занимательным».
Сегодня мы  собрались на математический конкурс – «Математика без границ». Все вопросы, которые будут заданы, связаны с математикой.

-Мы постараемся доказать, что математику не зря называют «царицей наук», что ей больше, чем какой-либо другой науке свойственны красота, гармония, изящество и точность.  

1.Представляем наше жюри…

А теперь каждый капитан представит свою команду...

2. Конкурс « Разминка» Каждой команде предстоит ответить на 10 вопросов.

Вопросы 1 команде:

1.Сумма углов в треугольнике

2.Значение переменной при решении уравнения

3.Чему равен 1 пуд

4.На какой угол поворачивается солдат по команде «кругом»

5. Дробь, меньшая 1 называется

6.График квадратичной функции.

7.Результат деления

8.Сумма длин сторон многоугольника

9.Самое маленькое трехзначное число

10.Прямые, которые не пересекаются

Вопросы 2 команде:

1.Математическое предложение, не требующее доказательств

2.Наименьшее натуральное число

3.Луч, делящий угол пополам

4.Чему равна четверть часа

5.Сколько цифр в математике

6.Результат сложения

7.Треугольник, у которого две стороны равны

8.Направленный отрезок.

9.Наибольшее целое отрицательное число

10.Отношение противолежащего катета к гипотенузе

Вопросы 3 команде:

1.Луч, делящий угол пополам

2.Сумма одночленов

3.Четырехугольник, у которого только две стороны параллельны, а две другие -нет

4.Сотая часть числа

5.Инструмент для построения окружности

6.График линейной функции

7.Равенство двух отношений

8.Единица измерения угла

9.Результат вычитания

10.Самая большая хорда окружности

 Вопросы 4 команде:

1.Отрезок, соединяющий две точки окружности

2.Инструмент для измерения углов на плоскости

3.Предложение, истинность которого нужно доказать

4.Число «пи» равно…

5.Графиком обратной пропорциональности является …

6.Количество делителей простого числа

7. Как называется число, которое делится на 2

8.Результат умножения

9.Угол, величина которого меньше 90º

10.Параллелограмм, у которого все стороны равны

3 конкурс «Великие ученые»

Перед вами портреты великих математиков. Вы должны ответить, о ком из них идет речь:

1)Многие знаменитые математики мира на протяжении 20 веков старались решить величайшую проблему : «Сколько прямых, параллельных данной, можно провести через заданную точку?» Кто разрешил эту проблему? ( Н.И. Лобачевский.)

2) Математик, революционер, умерший в 21 год, погиб на дуэли. ( Э. ГАЛУА)

3)У этого крупнейшего математика 19 века рано проявились математические способности. Рассказывают, что в трехлетнем возрасте он заметил ошибку в расчетах отца- бухгалтера. В семь лет он пошел в школу. В то время в одной комнате занимались ученики разных классов. И чтобы занять первоклассников учитель предложил им сложить числа от 1 до 100. Не успев объяснить тему 3 классу , учитель услышал правильный ответ. Назовите имя будущего великого математика (Карл Гаусс)

4) Девизом каждого, кто нашел что-то новое, является слово «эврика!» Так воскликнул ученый, открыв новый закон. Он же с большой точностью вычислил значение числа пи.(Архимед)

5)Кто из ученых участвовал в атлетических состязаниях и на олимпийских играх был дважды увенчан лавровым венком за победу в кулачном бою? (Пифагор).

4 конкурс « Эрудиты»

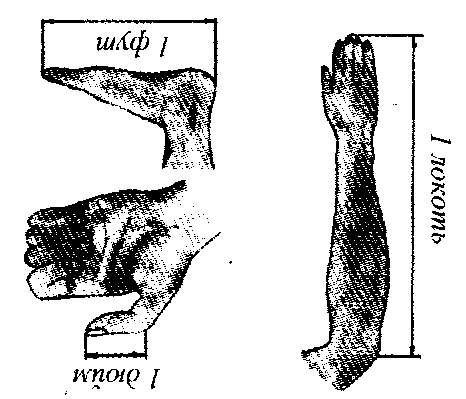
1) Меры длины: локоть, дюйм, фунт, фут.

а) Найдите среди них лишнее слово (фунт-мера веса)

б) Расположите единицы в порядке возрастания

в) Покажите на себе , как определяются эти величины и чему примерно равно их численное значение

1 локоть ≈ 46 см

1 дюйм ≈ 2,5 см

1 фут ≈ 30 см

2) Четырехугольники : квадрат, параллелограмм, трапеция, прямоугольник.

а)Какой четырёхугольник по очень важному признаку явля­ются лишним?

( Трапеция. Все эти четырёхугольники, кроме трапеции, являются парал­лелограммами, так как у них противолежащие стороны попарно па­раллельны.)

б) Какая из этих фигур обладает наибольшим количеством свойств?

( Квадрат.)

в

Для какого четырёхугольника имеет смысл выражение «Найдите среднюю линию»? (Трапеция.)

г) Название какой фигуры в переводе с греческого языка означает «обеденный столик»? (Трапеция.)

3) Кривые: перед вами четыре кривые.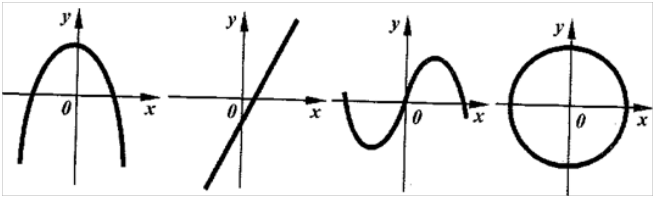

а) Я утверждаю, что все они являются графиками некоторых функций. Так ли это? ( Окружность не является графиком функции.)

б) На каком рисунке представлен график квадратичной функции?(№ 1.)

в)На каком рисунке изображен график возрастающей на всей области определения функции? (№2)

г) Квадратичная функция.

Перед вами квадратичные функции, графиками которых являются параболы.

1) у = - х² – 7х + 3

2) у = - 1 + 3х + 7х²

3) у = - (х + 7)² – 3

4) у = 3 - 7х²

а) Верно ли, что ветви всех парабол направлены вниз? (Нет, у № 2 - вверх.)

б) Вершина какой параболы находится в точке с координатами (0;3)? (№4)

в) Осью симметрии какой параболы является прямая х = —7? (№3.) г) Какую из парабол можно получить из графика функции у = х² с помощью двух параллельных переносов: вдоль оси абсцисс на 7 ед. влево и вдоль оси ординат на 3 ед. вниз? (№3)

5.Конкурс капитанов (ассоциация).

Каждому капитану выдается листок, на котором написано слово. Капитан должен написать на этом листке 8 слов , ассоциативно связанных с данным словом. Команде дается такое же задание. Листки сдаются жюри. Побеждает та команда, у которой получится больше совпадений.

6.Игра со зрителями.

1) Назовите среднее арифметическое женщины и рыбы? (русалка)

2) Назовите среднее арифметическое ежа и змеи (колючая проволока)

3)Назовите среднее арифметическое мужчины и коня (кентавр)

4) Что есть у каждого слова, растения и уравнения? (корень)

5) Эмблемой какого автомобиля являются четыре кольца? (Ауди)

.

7.Логическая задача.

Карлсон попросил у Малыша малино­вого варенья. На полке стояли три банки с вареньем. На первой было написано «Клубничное или малиновое», на второй «Вишневое», а на третьей «Малиновое». В какой из них находит­ся малиновое варенье, если известно, что фрекен Бок все надписи перепутала?

Ответ: малиновое варенье находится во второй банке.

Малыш рассуждал так: на первой банке надпись «Клубничное или малиновое», но все надписи неверны, поэтому в ней не может на­ходиться ни клубничное, ни малиновое варенье. В третьей банке то­же не может быть малинового варенья, так как на ней надпись «Ма­линовое». Следовательно, малиновое варенье находится во второй банке.

8. Аукцион математических терминов.

Из слова «арифметика» нужно составить как можно больше слов. Каждую букву разрешается использовать столько раз, сколько она встречается в этом слове, т.е. буквы «а» и «и» - два раза, а осталь­ные - по одному. На вы­полнение задания отводится 1 минута.

9. Подведение итогов, награждение победителей.