Мастер-класс по информатике "Моделирование поразрядных вычислений в различных системах счисления в среде электронных таблиц"

Материал можно использовать при проведении факультатива, элективного курса, в исследовательской или проектной работе с учениками.

Одна из актуальных тем курса информатики – тема «Системы счисления». Знание этого материала помогает приобретать навыки оперирования единицами измерения информации, понимать, каким образом передается и в каком виде хранится информация в памяти компьютера, овладевать понятиями «бит», «байт», «кодирование информации в компьютере».

ПРОБЛЕМА.

Почему в современных компьютерах используется двоичная система счисления и можно ли заменить ее какой-либо другой?

Почему компьютер обрабатывает только двоичные данные, но при этом является универсальным исполнителем?

Сможем ли мы в процессе моделирования поразрядных вычислений в различных системах счисления найти ответы на вопрос, какую роль сыграли системы счисления в истории компьютеров?

Результаты...

Выбор табличного процессора, как программного средства для моделирования поразрядных вычислений в различных системах счисления связан с тем, что именно среда электронной таблицы наиболее наглядно может представить работу в каждом разряде. Отображение формул в данном случае будет помогать лучше разобраться в математических и логических операциях с разрядами. Отправной точкой берем десятичную систему счисления и реализуем способ сложения и вычитания двух натуральных чисел столбиком.

Выполнение арифметических операций в различных системах счисления проводятся по правилам, аналогичным известным нам для десятичной системы. Правила эти следующие:

- арифметические операции сложения и вычитания проводятся поразрядно, то есть каждый разряд одного числа складывается (вычитается) с разрядом того же веса другого числа;

- если при выполнении операции над разрядами получается число большее чем основание системы счисления, то говорят, что возникает перенос, который учитывается при выполнении операции с более старшим разрядом;

- если при выполнении операции вычитания уменьшаемый разряд меньше вычитаемого возникает заем, который уменьшает на 1 более старший разряд уменьшаемого;

- умножение проводится поразрядным умножением со сложением получаемых результатов;

1 эксперимент. Поразрядное сложение десятичных чисел.

Сформулируем правило поразрядного сложения чисел:

Сложение чисел начинается с цифр наименьшего разряда; если при сложении цифр разряда полученное число больше либо равно 10 (основанию системы счисления), то определяется, какое количество единиц остается в этом разряде, а какое переносится в следующий разряд. После обработки цифр разряда происходит переход к обработке цифр следующего (соседнего слева) разряда.

1. Ввод числовых данных. Нужно сложить два девятиразрядных числа.

В ячейки поразрядно заносятся цифры первого и второго чисел.

2. Ввод формул.

- подсчитывается сумма цифр наименьшего разряда и значение переноса в следующий разряд. Если сумма двух цифр больше либо равна основанию системы счисления(10), то из суммы цифр вычитается 10.

Таким образом, получается формула:

=ЕСЛИ(K3+K4<10;K3+K4;K3+K4-10), а формула подсчета единиц, переносимых в следующий разряд:

=ЕСЛИ(K3+K4<10;0;1)

- Для подсчета суммы цифр следующего разряда формула изменяется:

=ЕСЛИ(J3+J4+K7<10;J3+J4+K7;J3+J4+K7-10)

Меняется и формула подсчета единиц, переносимых в следующий разряд:

=ЕСЛИ(J3+J4+$K$7<10;0;1)

Формулы копируем для остальных разрядов, проверяем, не появился ли в числе-результате десятый разряд. Для этого в ячейку В5 заносим формулу =ЕСЛИ($C$7>0;$C$7;"")

Тестирование.

Проверяем перенос из одного разряда в другой:

999999999+111111111=1111111110

899999999+2=900000001

2 эксперимент. Поразрядное вычитание из одного натурального числа другое.

Сформулируем правило поразрядного вычитания чисел:

Вычитание чисел начинается с цифр наименьшего разряда, если цифра разряда первого числа меньше цифры соответствующего разряда второго числа, то из соседнего слева разряда занимается единица. После обработки цифр разряда происходит переход к обработке цифр следующего разряда.

Запись исходных данных.

Пусть первое число девятиразрядное, второе не превышает девяти разрядов.

Находим разность цифр наименьшего разряда и значение переноса в следующий разряд. При написании формулы учтем, что если цифра разряда первого числа меньше цифры соответствующего разряда второго числа, то из старшего разряда занимается единица. 

Весь материал - в документе.

Овчинникова И.И., учитель информатики и ИКТ МОУ гимназии №12 Краснооктябрьского района г. Волгограда

Мастер-класс

«Моделирование поразрядных вычислений в различных системах счисления в среде электронных таблиц»

Материал можно использовать при проведении факультатива, элективного курса, в исследовательской или проектной работе с учениками.

Одна из актуальных тем курса информатики – тема «Системы счисления». Знание этого материала помогает приобретать навыки оперирования единицами измерения информации, понимать, каким образом передается и в каком виде хранится информация в памяти компьютера, овладевать понятиями «бит», «байт», «кодирование информации в компьютере».

ПРОБЛЕМА

• Почему в современных компьютерах используется двоичная система счисления и можно ли заменить ее какой-либо другой?

• Почему компьютер обрабатывает только двоичные данные, но при этом является универсальным исполнителем?

• Сможем ли мы в процессе моделирования поразрядных вычислений в различных системах счисления найти ответы на вопрос, какую роль сыграли системы счисления в истории компьютеров?

Результаты

Выбор табличного процессора, как программного средства для моделирования поразрядных вычислений в различных системах счисления связан с тем, что именно среда электронной таблицы наиболее наглядно может представить работу в каждом разряде. Отображение формул в данном случае будет помогать лучше разобраться в математических и логических операциях с разрядами. Отправной точкой берем десятичную систему счисления и реализуем способ сложения и вычитания двух натуральных чисел столбиком.

Выполнение арифметических операций в различных системах счисления проводятся по правилам, аналогичным известным нам для десятичной системы. Правила эти следующие:

• арифметические операции сложения и вычитания проводятся поразрядно, то есть каждый разряд одного числа складывается (вычитается) с разрядом того же веса другого числа;

• если при выполнении операции над разрядами получается число большее чем основание системы счисления, то говорят, что возникает перенос, который учитывается при выполнении операции с более старшим разрядом;

• если при выполнении операции вычитания уменьшаемый разряд меньше вычитаемого возникает заем, который уменьшает на 1 более старший разряд уменьшаемого;

• умножение проводится поразрядным умножением со сложением получаемых результатов;

1 эксперимент. Поразрядное сложение десятичных чисел

Сформулируем правило поразрядного сложения чисел:

Сложение чисел начинается с цифр наименьшего разряда; если при сложении цифр разряда полученное число больше либо равно 10 (основанию системы счисления), то определяется, какое количество единиц остается в этом разряде, а какое переносится в следующий разряд. После обработки цифр разряда происходит переход к обработке цифр следующего (соседнего слева) разряда.

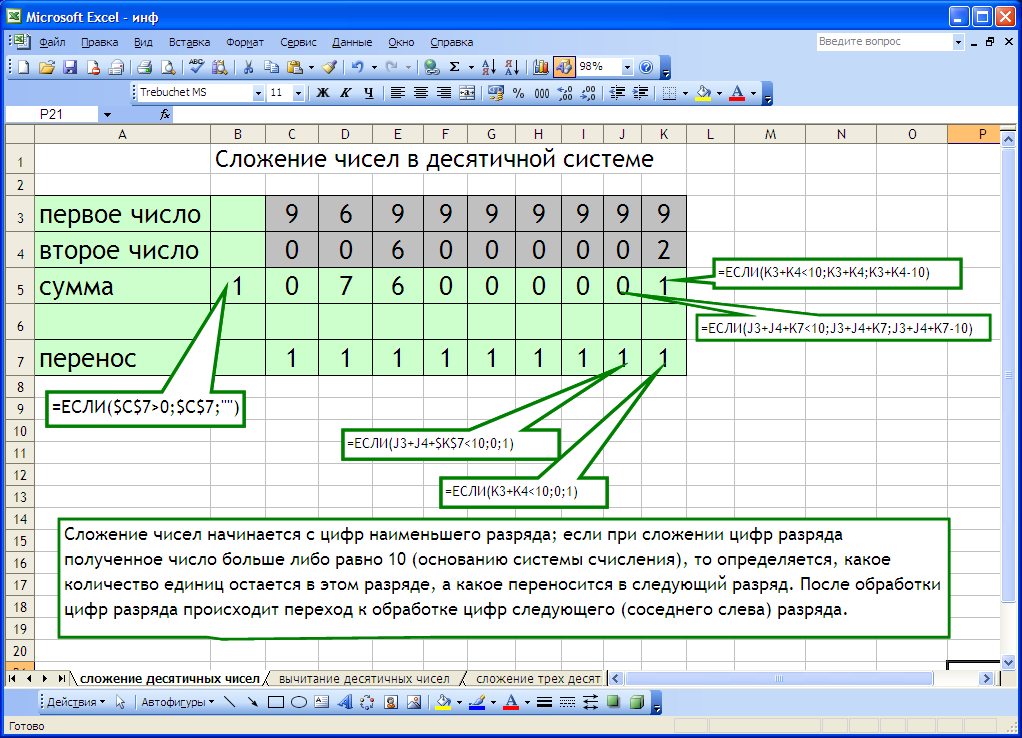
1. Ввод числовых данных. Нужно сложить два девятиразрядных числа.

В ячейки поразрядно заносятся цифры первого и второго чисел.

2. Ввод формул.

- подсчитывается сумма цифр наименьшего разряда и значение переноса в следующий разряд. Если сумма двух цифр больше либо равна основанию системы счисления(10), то из суммы цифр вычитается 10.

Таким образом, получается формула

=ЕСЛИ(K3+K4

а формула подсчета единиц, переносимых в следующий разряд

=ЕСЛИ(K3+K4

- Для подсчета суммы цифр следующего разряда формула изменяется

=ЕСЛИ(J3+J4+K7

Меняется и формула подсчета единиц, переносимых в следующий разряд

=ЕСЛИ(J3+J4+$K$7

Формулы копируем для остальных разрядов, проверяем, не появился ли в числе-результате десятый разряд. Для этого в ячейку В5 заносим формулу =ЕСЛИ($C$70;$C$7;"")

1. Тестирование

Проверяем перенос из одного разряда в другой

999999999+111111111=1111111110

899999999+2=900000001

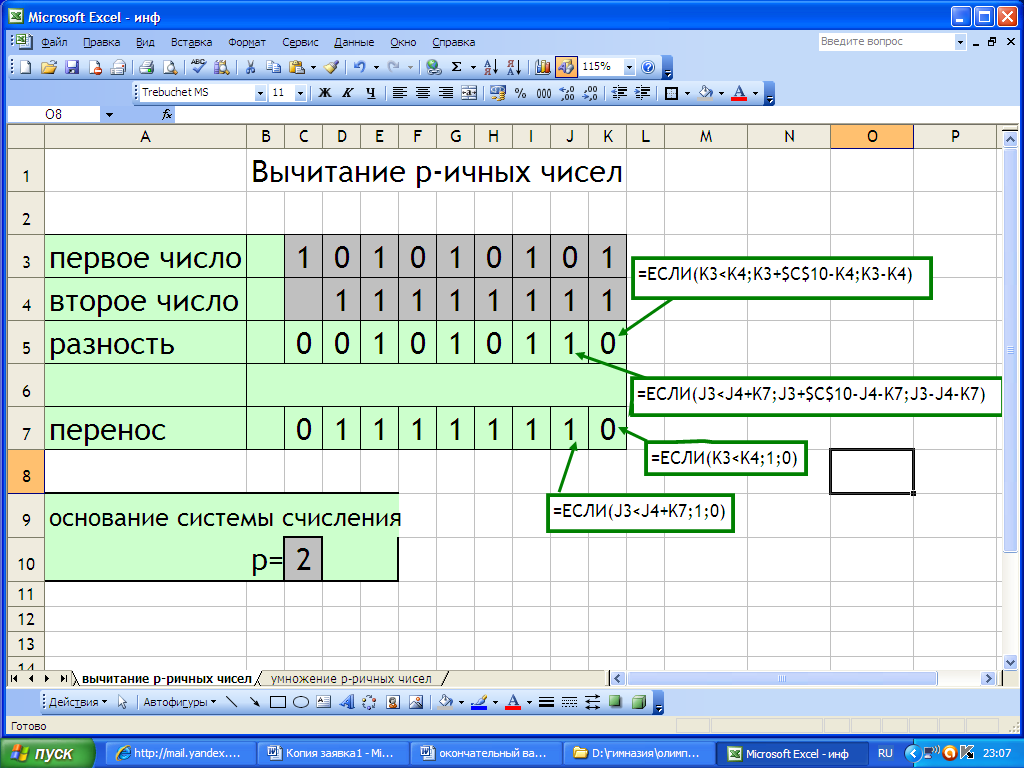
2 эксперимент. Поразрядное вычитание из одного натурального числа другое.

Сформулируем правило поразрядного вычитания чисел:

Вычитание чисел начинается с цифр наименьшего разряда, если цифра разряда первого числа меньше цифры соответствующего разряда второго числа, то из соседнего слева разряда занимается единица. После обработки цифр разряда происходит переход к обработке цифр следующего разряда.

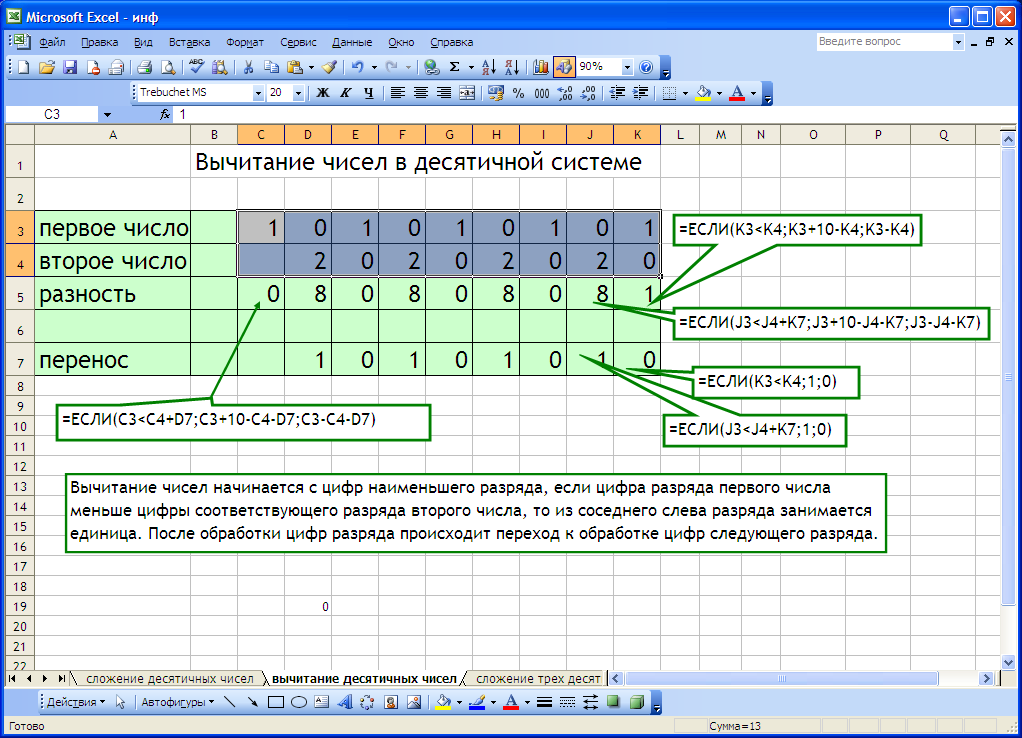
1. Запись исходных данных

2. Пусть первое число девятиразрядное, второе не превышает девяти разрядов.

3. Находим разность цифр наименьшего разряда и значение переноса в следующий разряд. При написании формулы учтем, что если цифра разряда первого числа меньше цифры соответствующего разряда второго числа, то из старшего разряда занимается единица.

=ЕСЛИ(K3

Формула о заеме единиц из старшего разряда

=ЕСЛИ(K3

1. Для подсчета разности цифр следующего разряда

=ЕСЛИ(J3

Изменяется и формула о заеме единиц из старшего разряда

=ЕСЛИ(J3

1. Для последнего разряда проверим условие для отбрасывания незначащего нуля

=ЕСЛИ(C3-C4-D7=0;"";C3-C4-D7)

1. Тестирование

Необходимо учесть заем единиц из старшего разряда

111111111-99999999=11111112

101010101-20202020=80808081

100000000-99999999=1

3 эксперимент

Мы реализовали случаи выполнения арифметических операций над числами конкретной (десятичной) системы счисления. Ответим на вопрос: как изменится решение задачи, если складываются не два, а несколько десятичных чисел?

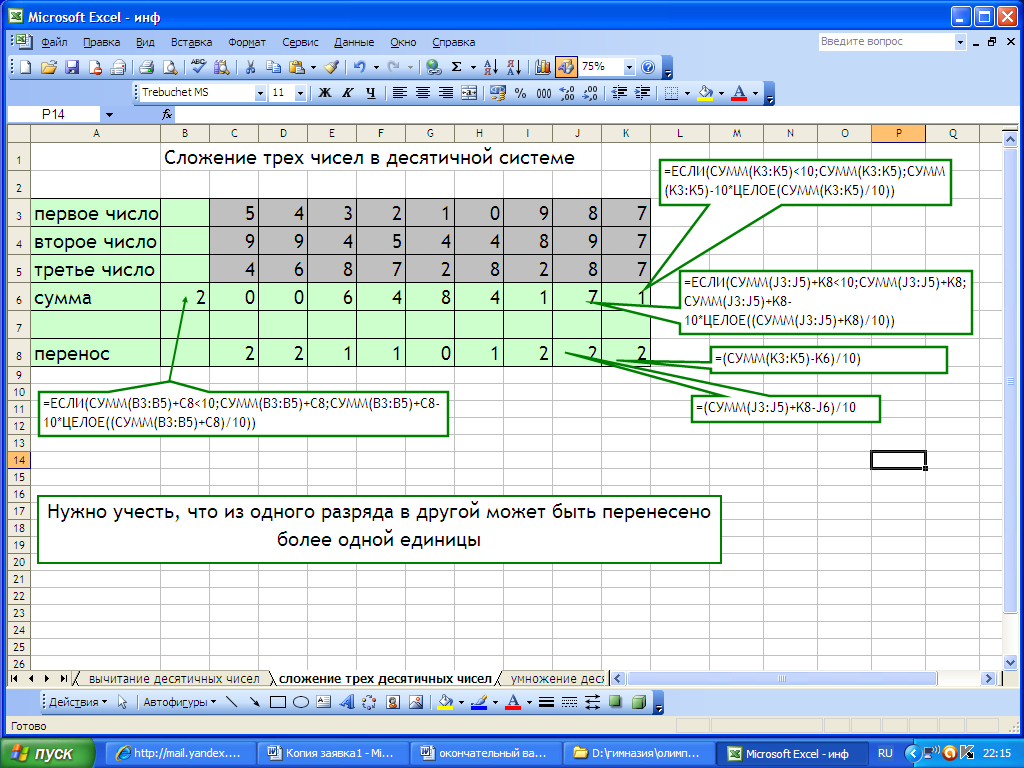
Прежде всего, нужно учесть, что из одного разряда в другой может быть перенесено более одной единицы.

Сумма =ЕСЛИ(СУММ(K3:K5)

Перенос =(СУММ(K3:K5)-K6)/10

Сумма следующего разряда =ЕСЛИ(СУММ(J3:J5)+K8

Перенос следующего разряда =(СУММ(J3:J5)+K8-J6)/10

4 эксперимент

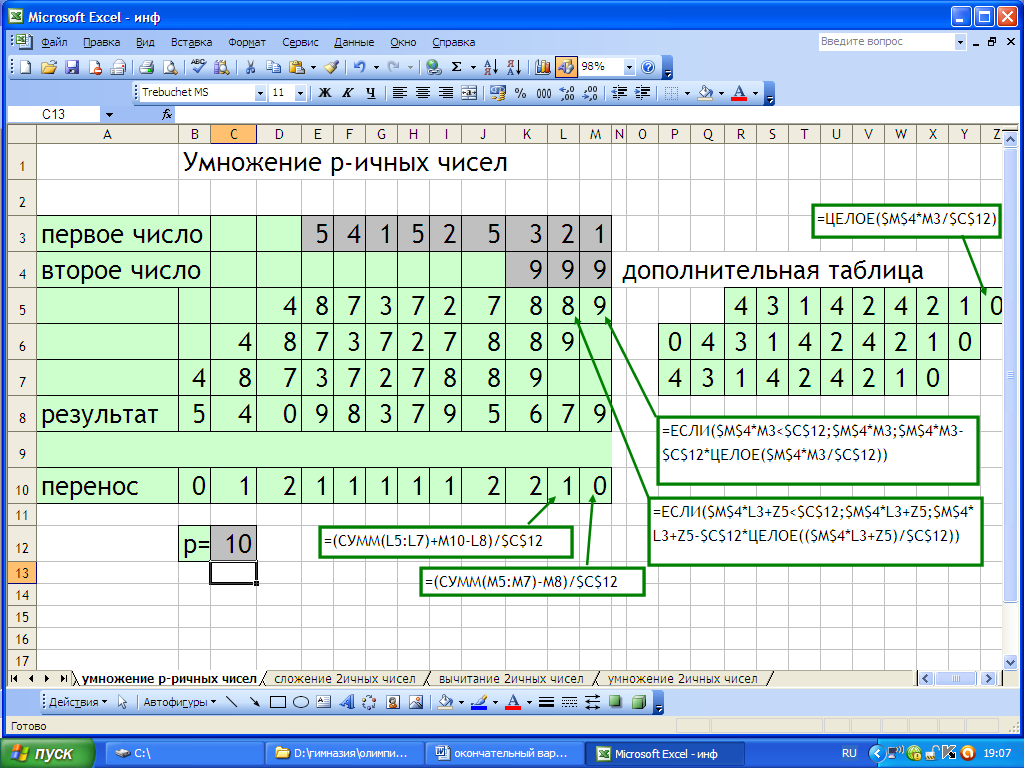
Реализуем поразрядное умножение двух натуральных десятичных чисел

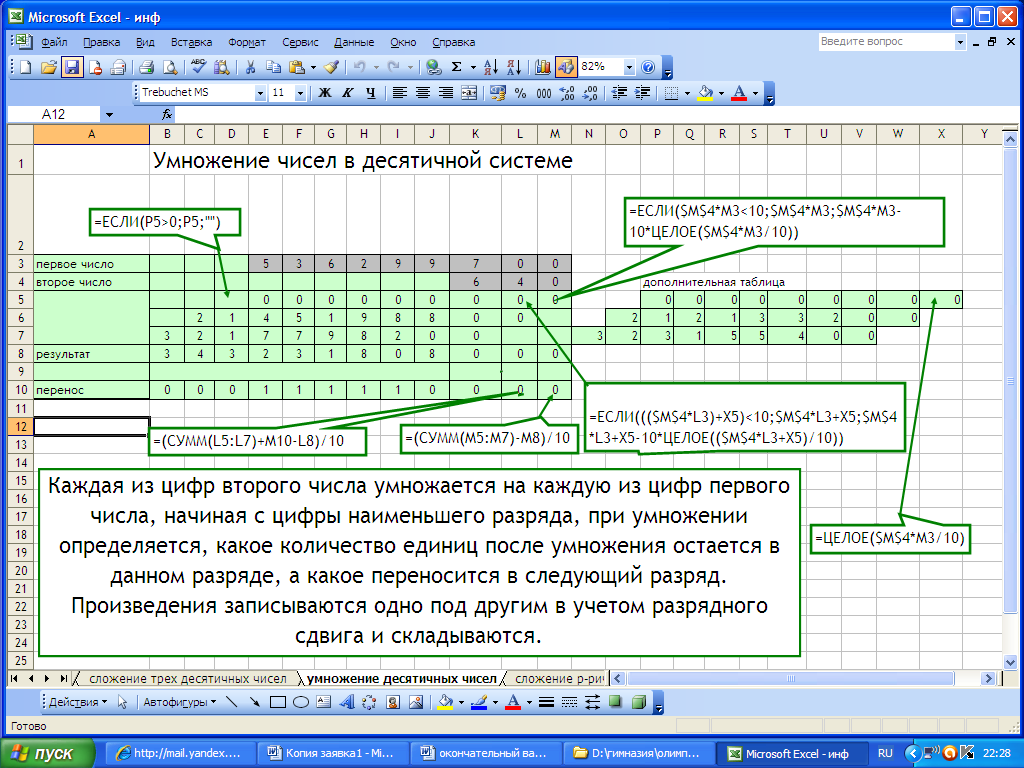
Сформулируем алгоритм поразрядного умножения чисел:

Каждая из цифр второго числа умножается на каждую из цифр первого числа, начиная с цифры наименьшего разряда, при умножении определяется, какое количество единиц после умножения остается в данном разряде, а какое переносится в следующий разряд. Произведения записываются одно под другим в учетом разрядного сдвига и складываются.

1. Пусть первое число девятиразрядное, а второе – трехразрядное.

2. Последовательно умножается цифра наименьшего разряда второго числа на цифры первого числа

=ЕСЛИ($M$4*M3

Для запоминания количества единиц, переносимых в следующий разряд заводим дополнительную таблицу, куда и вносим данные

=ЦЕЛОЕ($M$4*M3/10)

Для подсчета произведения цифры наименьшего разряда второго числа на цифру следующего разряда первого числа формула видоизменяется

=ЕСЛИ($M$4*L3+X5

Изменяется и формула подсчета количества единиц, переносимых в следующий разряд

=ЦЕЛОЕ(($M$4*L3+X5)/10)

Формулы копируются

Проверяют, не появился ли новый разряд. Для этого

Вносим формулу =ЕСЛИ(P50;P5;"")

Производим умножение 2 цифры 2 числа на цифры первого числа

=ЕСЛИ($L$4*M3

=ЦЕЛОЕ($L$4*M3/10)

=ЕСЛИ($L$4*L3+W6

=ЦЕЛОЕ(($L$4*L3+W6)/10)

Формулы копируются

Проверяют, не появился ли новый разряд. Для этого

=ЕСЛИ(O60;O6;"")

Производится умножение цифры старшего разряда второго числа на цифры первого числа.

Затем производится сложение трех полученных чисел.

5 эксперимент

Теперь можно приступить к реализации арифметических операций с двумя числами в различных системах счисления. Традиционные системы счисления с основанием Р иначе называют Р-ичными.

На основании предыдущих экспериментов мы можем сделать вывод о влиянии основания системы счисления на перенос единицы в следующий разряд и то, какое количество единиц остается в данном разряде: если складываются цифры двух чисел в системе счисления с основанием р, то для нахождения количества единиц, оставляемых в этом разряде, из полученного числа вычитается р, а в следующий разряд переходит единица.

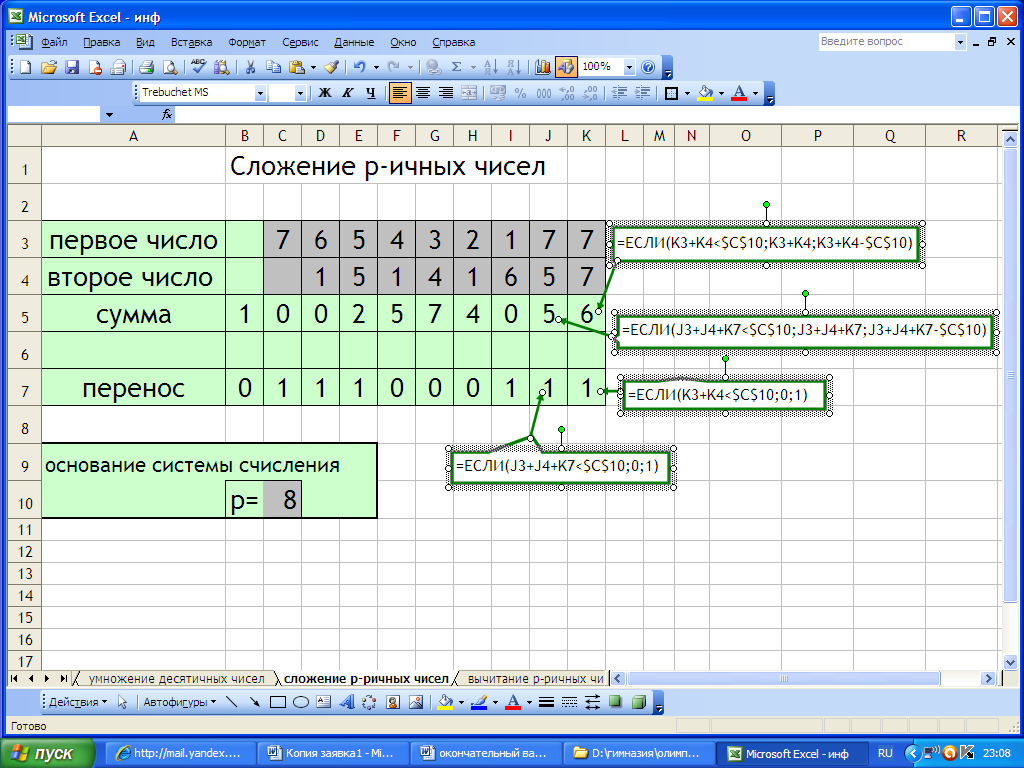
=ЕСЛИ(K3+K4

=ЕСЛИ(J3+J4+K7

=ЕСЛИ(K3+K4

=ЕСЛИ(J3+J4+K7

6 эксперимент

Проведя эксперименты с различными системами счисления, мы заметили, что если используются только две цифры в двоичной системе счисления, то формулы могут быть более простыми.

Так, нет необходимости использовать условные функции, заменив их функцией, реализующей остаток от деления на 2. Аналогичная функция используется в компьютерах и реализуется элементной базой в микросхемах.

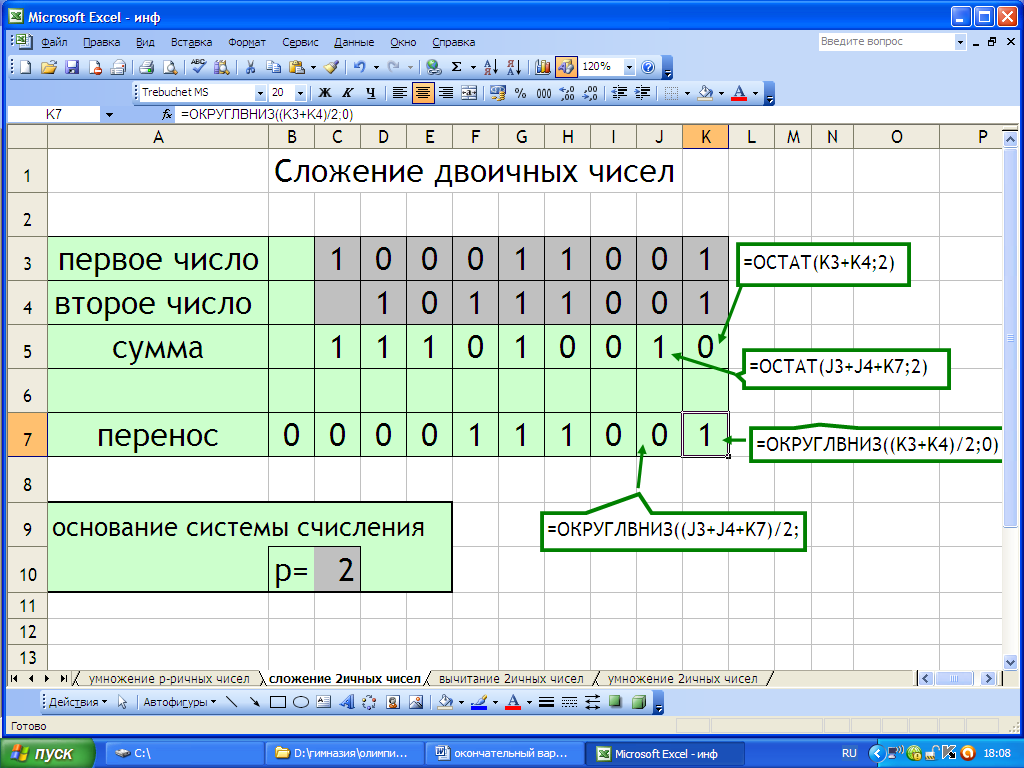
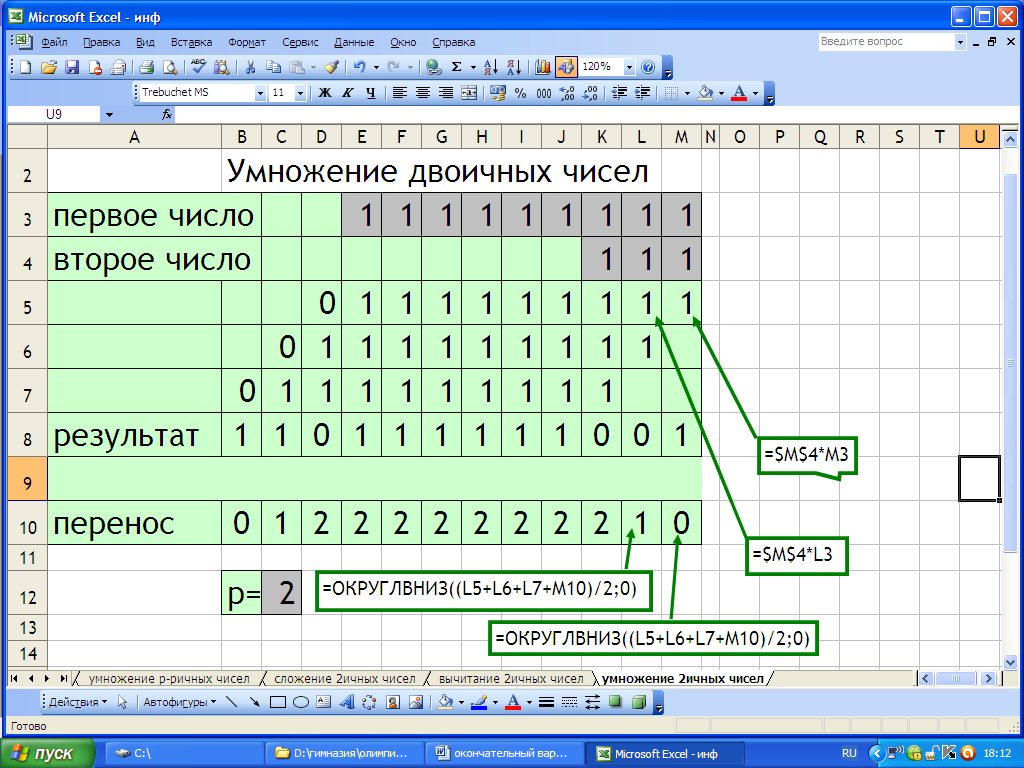
7 эксперимент

Усложним задачу. Будем вводить числа в десятичной системе, переведем их в двоичную систему счисления и запишем поразрядно. Предусмотрим возможность работать с отрицательными числами.

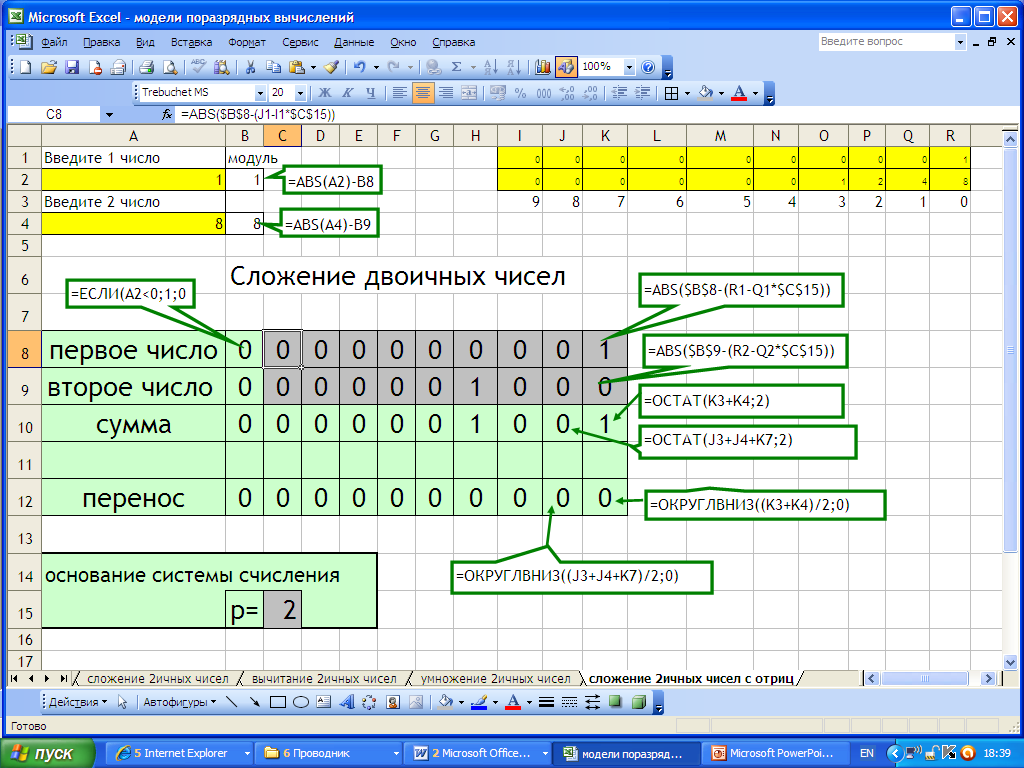
Мы знаем, что отрицательные числа записываются в виде дополнительного кода. Как получить дополнительный код отрицательного числа?
Дополнительный код используется для упрощения выполнения арифметических операций. Если бы вычислительная машина работала с прямыми кодами положительных и отрицательных чисел, то при выполнении арифметических операций следовало бы выполнять ряд дополнительных действий. Например, при сложении нужно было бы проверять знаки обоих операндов и определять знак результата. Если знаки одинаковые, то вычисляется сумма операндов и ей присваивается тот же знак. Если знаки разные, то из большего по абсолютной величине числа вычитается меньшее и результату присваивается знак большего числа. То есть при таком представлении чисел (в виде только прямого кода) операция сложения реализуется через сложный алгоритм. Если же отрицательные числа представлять в виде дополнительного кода, то операция сложения, в том числе и разного знака, сводится к их поразрядному сложению.
Применим следующий алгоритм получения дополнительного кода отрицательного числа.

1. модуль отрицательного числа представим прямым кодом в k двоичных разрядах;

2. значение всех бит инвертировать: все нули заменим на единицы, а единицы на нули (таким образом, получается k-разрядный обратный код исходного числа);

3. к полученному обратному коду прибавим единицу.

Пример:
Получим 8-разрядный дополнительный код числа -52:

00110100 - число |-52|=52 в прямом коде

11001011 - число -52 в обратном коде

11001100 - число -52 в дополнительном коде

Мы поняли, почему обрабатываемую компьютером информацию необходимо преобразовывать именно в двоичный код.

Это связано с возможностью создания электронного элемента, который может устойчиво находиться в одном из двух состояний: намагничено – не намагничено, есть ток – нет тока. Эти два устойчивых состояния и кодируются 1 и 0. Как и любая модель, наша программа ограничена по возможностям. Она работает только системами счисления, не превышающими 10. Однако проводя эксперименты, мы подтвердили вывод о преимуществе двоичной системы счисления.

Выводы:

В ЭВМ используют двоичную систему, потому что она имеет ряд преимуществ перед другими системами:

1.      Для ее реализации нужны технические элементы с двумя возможными состояниями (есть ток, нет тока; включено, выключено и т.д. Одному из состояний ставится в соответствие 1, другому – 0), а не десять, как в десятичной системе.

2.      Представление информации посредством только двух состояний надежно и помехоустойчиво.

3.      Возможно применение аппарата булевой алгебры для выполнения логических преобразований информации.

4.      Двоичная арифметика намного проще десятичной.

5.      Двоичные таблицы сложения и умножения предельно просты.

Литература

1. «Математические основы информатики», Е.В. Андреева, Л.Л. Босова, И.Н. Фалина, Москва, Бином, Лаборатория знаний, 2005

2. «Роль систем счисления в истории компьютеров». А. Стахов, ИЗДАТЕЛЬСТВО "МИР" , Москва, 1989 

3. Информатика: 7-9 класс: Базовый курс: Практикум-задачник по моделированию (под ред. Макаровой Н.В.), Питер,2008

4. Материалы с сайта http://www.computer-museum.ru/