Машина Тьюринга

Подготовил: Яхин Шамиль ,

Ученик 10 «Б» класса МАОУ «МБЛ».

Руководитель: Колотова И.В.

Машина

Тьюринга

Кто такой Алан Тьюринг?

ТЬЮРИНГ (Turing) Алан Матисон (23 июня 1912, Лондон — 7 июня 1954, Уилмслоу, Великобритания), английский математик. Основные труды по математической логике, вычислительной математике. Ввел математическое понятие абстрактного эквивалента алгоритма, или вычислимой функции, получившее затем название «машины Тьюринга».

Теоремы К.Геделя

«Не существует полной формальной теории, где были бы доказуемы все истинные теоремы математики.»

Он показал, что любая математическая теория является неполной, поскольку должны существовать теоремы, истинность которых не может быть доказана в пределах данной теории.

Работа А.Тюринга «О вычислимых числах» (1936)

• Тьюринг доказал, что не существует такого универсального метода для определения вычислимости, и, следовательно, в математике всегда будут задачи, не имеющие решения (в отличие от пока неразрешимых).
• Работа Тьюринга опровергла мнение Д. Гилберта и его школы о том, что любая математическая теория может быть выражена через набор аксиом и теорем.

Что такое машина Тьюринга?

• Это устройство, состоявшее из бесконечной бумажной ленты с записанными на ней символами и считывающей головки, могло решать любые математические или логические задачи.

Жизненный путь Алана Тьюринга

• Во время Второй мировой войны ученый служил в правительственной шифровальной школе в Блетчли, где с помощью первых вычислительных машин пытались расшифровать германские послания, закодированные шифровальной машиной «Энигма».
• В конце 1943 при участии Тьюринга была построена первая вычислительная машина, использовавшая вместо электромеханических реле 2 тыс электронных вакуумных ламп, — «Колосс».

Машина Тьюринга Алгоритмическая система Тьюринга.

Даны два целых положительных числа в различных системах счисления, например одно число – в троичной системе счисления, а другое – в восьмеричной. Необходимо отыскать алгоритм вычисления суммы этих чисел. При этом сумма чисел должна быть записана в любой, наперед заданной системе счисления.

А={0, 1, 2, 3, 4, 5, 6, 7, +, - }.

• Справа – число троичной системы счисления, слева – число восьмеричной.
• От числа, расположенного справа, отнимем единицу, затем продвигаемся влево и к восьмеричному числу прибавляем единицу. После этого возвращаемся к правому числу и повторяем первый цикл. Работа будет продолжаться до тех пор, пока число, расположенное справа, не будет исчерпано. После того как к левому числу прибавляем единицу, в последний раз мы сдвигаемся вправо, стираем знак «+» и останавливаемся.
• Сконструированная машина может выступать и в роли троично-восьмеричного дешифратора.

q 4 1q 4 1q 4 4 0  q 5   5 1q 4 1q 4   q 6   6 1q 4   1q 4     1q 4     1q 4 1q 4 2q 4 7 -q 5 1q 4   1q 4 3q 4 +     1q 4 1q 4 -q 5   - 4q 4   1q 4 5q 4     1q 4 +6q 4       1q 4 1q 4 7q 4     -  0  +q 4 " width="640"

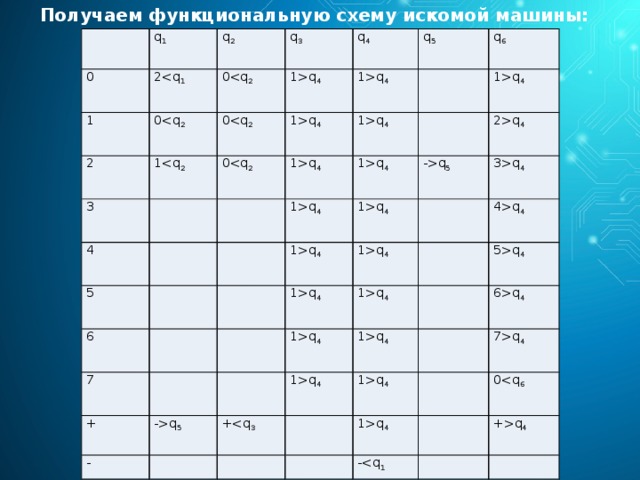
Получаем функциональную схему искомой машины:

q 1

0

1

2

q 2

2

0

0

q 3

1

0

q 4

3

1q 4

1q 4

1q 4

4

0

q 5

5

1q 4

1q 4

q 6

6

1q 4

1q 4

1q 4

1q 4

1q 4

2q 4

7

-q 5

1q 4

1q 4

3q 4

+

1q 4

1q 4

-q 5

-

4q 4

1q 4

5q 4

1q 4

+

6q 4

1q 4

1q 4

7q 4

-

0

+q 4

• Сконструированная машина может выступать и в роли троично-восьмеричного дешифратора

• turing.exe

Проверим, сходится ли результат работы нашей программы с ответом на поставленную задачу.

• 1435 8  = 1∙8 3 +4∙8 2 +3∙8 1 +5∙8 0  = 512+256+24+5 = 797 10

Результат перевода: 1435 8  = 797 10

• 212 3  = 2∙3 2 +1∙3 1 +2∙3 0  = 18+3+2 = 23 10 Результат перевода: 212 3  = 23 10
• 797 10 +23 10  = 820 10

• Окончательный ответ: 1464 8

В результате работы нашей программы получился такой же ответ.

Заключение

Для того, чтобы составить программу для решения конкретной задачи, сначала строят блок-схему алгоритма решения. Затем уже пишут программу, разделяя её на отдельные процедуры в соответствии с блок-схемой. Предложенный гениальным английским математиком Аланом Тьюрингом метод изучения алгоритмов предлагает ещё один способ записи алгоритма, наглядно иллюстрирующий решение конкретной задачи с помощью построения схемы машины Тьюринга. Хотя Тьюринг имел в виду некую идеальную машину, описывая только те её свойства, которые необходимы программисту, в 70-е годы прошлого века в нашей стране были созданы действующие модели машин Тьюринга. Опыт по применению этих моделей в изучении алгоритмов и программирования оказался очень интересным.

Список литературы:

• «Большая энциклопедия Кирилла и Мефодия 2006 »
• В.Н.Касаткин. Информация. Алгоритмы. ЭВМ. М., Просвещение, 1991 г.
• http://lib.custis.ru/index.php/Машина_Тьюринга