Квантовые постулаты Бора. Опыты Франка и Герца.

Физика атома, атомного ядра и элементарных частиц

02. (0). Квантовые постулаты Бора. Опыты Франка и Герца.

Итак, с одной стороны, результаты опытов Резерфорда показывает справедливость планетарной модели атома и не допуска-ют никакой иной интерпретации. С другой стороны, планетарная модель противоре-чит законам классической электродинами-ки. Из этого противоречия может быть сде-лан только один вывод: построить модель атома в рамках классической физики невозможно.

При описании внутриатомных явлений мно-гие законы классической физики неприме-нимы или ограниченно применимы. В мик-ромире действуют представления и зако-ны, описываемые квантовой физикой.

Первой теорией, позволившей правильно описать многие важные свойства атомов, была теория Бора ( Bohr N., 1913г). Благодаря своей простоте и наглядности эта теория до сих пор используется для описания многих внутриатомных явлений.

В основе теории Бора лежат два постулата Бора:

Первый постулат. Из бесконечного числа элект-ронных орбит, возможных с точки зрения клас-сической физики, в действительности осущест-вимы только некоторые определенные орбиты, на которых электрон, несмотря на движение с ускорением, вопреки классической электроди-намике не излучает энергию. На этих орбитах (или в этих состояниях) атомные системы обла-дают энергиями, образующими дискретный ряд : E 1 , E 2 ,… , E n . Все эти орбиты (или состояния) наз. стационарными . Та из стационарных ор-бит, на которой энергия минимальна, называет-ся основной , остальные - возбужденными .

Правило квантования Бора

На вопрос о том, как выделить эти стационарные орбиты из бесконечного множества орбит, разрешаемых класси-ческой механикой, отвечает правило квантования Бора: в стационарном состоянии электрон, двигаясь по круго-вой орбите, должен иметь дискретные квантованные значения момента импульса L :

(2.1)

где n - целое число (квантовое число n = 1, 2, 3, …),

- "приведенная" постоянная Планка

( h - "обычная" постоянная Планка),

m e - масса электрона, v - скорость электрона,

r n - радиус стационарной орбиты,

соответствующей квантовому числу n .

Правило частот Бора

• Второй постулат (правило частот Бора): при переходе электрона с одной стационарной ор-биты с квантовым числом n на другую стацио-нарную орбиту с квантовым числом m излучает-ся (поглощается) один фотон с энергией:

(2.2)

Здесь  - частота излучения, h - "обычная" посто-янная Планка (Planck M.) , E n и E m - энергии электрона на n -й и m -й стационарных орбитах.

Опыты Франка и Герца.

• Непосредственное экспериментальное подтверждение квантовых постулатов Бора было получено в опытах Франка и Герца ( Franck J., Hertz G., 1913 г.). Идея этих опытов заключалась в следующем : атомы разреженного газа “ обстрелива - ются ” электронами, и при этом регист - рируется характер соударения : упругое или неупругое.

eU 2 . " width="640"

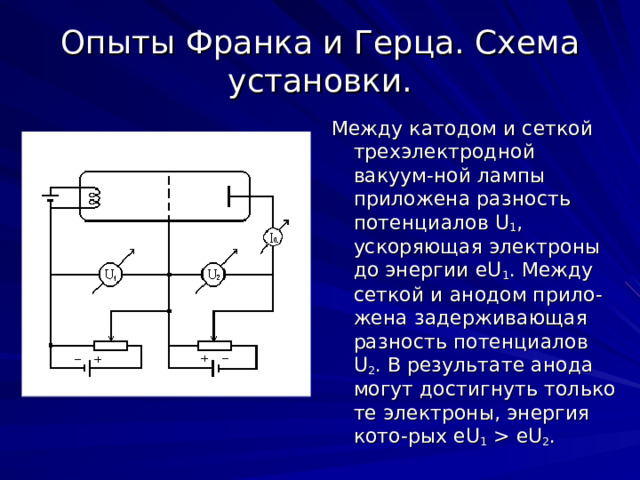
Опыты Франка и Герца. Схема установки.

Между катодом и сеткой трехэлектродной вакуум-ной лампы приложена разность потенциалов U 1 , ускоряющая электроны до энергии eU 1 . Между сеткой и анодом прило-жена задерживающая разность потенциалов U 2 . В результате анода могут достигнуть только те электроны, энергия кото-рых eU 1 eU 2 .

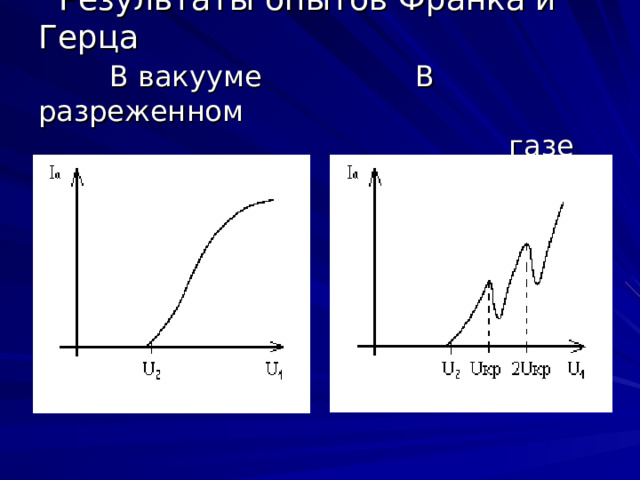
Результаты опытов Франка и Герца В вакууме В разреженном газе

Обобщенная формула Бальмера (Balmer J.)

(2.3)

где R = 109677,6 см -1 - постоянная Ридберга ( Rydberg J. ) .

Формулу Бальмера можно записать в другом виде:

(2.4)

где T(n)=R/n 2 , T(m)=R/m 2 - спектральные термы.

Другими словами, волновое число любой линии спектра водорода можно представить как раз-ность двух спектральных термов.

Комбинационный принцип

Волновое число любой линии спектра других эле-ментов также можно представить в виде разности термов, но при этом термы будут выражаться бо-лее сложными формулами. Например, спектраль-ные термы щелочных металлов можно предста-вить в виде

(2.5)

где  - некоторая эмпирическая поправка. Тот факт, что волновое число любой спектральной линии любого элемента можно представить в виде раз-ности спектральных термов, называется комби-национным принципом Ритца (Ritz W. , 1908г) .

Комбинационный принцип и второй постулат Бора

Если в условии частот Бора обе части равенства разделить на hc :

(2.6)

и обозначить E n /hc = T(n) , E m /hc = T(m) , то мы полу-чим формулу, совпадающую с комбинационным принципом:

(2.7)

Итак, второй постулат Бора - это комбинационный принцип, выраженный другим способом.