ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ
ИНСТИТУТ ИМЕНИ М.Е.ЕВСЕВЬЕВА»
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
КАФЕДРА ИНФОРМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
КУРСОВАЯ РАБОТА
По информатике
Исследование возможностей библиотеки пакетов системы Maxima для решения специальных математических задач
Автор курсовой работы: Жарко Д. Д., студент IV курса группы МДИ-110 очной формы обучения.
Специальность: 050202 «Информатика» с дополнительной специальностью 050201.65 «Математика»
Руководитель: Т. В. Кормилицына, канд. физ.-мат. наук, доцент
Саранск 2014
Содержание
Введение…………………………………………………………………………...3
1 Назначение и возможности пакетов расширений системы Maxima……………………………………………………………………………..5
1.1 Исторические сведения о системе Maxima…………………………….5
1.2 Структура систем символьной математики и назначение пакетов расширений………………………………………………………………………..6
2 Исследование возможностей библиотеки пакетов системы Maxima для решения специальных математических задач…………………………………......................................................................8
2.1 Пакет расширений для моделирования фракталов и алгоритмы решения задач……………………………………………………………………..8
2.2 Пакеты расширения визуализации решений математических задач и алгоритмы решения задач……………………………………………………….16
2.3 Пакеты расширения для решения задач математической статистики и алгоритмы решения задач…………………………………………………….…17
Заключение……………………………………………………………………….21
Список использованных источников…………………………………………...23
Приложение………………………………………………………………………24
Введение
Система Maxima принадлежит классу систем символьной математики. Системы этого класса позволяют проводить аналитические (символьные) вычисления, основанные на рациональной арифметике.
Maxima – система для работы с символьными и численными выражениями, включающая дифференцирование, интегрирование, разложение в ряд, преобразование Лапласа, обыкновенные дифференциальные уравнения, системы линейных уравнений, многочлены, множества, списки, векторы, матрицы и тензоры. Maxima производит численные расчеты высокой точности, используя точные дроби, целые числа и числа с плавающей точкой произвольной точности. Система позволяет строить графики функций и статистических данных в двух и трех измерениях.
Исходный код Maxima может компилироваться на многих системах, включая Windows, Linux и MacOS X. На SourceForge доступны исходные коды и исполняемые файлы для Windows и Linux.
Maxima – потомок Macsyma, легендарной системы компьютерной алгебры, разработанной в начале 60-х в MIT. Это единственная основанная на Macsyma система, все еще публично доступная и имеющая активное сообщество пользователей благодаря своей открытости. Macsyma произвела в свое время переворот в компьютерной алгебре и оказала влияние на многие другие системы, в числе которых Maple и Mathematica.
Работу над Maxima вел Уильям Шелтер с 1982 года и до своей кончины в 2001 году. В 1998 году он получил разрешение на публикацию исходного кода под лицензией GPL. Выживание Maxima стало возможным только благодаря его усилиям и способностям, мы очень благодарны ему за уделенные проекту время и знания эксперта, которые поддерживали код DOE Macsyma актуальным и качественным. После его кончины была сформирована группа пользователей и разработчиков, ставящая своей целью донести Maxima до широкой аудитории.
Актуальность исследования: – в работе исследуются ресурсы Maxima? реализованные в виде встроенных пакетов. В настоящее время пользователями активно изучается возможности данных пакетов, позволяющие использовать мощные дополнительные ресурсы системы, предназначенные для решения специфических задач. Отсутствие учебной литературы является значительным затруднением для обычных пользователей, поэтому описание этих возможностей является актуальным.
Целью данной работы является рассмотрение дополнительных подгружаемых пакетов для системы Maxima, их основных свойств, функций и особенностей, используемых для решения математических задач.
Объект исследования – система компьютерной математики Maxima.
Предмет исследования – возможности пакетов расширений системы Maxima для решения математических задач.
Задачи исследования:
1) исследование библиотеки пакетов расширений и составление каталога пакетов;
2) анализ пакетов расширений, предназначенных для решения математических задач;
3) проведение вычислительных экспериментов с эталонными алгоритмами пакетов расширений;
4) составление алгоритмов решений математических задач в пакетах расширений (фракталы, математическая статистика, графика и визуализация).
Методы исследования:
анализ учебной и научной литературы, источников Интернет;
изучение документации к системе Maxima;
проведение компьютерных экспериментов;
обобщение результатов.
1 Назначение и возможности пакетов расширений системы Maxima
1.1 Исторические сведения о системе Maxima
История проекта, известного сейчас под именем Maxima, началась в конце 60-х в Массачусетском технологическом институте, где в рамках проекта MAC была создана программа символьных вычислений, получившая название Macsyma (MAC Symbolic MAnipulation). Языком программирования был выбран Lisp. Как показало время, это был полностью оправданный выбор, поскольку и сейчас этот язык не только существует, но и продолжает развиваться.
Macsyma была первой программой символьных вычислений, и много положений ее идеологии были позже заимствованы известными сейчас коммерческими продуктами Maple и Mathematica. Macsyma была закрытым коммерческим проектом, поскольку его финансировали, в частности, и военные организации, например, Оборонный и энергетический департамент США (Departments of Energy & Defence, DOE & DOD), Агентство перспективных разработок министерства обороны США (DAPRA - Defense Advanced Research Project Agency), на средства которого, кстати, была создана первая сеть национального масштаба ARPANET. Проект с переменной активностью действовал достаточно длительное время.
В 1982 г. профессор Уильям Шелтер на основе кода Macsyma начал создавать собственную версию программы под названием Maxima. В 1998 г. Шелтеру удалось получить от DOE & DOD права на публикацию кода по лицензии GPL. С этого момента Maxima позиционируется как свободное программное обеспечение с открытым кодом. Сам проект Macsyma прекратил свое существование в 1999 г., но У. Шелтер продолжал заниматься разработкой Maxima вплоть до своей смерти в 2001 г. И после его смерти программа продолжает активно развиваться [1].
Инсталляция Maxima содержит два варианта: консольный (XMaxima) и с графическим интерфейсом (wmMaxima). Система имеет много локализаций, в том числе и русскую. При этом во время инсталляции автоматически выбирается та локализация, языковая раскладка которой по умолчанию является основной. Вместе с тем следует заметить, что русская локализация последних версий является достаточно несовершенной, в ней отсутствует перевод очень многих команд и текста в окнах. Остается только надеяться, что вопрос локализации - это вопрос только времени.
Базовая функциональность системы значительно расширяется специализированными пакетами, предназначенными для работы с размерными величинами, дополнительными функциями для работы с матрицами, работы с графами и т. п. Они есть в составе инсталляции системы и для работы с ними пользователю необходимо во время работы просто загрузить нужный пакет [3].
1.2 Структура систем символьной математики и назначение пакетов расширений
Современные универсальные системы имеют следующую типовую структуру:
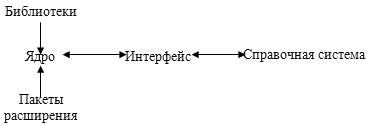
Рисунок 1. – Структура универсальной системы символьной математики.
Центральное место занимает ядро системы. Оно представляет собой множество заранее откомпилированных функций и процедур, представленных в машинных кодах и обеспечивающих набор встроенных функций и операторов системы. Этот набор должен быть функционально полным. Роль ядра особенно велика в системах символьной математики, где в ядре хранятся многие сотни, а то и тысячи правил преобразования математических выражений.
Ядро математических систем тщательно оптимизируется, поскольку от скорости его работы зависит скорость вычислений, выполняемых данной системой компьютерной математики. Этому способствует и предварительная компиляция ядра. Доступ пользователя в ядро с целью его модификации, как правило, исключен. Объем ядра может достигать нескольких мегабайт. Пишется ядро на языке реализации системы – чаще всего это С или С++ (лишь с системе Derive использован язык искусственного интеллекта MuLISP) и компилируется на фирме – разработчике системы.
Интерфейс дает пользователю возможность обращаться к ядру с своими запросам и получать результат решения на экране дисплея. Интерфейс современных систем символьной математики базируется на средствах операционных систем Windows и обладает практически всеми их возможностями: перемещаемые и масштабируемые окна документов, диалоговые и информационные окна, кнопки управления, общение с периферийными устройствами и т.д. Нередко интерфейс систем обеспечивает возможность создания и редактирования библиотечных модулей и пакетов расширения систем.
Функции и процедуры, включенные в ядро, выполняются предельно быстро. С этой точки зрения в ядро было бы выгодно включать как можно больше вычислительных средств. Однако это невольно приводит к замедлению поиска нужных средств из-за возрастания их числа, увеличению времени загрузки ядра и к другим нежелательным последствиям. Поэтому объем ядра ограничивают, но к нему добавляют библиотеки более редких процедур и функций, к которым обращается пользователь, если в ядре не обнаружена нужная процедура или функция. Некоторые системы допускают модернизацию библиотек и их расширение силами самих пользователей [10].
Кардинальное расширение возможностей систем и их адаптация к решаемым конкретными пользователями задачам достигается за счет пакетов расширения систем. Эти пакеты, как правило, пишутся на собственном языке программирования той или иной системы, что делает возможным их подготовку обычными пользователями, хотя в базовую поставку систем включаются профессионально подготовленные фирменные пакеты расширения. Многие фирмы практикуют поставку подобных пакетов, подготовленных многочисленными пользователями таких систем, прежде всего профессионалами-математиками, разумеется, после их тщательной проверки и фильтрации на фирме-разработчике математической системы.
Справочная система обеспечивает получение оперативных справок по вопросам работы с СКМ с примерами такой работы. В справочные системы нередко включают и такой материал, как математические таблицы, формулы для нахождения производных и интегралов, алгебраические преобразования и т. д. Большинство справочных систем написаны на английском языке, что затрудняет их применение нашими пользователями [7].
2 Исследование возможностей библиотеки пакетов системы Maxima
для решения специальных математических задач
2.1 Пакет расширений для моделирования фракталов и алгоритмы решения задач
C помощью пакета fractals автора Jos’e Ram’ırez Labrador можно строить известные фракталы:
– треугольник Серпинского, фракталы. Дерево. Папоротник;
– множество Мандельброта и множества Жюлиа;
– снежинки Коха;
– отображения Пеано: кривые Серпинского и Гильберта.
Данный пакет обладает ограниченными возможностями. Однако рекомендуется изучить его исходный код, находящийся в файле fractals.mac. Параметры всех команд этого пакета, приведённых ниже, можно изменить непосредственно в тексте этого пакета или скопировать соответствующий кусок кода в свою рабочую область и изменить его.
Рассмотрим функции этого пакета.
Команда sierpinskiale(𝑛) – возвращает массив из координат 𝑛 − 1 случайной точки, принадлежащей треугольнику Серпинского, получающемуся рандомизированным алгоритмом.
Функции этой СИФ:
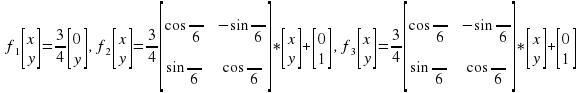
Команда fernfale(𝑛) – возвращает массив из координат 𝑛 − 1 случайной точки, принадлежащей древовидному аттрактору СИФ, получающемуся рандомизированным алгоритмом (здесь вероятности выбора функции зависят от коэффициентов сжатия).
Функции этой СИФ:
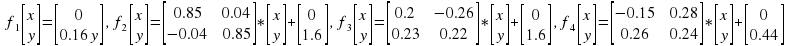
Команда mandelbrot_set(𝑥, 𝑦) – возвращает число 𝑛 ≤ 29 итераций, для которого |𝑓𝑥+𝑦i(𝑛)(0)| ≥ 100, либо число 30, если за 29 итераций орбита точки 0 осталась внутри круга |𝑧| . Напомним, множеству Мандельброта ℳ принадлежат точки 𝑐 = 𝑥 + 𝑦i, для которых орбита нуля ограничена [6].
Эту функцию можно использовать для раскрашивания областей по скоростям убегания точек, например, так:
load(fractals)$
plot3d(mandelbrot_set, [x, -2.5, 1], [y, -1.5, 1.5],
[gnuplot_preamble, "set view map"],[grid, 150, 150])$
Здесь опция grid указывает на то, что область изменения координат [−2.5, 1] ×[−1.5, 1.5] должна быть разделена на 150×150 точек (𝑥, 𝑦), в которых будет вычисляться функция mandelbrot_set(x,y). Опция gnuplot_preamble используется для интерпретации значения функции mandelbrot_set(x,y) как цвета точки (x,y).
Команда julia_set(𝑥, 𝑦) – возвращает число 𝑛 ≤ 29 итераций, для которого |𝑓𝑐(𝑛)(𝑥+𝑦i)| ≥100, либо число 30, если за 29 итераций орбита точки 𝑥 + 𝑦i осталась внутри круга |𝑧| . Здесь число 𝑐 по умолчанию задается переменной julia_parameter:%i. Напомним, заполняющему множеству Жюлиа принадлежат точки 𝑥+𝑦i, орбита которых ограничена. Применять эту команду можно так:
load(fractals)$
plot3d(julia_set, [x, -2, 1], [y, -1.5, 1.5],
[gnuplot_preamble, "set view map"],[grid, 150, 150])$
Автор данного пакета советует опробовать этот код на специальных числах.
Команда julia_parameter: − 0.745 + 0.113002i, −0.39054 − 0.58679i, −0.15652 + 1.03225i, −0.194 +0.6557i, 0.011031 − 0.67037i.
Команда julia_sin(𝑥, 𝑦) – то же, что и предыдущая команда, только для функции 𝑓(𝑧) = 𝑐 sin 𝑧. Автор рекомендует параметр julia_parameter:1+0.1*%i$.
Команда snowmap(𝑣𝑒𝑟𝑡, 𝑖𝑡𝑒𝑟) – возвращает массив вершин снежинки Ко=-21`.ха после 𝑖𝑡𝑒𝑟 итераций, построенной на сторонах ломаной линий, заданной массивом вершин 𝑣𝑒𝑟𝑡 в виде комплексных чисел. Если первая и последняя вершины совпадают, то ломаная линия замкнута. Результирующее множество расположено слева от ломаной линии, считая в направлении от начала к ее концу. Для построения используется рекурсивный алгоритм. Пример использования:
plot2d([discrete,snowmap([1,exp(%i*%pi*2/3),exp(-%i*%pi*2/3),1],4)])$
plot2d([discrete,snowmap([1,exp(-%i*%pi*2/3),exp(%i*%pi*2/3),1],4)])$
Команда hilbertmap(𝑖𝑡𝑒𝑟) – возвращает массив вершин непрерывной кривой Гильберта, плотно заполняющей плоскую область, после 𝑖𝑡𝑒𝑟 итераций.
plot2d([discrete,hilbertmap(4)])$
Команда sierpinskimap(𝑖𝑡𝑒𝑟) – возвращает массив вершин непрерывной кривой Серпинского, плотно заполняющей плоскую область, после 𝑖𝑡𝑒𝑟 итераций.
plot2d([discrete,sierpinskimap(4)])$
Пакет dynamics. load(dynamics)$
C помощью пакета dynamics можно строить различные графически представления динамических систем и фракталов:
– паутинная диаграмма;
– бифуркационная диаграмма;
– эволюция орбиты одно- и двумерного отображений;
– «игра в хаос»;
– система итерированных функций, заданная аффинными преобразованиями;
– множества Жюлиа, Мандельброта;
В нём реализован метод Рунге-Кутты 4-го порядка для решения систем дифференциальных уравнений.
Данный пакет обладает ограниченными возможностями. Однако рекомендуется изучить его исходный код, находящийся в файле «dynamics.mac». Параметры всех команд этого пакета, приведённых ниже, можно изменить непосредственно в тексте этого пакета или скопировать соответствующий кусок кода в свою рабочую область и изменить его [5].
Для вывода графики команды пакета dynamics используют команду plot2d, поэтому все опции 𝑜𝑝𝑡𝑖𝑜𝑛𝑠 этой команды можно передавать в команды пакета dynamics, например, можно менять графические интерфейсы, различные стили графиков, цвета, менять масштаб осей на логарифмический и т.д. Смотрите список опций команды plot2d в справке по Maxima.
Команда chaosgame([[𝑥1,𝑦1],. . .,[𝑥𝑚,𝑦𝑚]],[𝑥0,𝑦0],b,n,options) – реализует «игру в Хаос»: отмечается точка (𝑥0, 𝑦0),
chaosgame([[0,0],[1,0],[0.5,sqrt(3)/2]], [0.1,0.1],1/2,30000,[style,dots])$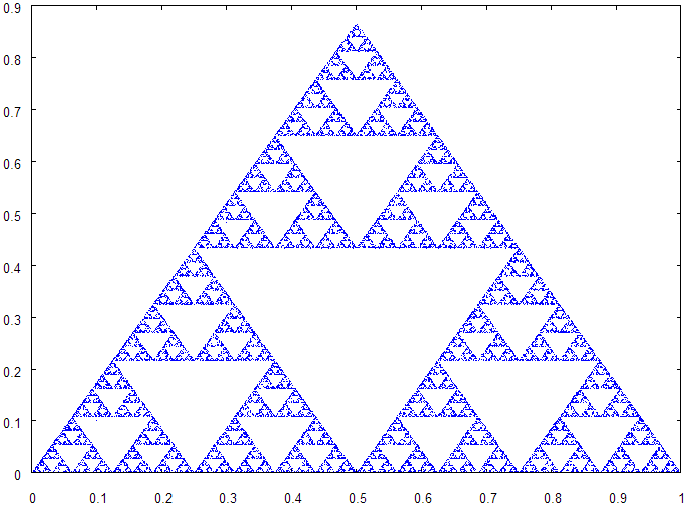
Рисунок 2. – Игра в Хаос.
Команда ifs([𝑟1,...,𝑟𝑚],[𝐴1,...,𝐴𝑚],[[𝑥1,𝑦1],...,[𝑥𝑚,𝑦𝑚]],[𝑥0,𝑦0],n,options) реализует построение аттрактора системы итерированных функций (𝑥0, 𝑦0),
a1:matrix([0.85,0.04],[-0.04,0.85])$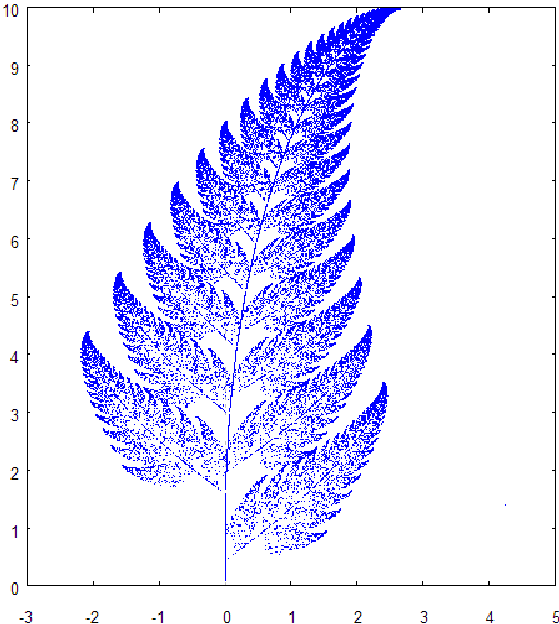
a2:matrix([0.2,-0.26],[0.23,0.22])$
a3:matrix([-0.15,0.28],[0.26,0.24])$
a4:matrix([0,0],[0,0.16])$
p1:[0,1.6]$
p2:[0,1.6]$
p3:[0,0.44]$
p4:[0,0]$
r: [85,92,99,100]$
ifs(r,[a1,a2,a3,a4],[p1,p2,p3,p4],
[5,0],50000,[style,dots])$
Рисунок 3. –Аттрактор системы итерированных функций.
Команда julia(𝑥,𝑦,options) – создаёт изображение множества Жюлиа с параметром 𝑐 =𝑥 + 𝑖𝑦, 𝑥, 𝑦 ∈ R, и сохраняет в файле в формате XPM в директорию установки Maxima [8].
Точки вне множества Жюлиа окрашиваются в различные цвета в зависимости от количества итераций, после которых орбита выходит из круга радиуса 2. Максимальное количество итераций определяется опцией levels. Если после заданного количества итераций орбита точки остается внутри круга радиуса 2, точка окрашивается в цвет, заданный опцией color. Все цвета, в которые раскрашиваются точки вне множества Жюлиа, имеют одинаковую насыщенность (𝑠𝑎𝑡𝑢𝑟𝑎𝑡𝑖𝑜𝑛) и яркость (𝑣𝑎𝑙𝑢𝑒), но разные углы оттенка (ℎ𝑢𝑒), равномерно распределённые между ℎ𝑢𝑒 и ℎ𝑢𝑒 + ℎ𝑢𝑒𝑟𝑎𝑛𝑔𝑒.
Доступные опции, дополнительные к опциям пакета plot2d, опишем в конце секции.
julia(-0.11,0.65569999)$ 
Рисунок 4. – Множество Жюлиа.
Команда mandelbrot(options) создаёт изображение множества Мандельброта и сохраняет в файле в формате XPM. Окрашивание точек происходит по тому же правилу, что и в команде julia.
mandelbrot()$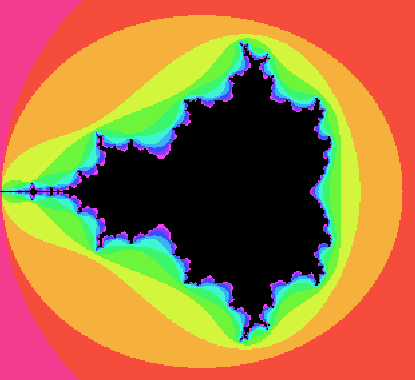
Рисунок 5. – Множество Мандельброта.
Дополнительные опции команд julia и mandelbrot:
– size – задаёт размер изображения в пикселах. При этом size=a (или [size,a])задает квадратное изображение a×a, а [size,a,b]. Если a̸=b, изображение будет выглядеть искаженным. По умолчанию размеры 400×400;
– levels – определяет максимальное число итераций, это число также равно количеству используемых цветов для раскраски точек вне множества. Значение по умолчанию 12. Большие значения требуют большего времени вычислений;
– huerange – задает область углов оттенка (ℎ𝑢𝑒) для раскраски точек вне множества. Значение по умолчанию 360 (это означает, что цвета будут всех оттенков). Если это значение больше 360, область углов оттенка повторяется. Если значение меньше нуля, то углы оттенка будут убывать с количеством итераций;
– hue – задаёт значение оттенка в градусах для первого цвета для окраски точек вне множеств. Значение по умолчанию 300, что отвечает пурпурному цвету (𝑚𝑎𝑔𝑒𝑛𝑡𝑎). Стандартные значения для других цветов: 0 (красный цвет), 45 (оранжевый), 60 (желтый), 120 (зелёный), 180 (голубой, 𝑐𝑦𝑎𝑛), 240 (синий);
– saturation – задаёт насыщенность цвета точек вне множества (в пределах от 0 до1). По умолчанию 0.46;
– value – задаёт яркость цвета точек вне множества (в пределах от 0 до 1). По умолчанию 0.96;
– color – задаёт значение цвета точек множества тремя параметрами: [color,ℎ𝑢𝑒,𝑠𝑡𝑢𝑟𝑎𝑡𝑖𝑜𝑛,𝑣𝑎𝑙𝑢𝑒] (оттенок, насыщенность, яркость). По умолчанию все параметры равны 0, что соответствует чёрному цвету;
– center – задает координаты точки 𝑐 = 𝑥+𝑖𝑦 комплексной плоскости, приходящейся на центр изображения: [center,𝑥,,𝑦]. Значение по умолчанию 𝑥 = 𝑦 = 0 (начало координат находится в середине изображения);
– radius – задаёт радиус наибольшей окружности, умещающейся в изображаемой квадратной области (определяет масштаб изображения). По умолчанию 2;
– filename – задаёт имя файла изображения без расширения. По умолчанию это имя "julia" или "mandelbrot" и файл сохраняется в директорию, в которой установлена Maxima. Если необходимо сохранять файлы в другой директории, следует указать полное имя файла с путём, но без расширения [2].
2.2 Пакеты расширения визуализации решений математических задач и алгоритмы решения задач
Пакет Draw. Загружается пакет с помощью команды load(draw), в который входят:
функция draw2d (опции, explicit (имя_функции, независимая_переменная, min, max), опции) – функция, предназначенная для построения графиков на плоскости с применением большого количества дополнительных опций:
– xrange, yrange – установлены по умолчанию – определяют промежуток изменения значений переменной по осям Ox и Oy. В случае необходимости, можно изменять значений вручную. Например, xrange = [-2, 3];
– grid – в случае, если grid=true, на координатной плоскости выводятся линии сетки;
– title – позволяет выводить заголовок к графику функции. Например, title = "Exponential function";
– xlabel, ylabel – позволяют выводить подписи к осям. Например, ylabel = "Population";
– xtics, ytics – позволяют устанавливать цену деления по осям Ox и Oy, с которой будут наноситься метки на оси. Имеет значение по умолчанию, однако их действием можно управлять вручную. Например, можно задать, чтобы метки по оси Ox наносились на промежутке от -3 до 3 с шагом 0,2: xtics= [ -3, 0.2, 3]. Также можно указать, в каком виде выводить подписи к осям:
– xaxis, yaxis – в случае, если значения этих опций равны true, координатные оси выводятся на экран;
– xaxis_width, yaxis_width – ширина координатных осей (по умолчанию ширина равна 1). Для изменения толщины оси необходимо изменить значение по умолчанию вручную, например, xaxis_width=3;
– xaxis_type, yaxis_type – стиль линии осей Ox и Oy. Допустимые значения: solid и dots;
– xaxis_color, yaxis_color – цвет координатных осей (по умолчанию – черный). Для изменения цвета оси необходимо изменить значение опции вручную, например, xaxis_color = red;
– color – позволяет изменять цвет графика. Например, color=»red» (задается до слова explicit);
– line_width – позволяет изменять толщину линии графика функции (значение по умолчанию – 1);
– line_type – позволяет изменять стиль линии графика функции. Допустимые значения: solid и dots и др.
Заметим, что опции draw могут быть глобальными (тогда в команде draw они стоят после графического объекта) и локальными (тогда их нужно писать перед графическим объектом, поскольку, если таковых несколько, у каждого могут быть свои опции) [1].
2.3 Пакеты расширения для решения задач математической статистики и алгоритмы решения задач
Пакет Maxima включает мощный модуль для линейного и нелинейного оценивания параметров различных моделей с использованием метода наименьших квадратов – пакет lsquares. Основная функция пакета lsquares – это функция lsquares_estimates. Синтаксис вызова:
Lsquares estimates (D,x,e,a) или lsquares estimates (D,x,e,a,initial=L,tol=t)
Функция предназначена для оценки параметров, лучше всего соответствующие уравнению e в переменных x по набору данных D определяются методом методом наименьших квадратов. Функция lsquares_estimates сначала пытается отыскать ищет точное решение, и если это не удаётся, ищет приблизительное решение. Возвращаемое значение – список вида [a = ..., b = ..., c = ...].
Элементы списка обеспечивают минимум среднеквадратичной ошибки. Данные D должны быть матрицей. Каждый ряд - одна запись или один случай, каждый столбец соответствует значениям некоторой переменной. Список переменных x дает название для каждого столбца D (даже для столбцов, которые не входят в анализ). Список параметров содержит названия параметров, для которых отыскиваются оценки. Уравнение e является выражением или уравнением в переменных x и a; если e записано не в форме уравнения, его рассматривают как уравнение e = 0. Если некоторое точное решение может быть найдено при помощи solve, данные D могут содержать и нечисловые значения.
Дополнительные аргументы lsquares_estimates определены как уравнения и передаются дословно функции lbfgs, которая используется, чтобы найти оценки численным методом, когда точный результат не найден. Однако, если никакое точное решение не найдено, у каждого элемента D должно быть числовое значение, в том числе константы (такие как %pi и %e) или числовые литералы (целые числа, rationals, обычные плавания, и bigfloats). Численные расчеты выполнены с обычной арифметикой с плавающей запятой, таким образом все другие виды чисел преобразованы к значениям с плавающей точкой. Для работы с lsquares_estimates необходимо загрузить эту функцию командой load(lsquares) [4].
Пример (точное решение):

Рисунок 6. – Пример решения с помощью lsquares.
Для расчёта невязок для уравнения при подстановке в него данных, содержащихся в матрице, можно использовать функцию lsquares_residuals (D, x, e, a) (смысл параметров тот же, что и для функции lsquares_estimates).
Система Maxima содержит ряд функций для выполнения статистических расчётов (описательной статистики), объединённые в пакет descriptive. Функции, входящие в состав descriptive, позволяют выполнить расчёт дисперсии, среднеквадратичного отклонения, медианы, моды и т.п. Названия функций и краткое описание выполняемых ими действий приведены в таблице [9].
Таблица 1
| Функция | Выполняемые действия | Синтаксис вызова и примечания |
| Mean | Вычисление среднего | mean (list) или mean (matrix) |
| Geometric_mean | Вычисление среднего геометрического | geometric_mean(list) или geometric_mean(matrix) |
| Harmonic_mean | Вычисление среднего гармонического | harmonic_mean(list) или harmonic_mean(matrix) |
| Cor | Вычисляет корреляционную матрицу | cor (matrix) или cor (matrix, logical_value); logical_value равна true или false (false - при расчёте по ковариационной матрице) |
| Cov, cov1 | Вычисляет ковариационную матрицу | cov1 (matrix), cov (matrix) |
| Median | Вычисляет медиану | median (list), median (matrix) |
| Std, std1 | Вычисляет среднеквадратичное отклонение (корень квадратный из var или var1) | аналогично var |
| Var, var1 | Вычисляет дисперсию случайной величины | var1 (matrix), var (matrix), var1 (list), var (list) |
| Central_moment | Вычисляет центральный момент порядка k | central_moment (list, k), central_moment (matrix, k) |
| Noncentral_moment | Вычисляет момент порядка k | noncentral_moment (list, k), noncentral_moment (matrix, k) |
| Skewness | Вычисление асимметрии | Skewness (list), skewness (matrix) |
| Kurtiosis | Вычисление эксцесса | kurtosis(list), kurtosis(matrix) |
| Quantile | Вычисление p-квантиля | quantile (list, p),quantile (matrix, p) |
| Maxi, mini | Выбор наибольшего и наименьшего значения в выборке соответственно | maxi(list), maxi(matrix), mini(list), mini(matrix) |
| Mean_deviation, Median_devation | Сумма абсолютных отклонений от среднего или медианы соответственно | Аналогично mean, median |
| Range | Размах вариации выборки | range (list), range (matrix) |
| List_correlations | Возвращает список, включающий две матрицы - матрицу, обратную ковариационной, и матрицу частных коэффициентов корреляции | list_correlations (matrix), list_correlations (matrix, logical_value)logical_value равна true или false (false - при расчёте по ковари- ационной матрице) |
| Subsample | Аналог функции submatrix |
|
| Global_variances | возвращает список, содержащий различные виды дисперсии | global_variances (matrix) |
Заключение
Целью данной работы являлось рассмотрение дополнительных подгружаемых пакетов системы Maxima. В процессе исследования были использованы следующие методы: синтез, анализ, классификация, сравнение и обобщение.
В работе были реализованы следующие задачи:
Исследованы библиотеки пакетов расширений и составлен каталог из 34 пакетов.
Проведён анализ 5 – и пакетов.
Для выявления возможности пакетов проведены эксперименты для пакетов lsquares и descriptive.
Изучены специальные функции и составлены алгоритмы решения задач:
В ходе изучения материалов по выбранной теме были отобраны 5 пакетов для подробного рассмотрения. C помощью пакета fractals можно строить некоторые фракталы: треугольник Серпинского, фракталы, дерево, папоротник, множество Мандельброта и множества Жюлиа, снежинки Коха, отображения Пеано: кривые Серпинского и гильберта. C помощью пакета dynamics можно строить различные графически представления динамических систем и фракталов: паутинная диаграмма, бифуркационная диаграмма, эволюция орбиты одно – и двумерного отображений, «игра в хаос», система итерированных функций, заданная аффинными преобразованиями, множества Жюлиа, Мандельброта.
В нём реализован метод Рунге-Кутты 4-го порядка для решения систем дифференциальных уравнений. Пакет draw очень распространён так, как является основным пакетом реализации графики в Maxima. Пакет Isquares – это мощный модуль для линейного и нелинейного оценивания параметров различных моделей с использованием метода наименьших квадратов. Пакет Descriptive содержит ряд возможностей для выполнения статистических расчётов (описательной статистики). Функции, входящие в состав descriptive, позволяют выполнить расчёт дисперсии, среднеквадратичного отклонения, медианы, моды и т. п. В Приложении приведён полный список пакетов с кратким описанием их функций.
Данная работа имеет актуальную практическую ценность и может быть использована для углубленного изучения системы Maxima.
Список использованных источников
1. Губина, Т. Н. Решение дифференциальных уравнений в системе компьютерной математики Maxima: учебное пособие / Т. Н. Губина, Е. В. Андропова – Елец : ЕГУ им. И. А. Бунина, 2009. – 99 с.
2. Документация по текущей версии пакета [Электронный ресурс]. – Режим доступа: http://maxima.sourceforge.net/docs/manual/en/maxima_51. html#SEC257.
3. Компьютерная математика с Maxima – Вики-портал образовательных ресурсов Волгоградского государственного социально-педагогического университета [Электронный ресурс]. – Режим доступа: http://wiki.vspu.ru/users/danisrad/maxima/index.
4. Лабораторный практикум «Основы работы в математическом пакете wxMaxima» [Электронный ресурс]. – Режим доступа: http://pedgazeta.ru/pages/ 2012/05/11/end_1336725923.pdf
5. Математический практикум с применением пакета Maxima [Электронный ресурс]. – Режим доступа: http://www.pmtf.msiu.ru/chair31/ students/spichkov/maxima2.pdf.
6. Система компьютерной алгебры Maxima [Электронный ресурс]. – Режим доступа: http://maxima.sourceforge.net/ru/.
7. Сологаев В. И. Maxima: руководство [Электронный ресурс]. – Режим доступа: http://sologaev2010.narod.ru
8. Статьи Тихона Тарнавского [Электронный ресурс]. – Режим доступа: http://maxima.sourceforge.net/ru/
9. Стахин, Н. А. Основы работы с системой аналитических (символьных) вычислений Maxima / Н. А. Стахин. – М. : 2008. – 86 с.
10. Чичкарёв, Е. А. Компьютерная математика с Maxima / Е. А. Чичкарев. – М.: ALT Linux, 2012. – 384 с.
Приложение
| Наименование пакета | Краткое описание функций пакета |
| Augmented_lagrangian | Минимизация функции нескольких переменных с ограниченным методом неопределённых множителей Лагранжа (используется совмесно с lbfgs) |
| Bode | Построение диаграмм Боде (узкоспециальный пакет) |
| Contrib_ode | Дополнительные функции для аналитического решения обыкновенных дифференциальных уравнений |
| Descriptive | Описательная статистика, оценка параметров распределения (генеральной совокупности) по выборке |
| diag | Пакет для операций с некоторыми видами диагональных матриц |
| Distrib | Пакет, содержащий функции для расчёта различных распределений вероятностей и их параметров (нормальное распределение, распределение Стьюдента и т.п.) |
| Draw | Интерфейс Maxima-Gnuplot. Предназначен для подготовки иллюстраций полирафического качества |
| Dynamics | Различные функции, в т.ч. графические, относящиеся к моделированию динамических систем и фракталов |
| F90 | Экспорт кода Maxima в кон на Фортран90 |
| Ggf | Пакет включает единственную функцию, позволяющую оперировать с производящими функциями последовательностей (узкоспециальный пакет) |
| Graphs | Пакет, включающий функции для работы с графами |
| Grobner | Функции для того, чтобы работать с базисом Грёбнера (Groebner) |
| Impdiff | Вычисление производных неявных функций нескольких переменных |
| Implicit_plot | Графики неявных функций |
| Interpol | Пакет, включающий функции интерполяции (линейной, полиномами Лагранжа, сплайнами) |
| Lapack | Функции пакета LAPACK для решения задач линейной алгебры |
| Lbfgs | Пакет минимизации функций нескольких переменных квазиньютоновским методом (L-BFGS) |
| Lindstedt | Пакет, рассчитанный на интерпретацию некоторых типов начальных условий для ОДУ, описывающих колебания |
| Isquares | Функции для оценки параметров различных зависимостей методом наименьших квадратов |
| makeOrders | Пакет включает одну функцию для операций с полиномами |
| Mnewton | Метод Ньютона для решения систем нелинейных уравнений |
| Numericalio | Чтение и запись файлов (преимущественно с матричными числовыми данными) |
| Opsubst | Пакет содержит одну функцию opsubst, позволяющую выполнять замену в выражениях (по возможностям мало отличается от subst) |
| Orthopoly | Пакет, содержащий функции для операций с ортогональными полиномами (Лежандра, Чебышева и др.) |
| Plotdf | Пакет, позволяющий строить поле направлений для решения автономных систем (интересный, но довольно узкоспециальный пакет) |
| Romberg | Пакет, включающий ряд функций для численного интегрирования |
| Simplex | Пакет, предназначенный для решения задач линейного программирования |
| Solve_rec | Пакет, содержащий функции для упрощения рекуррентных выражений |
| Stats | Пакет, включающий функции для статистической проверки гипотез |
| stirling | Расчёт гамма-функции |
| Sringproc | Пакет, включающий функции для обработки строк |
| Unit | Пакет, включающий функции для операций с единицами измерения |
| zeilberger | Функции для гипергеометрического суммирования |


 Получите свидетельство
Получите свидетельство Вход
Вход


















 Курсовая работа по информатике "Исследование возможностей библиотеки пакетов системы Maxima для решения специальных математических задач" (0.25 MB)
Курсовая работа по информатике "Исследование возможностей библиотеки пакетов системы Maxima для решения специальных математических задач" (0.25 MB)
 0
0 1196
1196 48
48 Нравится
0
Нравится
0


