Получите свидетельство
Вход
« Көрсөткүчтүү теңдемелерди жана
барабарсыздыктарды чыгаруу »
Популярдуу сөз айкашынын автору, белгилүү француз математигинин ысымын чечиңиз: «Мен ойлоном, ошондуктан мен бармын».
Мен ойлоном, ошондуктан мен бармын.
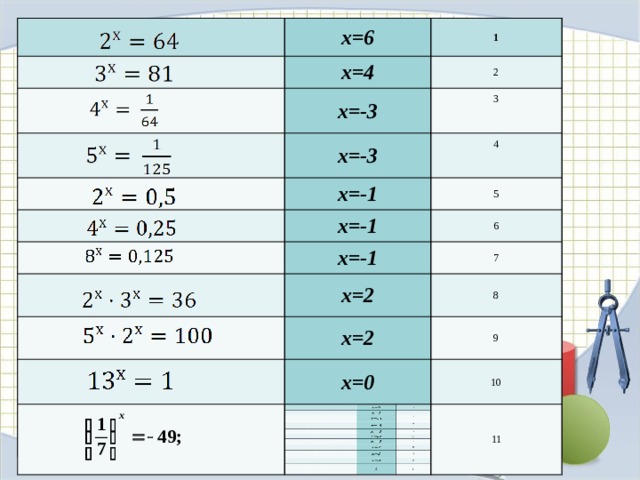
x=6
x=6
x=4
x=4
1
1
x=-3
x=-3
2
2
x=-3
x=-3
3
3
x=-1
4
4
x=-1
x=-1
x=-1
5
5
x=-1
x=-1
6
6
x=2
x=2
7
7
x=2
x=2
8
8
x=0
9
9
x=0
10
10
11
11
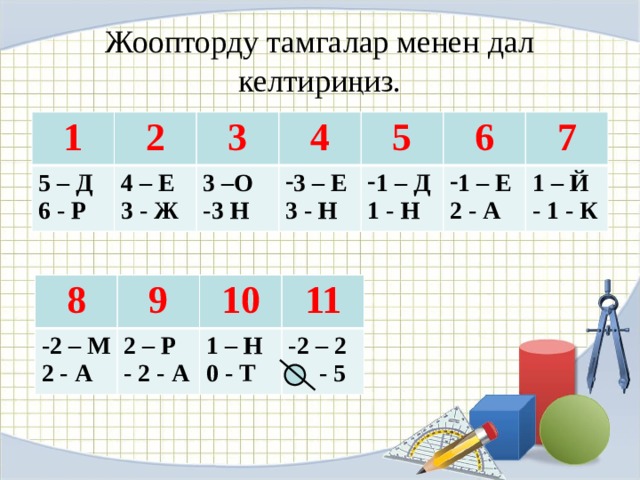
Жоопторду тамгалар менен дал келтириңиз.
1
2
5 – Д
3
6 - Р
4 – Е
4
3 - Ж
3 –О
5
-3 Н
- 3 – Е
6
3 - Н
- 1 – Д
- 1 – Е
1 - Н
7
2 - А
1 – Й
- 1 - К
8
9
-2 – М
10
2 – Р
2 - А
11
1 – Н
- 2 - А
-2 – 2
0 - Т
- 5
Мен ойлоном, ошондуктан мен бармын.
Рене Декарт
- 1 (Д)
6 (Р )
- 1 (Е)
4 ( Е)
- 1 (К )
2 (А)
- 3 ( Н)
2 (Р )
- 3 ( Е )
0 (Т)
(5)
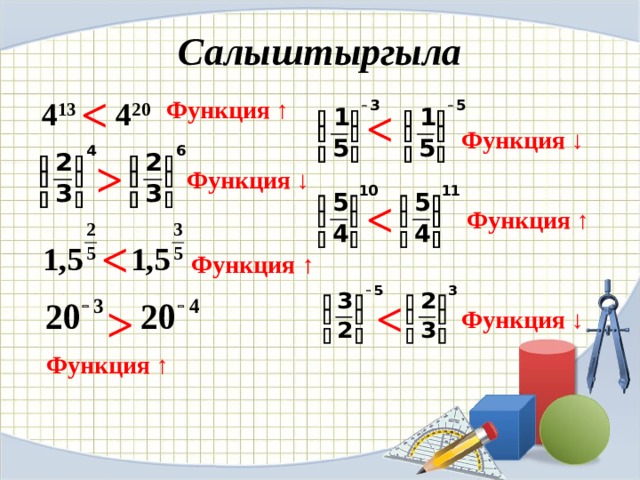
Төмөнкү функциялардын кайсынысы өсүүчү, кайсынысы кемүүчү?
1 " width="640"
Төмөнкү функциялардын кайсынысы өсүүчү, кайсынысы кемүүчү?
Кемүүчү
Өсүүчү
Негизи н өлдөн чо ӊ бирден кичине
0
Негизи бирден чо ӊ
а 1
Функция ↓ Функция ↑ Функция ↑ Функция ↓ Функция ↑ " width="640"
Салыштыргыла
4 13 4 20
Функция ↑
Функция ↓
Функция ↓
Функция ↑
Функция ↑
Функция ↓
Функция ↑
1 болгондо, функция өсөт При а1 функция возрастаетП 0 " width="640"
а 1 болгондо, функция өсөт При а1 функция возрастаетП
0
Көрсөткүчтүү барабарсыздыктар
2
3
1
Аныктама:
Эгерде барабарсыздыкта даражасынын көрсөткүчү өзгөрмө болсо, анда ал көрсөткүчтүү барабарсыздык деп аталат
Мисалы:
0, a 1, b – ар кандай сан " width="640"
Жөнөкөй көрсөткүчтүү барабарсыздыктар
мында a 0, a 1, b – ар кандай сан
Жөнөкөй көрсөткүчтүү барабарсыздыктарды чыгаруу.
Жөнөкөй көрсөткүчтүү барабарсыздыктарды чыгарууда, көрсөткүчтүү функциянын өсүү жана кемүү касиеттери колдонулат
Барабарсыздыктын белгиси
Ѳзг өрөт
Сакталат
Көрсөткүчтүү барабарсыздыктарды чыгаруу жолдору :
- Көрсөткүчтөрдү теңдөө ыкмасы.
- Көбөйтүүчүлөргө ажыратуу.
- Жаңы өзгөрмөнү киргизүү.
Барабарсыздыкты чыгаргыла: 1.Көрсөткүчтөрдү теңдөө ыкмасы .
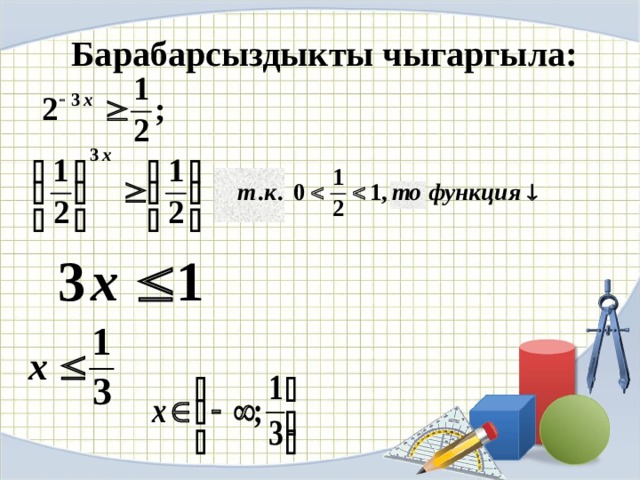
Барабарсыздыкты чыгаргыла:
1, ф-ция ↑ " width="640"
2-ыкма. Көбөйтүүчүлөргө ажыратуу
3 1, ф-ция ↑
1, ф- ция ↑ Жообу: 0 х . " width="640"
3-ыкма. Жаңы өзгөрмөнү киргизүү.
9
1
31, ф- ция ↑
Жообу: 0 х .
Көрсөткүчтүү барабарсыздыктар
2
3
1
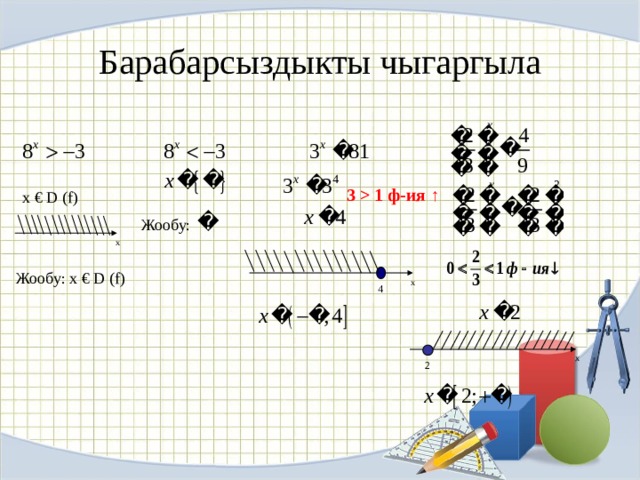1 ф-ия ↑ Жообу: x x 4 x 2 " width="640"
Жообу: х € D (f)
Барабарсыздыкты чыгаргыла
х € D (f)
3 1 ф-ия ↑
Жообу:
x
x
4
x
2
1 ф-ия ↑ Барабарсыздыкты чыгаргыла x -5 -5 " width="640"
5 1 ф-ия ↑
Барабарсыздыкты чыгаргыла
x
-5
-5
1 ф-ия ↑ Барабарсыздыкты чыгаргыла _ х 1 = 2 х 2 = 3 + + 3 2 Ответ: " width="640"
71 ф-ия ↑
Барабарсыздыкты чыгаргыла
_
х 1 = 2 х 2 = 3
+
+
3
2
Ответ:
1 ф-ция ↑ 0 ≤ х ≤ 1 Х € [0;1] Ответ: [0;1] _ + + 3 1 Резерв " width="640"
Барабарсыздыкты чыгаргыла
3 2х – 4 ∙ 3 х + 3 ≤ 0
3 х = y
y² - 4y + 3 ≤ 0
у = 3; 1
1≤ y ≤ 3
1≤ 3 x ≤ 3
3 0 ≤ 3 x ≤ 3
3 1 ф-ция ↑
0 ≤ х ≤ 1
Х € [0;1]
Ответ: [0;1]
_
+
+
3
1
Резерв
Үй тапшырмасы
Рефлексия
1, ф-ия ↑ -1 ≤ х – 3 2 ≤ х " width="640"
- Барабарсыздыкты чыгаргыла:
7 1, ф-ия ↑
-1 ≤ х – 3
2 ≤ х
1, ф-ия ↑ 10х + 15 х Үй иши " width="640"
- Барабарсыздыкты чыгаргыла:
2 1, ф-ия ↑
10х + 15
х
Үй иши
- Барабарсыздыкты чыгаргыла:
0,75 2 + 4х ≥ 0,75 1 – 8х
мында 0
2 + 4х ≤ 1 – 8х
12х ≤ - 1
Бүгүн сабакта
Мен эстедим……..
Мен аткардым………
Мен үйрөндүм ……….
Мен эстеп калдым ……
Мен аткара алам………
Мен ойлоном, ошондуктан мен бармын. Рене Декарт
Сабакка катышканыңарга рахмат !
Көрсөткүчтүү теңдемелерди жана барабарсыздыктарды чыгаруу (841.83 KB)
0
336
11
Нравится
0
