Значение механики в общем школьном физическом образовании.
При обучении механике в общеобразовательной средней школе решаются определенные образовательные, воспитательные задачи развития учащихся.
Образовательные задачи: механика определяется тем что вводят основные понятия (масса, сила, импульс тела, энергия, т.д.) являющимся инструментом познания в физике. В этом смысле механику справедливо считать фундаментом физики. В механике учащиеся знакомятся с физической теорией классической механикой ньютона и такими обобщениями, как закон всемирного тяготения, законы сохранения импульса и энергии, общие условия равновесии механической системы и др.
Воспитательные задачи (формирование научного мировоззрения) решаются путем:
формирование диалектико-материалистического взгляда на природу и её познания.
формирования практических знаний и умений (знание научных основ современной механизации промышленности, транспорта, сельского хозяйства).
раскрытия на уроках физики основных направлений развития и ускорения в современном производстве.
воспитание интернационализма и патриотизма.
трудовое воспитание.
Одной из отличительных особенностей физики, как предмета школьного образования, является необходимость сочетать изучение теоретических положений дисциплины с практическим применением знаний при проведении экспериментов и решении физических задач. При этом разработанные в прошлом классификация школьных физических задач, рекомендации по методике их решения в настоящих условиях требуют определенных коррекций.
Как известно, школьная физика начинается с механики, и это связано с рядом особенностей предмета. Первая особенность этого раздела заключается в том, что именно с механики обычно начинают изучение курса физики в средней школе. Это объясняется тем, что механические процессы являются форма движения, наиболее доступной для наблюдения. К тому же моделирование физических систем в классической физике связано с созданием механических образов. Это определяет место механики в образовательном курсе физики и требует от учителя внимания к прочному усвоению учащимися материала.
Вторая особенность состоит в том, что в механике достаточно полно представлена физическая теория (ни в одном другом разделе школьного курса физики этого нет). В любой физической теории можно условно выделить основание, ядро и вывод.
Основанием механической теории можно считать идеализированный объект - материальная точка; определенное число экспериментальных фактов (опыт Галилея, Кавендиша и др.); основные физические величины: перемещение, скорость, ускорение, масса.
Ядро механической теории включает в себя систему абстракций (постулаты об однородности и изотропности пространства, об однородности времени, о мгновенном воздействии однородного тела на другой без материальных посредников); законы Ньютона, принцип независимости действия сил.
Выводы этой теории включают возможность определения положения материальной точки в пространстве в любой момент времени заданной силе (или равнодействующей силе и начальным условиям).
Состояние механической системы во все последующие времена однозначно вытекает из ее начального состояния и определяются уравнением Ньютона. Взаимодействие осуществляется на расстоянии (минуя материальные носители) и определяется мгновенно (принцип дальнодействия).
Третья особенность раздела - использование эксперимента в преподавании механики. Эксперимент является источником познания.
В программе общеобразовательной школы механика представлена четырьмя подразделами:
В кинематике изучают равномерное и равноускоренное прямолинейное движение, криволинейное движение и их характеристики. Вводят понятия материальной точки, траектории, перемещение и пути пройденного телом вдоль траектории, системы отсчета, скорость и ускорение. При формировании понятий перемещения, скорости, ускорения большое внимание уделяют векторному характеру этих величин. В рамках прямолинейных движения усвоение векторного характера скорости и ускорения затруднено (все векторные направления вдоль одной прямой, и действие над ними можно проводить алгебраически). Завершается раскрытие векторного характера этих величин при рассмотрении криволинейного движения.
В динамике сначала рассматривают первый закон Ньютона, вводят основные динамические характеристики движения - массу и силу. А затем второй закон Ньютона, в котором представлена связь между силой, ускорением и массой. Чтобы записать закон Ньютона для случая действия на тело нескольких сил, рассматривают сложение сил, после этого вводят третий закон Ньютона. Законы Ньютона являются фундаментальными в механике, обобщающими, подтвержденными практикой и экспериментом.
В ходе изучения видов сил в механике (гравитационных, упругих, трения) выявляют зависимость их от взаимного расположения тел и от скорости движения одного тела относительно другого.
После введения гравитационных сил изучают закон всемирного тяготения, дают понятие о силе тяжести и рассматривают движения, в которых изменения происходят в результате действия силы тяжести.
Далее рассматривают силы упругости и закон Гука. Понятие веса тела вводят как пример силы упругости. Завершают рассмотрение видов сил механике изучением силы трения, коэффициента трения и изменение скорости движущегося тела в результате действия силы трения. Показывают, что гравитационные силы и силы упругости являются функцией расстояние между взаимодействующими телами, а силы трения - функцией относительно скорости.
Раздел статика традиционно входит в школьный курс механики, в программе общеобразовательной средней школы, которую мы используем, отсутствует. Однако элементы статики, рассмотренные еще в основной школе, и понятие сложение сил, центра тяжести, включены в программу старших классов, позволяют сформулировать общие условия равновесия.
Группировка материала вокруг законов сохранения импульса и энергии вызвана определяющими значениями законов сохранения современном естествознании. Эти законы связаны со свойствами пространства и времени (закон сохранения энергии – с однородностью времени, закон сохранения импульса – однородностью пространства). Законы сохранения справедливы для импульса и для энергии, в электродинамике и квантовой механике.
Идея относительности проходит красной нитью через весь курс механики: относительность механического движения и покоя, трение, скорость, импульс тела, работа, кинетическая энергия, инвариантность времени, расстояние между взаимодействующими телами, ускорение, масса, сила и др.
При изучении механики показывают, что ёё законы справедливы для инерциальных систем отсчета, что равномерное прямолинейное движение систем отсчета не влияют на механические процессы, то есть по существу раскрывают принцип относительности Галилея.
В школьном курсе механики, изучают механические колебания и волны (особый вид передачи энергии без переноса самого вещества), еще с одним видом механического движения, расширяют представление о периодических процессах.
Например: при изучении движения материальной точки по окружности вводят понятие периода и частоты. При рассмотрении колебаний уточняют эти характеристики и выявляют общее и отличительное для движения материальной точки по окружности механического колебания.
При изучении свободных и вынужденных колебаний выделяют основные признаки этого движения (прямая пропорциональность силы смещению и противоположность направления смещения действующей силы). При рассмотрении уравнений гармонических колебаний понятия фазы не вводят. Программа общеобразовательной средней школы предполагает введение понятия фазы в электродинамике.
Завершают изучение механики рассмотрением механических волн, её основные характеристики и примером механической волны (звук и его характеристики.
Контрольные вопросы и задания по основным разделам школьного курса механики
Представлена систематическая подборка вопросов и заданий по физике, способствующих более глубокому пониманию основных разделов базовой программы для 10 класса, рассчитанной на работу с учебником Мякишева1.
Тематика заданий отражает реальные физические ситуации, знакомые школьникам по их повседневной жизни. Некоторые из заданий сформулировано в немного ироничном стиле; некоторые из них представлены в полу игровой форме, но в основе каждого лежат вполне серьёзные физические закономерности. Предполагалось, что подобный подход будет способствовать развитию интереса школьников к предмету.
Помимо традиционной формы тестовых заданий с вариантами числовых ответов используется открытая форма заданий, когда ученик сам вписывает свою версию ответа в предусмотренное место; заполняет таблицы; находит нужную информацию по графикам и рисункам. Форма «меню» также несколько модифицирована; предлагаемые версии ответа, как правило, не являются абсолютно неверными, а отражают различные подходы к поставленной проблеме, или являются своеобразными подсказками. Уровень сложности заданий варьируется от совсем элементарного (ответ – строчка из учебника), до достаточно высокого, требующего определённых раздумий. В любом случае, материала, изложенного в школьном учебнике (при условии внимательного прочтения) вполне достаточно, чтобы найти ответы на все вопросы.
Ниже описываются некоторые физические процессы и явления, а вам предстоит выбрать, какие из них могут быть описаны в рамках а) классической механики Ньютона, б) специальной теории относительности; в) квантовой механики. Свои варианты ответов занесите в таблицу.
Автомобиль трогается с места, резко набирает скорость и заворачивает за угол.
В линейном ускорителе заряженных частиц протоны разгонялись до скорости, которая всего на 0,1% была меньше скорости света в вакууме.
Источником энергии Солнца и большинства других звезд являются реакции термоядерного синтеза гелия из водорода.
По сообщениям информационных агентств, очередной спутник связи был успешно выведен на околоземную орбиту.
На испытаниях нового стрелкового оружия результаты превзошли самые смелые ожидания.
Конечной стадией цепочки радиоактивных распадов является образование устойчивого изотопа свинца.
| Явление Теория | 1 | 2 | 3 | 4 | 5 | 6 |
| Классическая механика |
|
|
|
|
|
|
| Спец. теория относительности |
|
|
|
|
|
|
| Квантовая механика |
|
|
|
|
|
|
Кинематика Кинематика точки
Можно ли, описывая движение автомобиля, считать его точкой?
Нет, если, конечно, это не детская игрушка, а настоящая машина.
Можно, если смотреть на него с очень большого расстояния.
Нельзя, потому что он состоит из многих частей и деталей.
Можно в тех случаях, когда его размеры значительно меньше расстояний, на которых происходит его движение.
Известно, что положение точки в пространстве можно задать, используя координатный метод, или применяя понятие радиус – вектора. Ниже перечисляются различные ситуации, в которых возникает необходимость определить положение тел в пространстве. А вам предлагается выбрать, какой из методов лучше подходит в каждом конкретном случае.
Свою версию ответа укажите в таблице, поставив крестик или другой знак в нужной клеточке.
Сотрудник ГИБДД, укрывшись за придорожными кустами с радаром в руках, провожал зорким взглядом каждый автомобиль, мчавшийся по прямолинейному участку шоссе.
Бригада специалистов провозилась не менее часа, прежде чем антенна спутниковой связи заняла нужное положение, и на экране телевизора появилось четкое изображение.
Отряд отдыхал, расположившись в тени развесистых деревьев, а руководитель похода с инструктором склонились над картой, оценивая следующий участок маршрута.
Задрав головы вверх и затаив дыхание, зрители наблюдали за фигурами высшего пилотажа, выполняемыми реактивными истребителями.
«Е-2 – е-4» сказал Остап Бендер, и сделал первый ход на очередной шахматной доске.
Кто-то тяжело засопел и заухал в душной темноте ночи прямо над головами ребят, и только когда яркий луч фонарика выхватил нахохлившуюся на ветке птицу, Маша немного успокоилась.
| Ситуация Метод | 1 | 2 | 3 | 4 | 5 | 6 |
| Координатный |
|
|
|
|
|
|
| Радиус - вектор |
|
|
|
|
|
|
| Не подходит ни один метод |
|
|
|
|
|
|
Постарайтесь вспомнить, чем векторные величины отличаются от скалярных величин; приведите примеры тех и других, имеющих отношение к кинематике (в отведенном ниже месте)
Вот если складывать обычные числа, то 3 плюс 4 всегда получается 7. А если складывать векторные величины с модулями 3 и 4 соответственно?
Какая разница, что складывать; математика есть математика, всегда будет получаться одно и то же; в данном случае – 7.
Если будут векторные величины, то их вообще нельзя складывать, потому что у них есть направления.
Это только в геометрии можно складывать векторы по правилу параллелограмма или треугольника.
Может получиться по модулю все, что угодно, в интервале от 1 до 7.
| 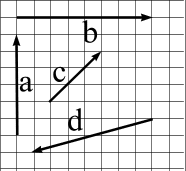 |
| Рис. 3.1 Компания векторов |
На одной математической плоскости жили – были векторы. Их звали
a, b, c и
d. Они были разной длины и смотрели своими стрелками в разные стороны, но это не мешало им дружить и время от времени складываться или вычитаться. (Правда, они еще умели умножаться, но об этом пока вам знать не следует). Внимательно посмотрев на рисунок, ответьте на некоторые вопросы об этих векторах.
Сможете найти в компании векторов на рис. 3.1 самого большого и самого маленького по модулю? За одно уж подсчитайте примерно их длину.
Что больше: сумма векторов a и b, или их разность? Не забудьте пересчитать клеточки!
Конечно, сумма; 6 клеточек у вектора a, 8 – у вектора b; всего получаем 14; разность была бы 2 клеточки.
Этим векторам все равно – складываться, или вычитаться; каждый раз получается одно и то же – 5 клеточек.
В отличие от чисел, векторы надо складывать по методу параллелограмма или треугольника; в клеточках не посчитаешь.
Их вообще нельзя складывать или вычитать, они же в разные стороны направлены!
Если бы векторы, как ни будь, решили сложиться, у них сколько (в клеточках) получилось бы?
Сложить можно только два вектора, а тут их целых четыре; тем более, длина не указана.
Если сложить по всем правилам, получится вектор длиной примерно 7,2 клеточки.
Получаем при сложении 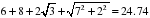 , если, конечно, немного округлить.
, если, конечно, немного округлить.
Их невозможно сложить в таком маленьком квадратике, просто места не хватит.
Первый запуск ракеты на твердом топливе, созданной энтузиастами из школьного кружка, проводился на территории школьного двора, временно используемого в качестве полигона. Испытания прошли удовлетворительно, поскольку все окна остались целы. Компьютерная обработка видеосъемки запуска показана на рис. 3.2
| 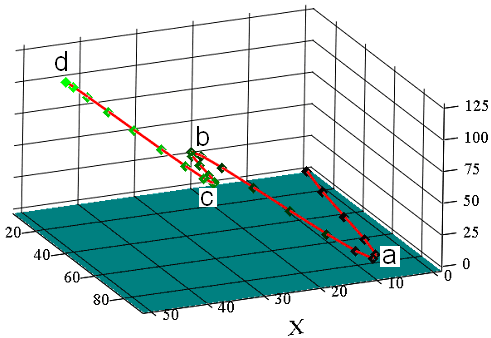 |
| Рис. 3.2 Компьютерная обработка видеозаписи старта ракеты, произведенного на школьном дворе в обстановке особой секретности. Точки в виде квадратиков на траектории показывают положение ракеты через равные промежутки времени. Координаты указаны в дециметрах (чтобы никто не догадался). |
Проанализировав результаты испытаний, комиссия под председательством Пети из 10-Б постаралась ответить на ряд вопросов:
Как назвать (для протокола испытаний) извилистую линию, вдоль которой двигалась ракета после старта?
На какую максимальную высоту поднималась ракета, прежде чем взорваться?
Каковы примерные координаты наиболее характерных точек траектории a, b, c и d?
На последнем участке траектории скорость ракеты увеличивалась, или уменьшалась?
|  |
| Рис. 3.3 Беговая дорожка стадиона |
Беговая дорожка стадиона представляла собой правильную окружность радиусом R = 50 м. Место старта отмечено точкой
а; отмечены также (
б,
в, и
г) некоторые другие характерные точки дорожки (см. рис. 3.3). Считается, что с места старта спортсмены бегут равномерно, хотя скорость у них может быть разная. Место финиша не указано, потому, что на тренировке они бегают, пока не надоест.
С места старта Вася пробежал 2 круга и ещё немного (до точки б), и почти не устал, только надоело бежать, да и девчонки уже ушли.
На сколько метров при этом Вася переместился от старта?
На что была похожа траектория движения спортсмена, пока он не остановился?
Сможете подсчитать его скорость на беговой дорожке, если бежал он всего 2 мин 16 сек? (на всякий случай: длина окружности равна 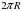 )
)
1. 4 м/с; 2. 4,5 м/с; 3. 5 м/с; 4. 5,5 м/с.
Пока Вася там бегал по дорожке, со скамейки для зрителей (на рисунке она не показана) за ним внимательно следили глаза гражданки М; причем исключительно из познавательных целей:
Можно ли рассматривать Васю как точку, если три раза в неделю он ходит в спортивный зал?
Может ли в процессе движения по окружности перемещение точки в проекции на оси координат быть отрицательным?
На каком участке траектории проекция перемещения на ось х была наибольшей по модулю и отрицательной?
1. а – в 2. б – г 3. г – б 4. в – а
Не часто удается наблюдать НЛО на ясном небе, да еще и снять его с помощью камеры сотового телефона. Изображение, правда, получилось совсем неразборчивое, но координаты объекта в зависимости от времени записать удалось. По этим данным, кстати, построен график движения на рис. 3.4.
| 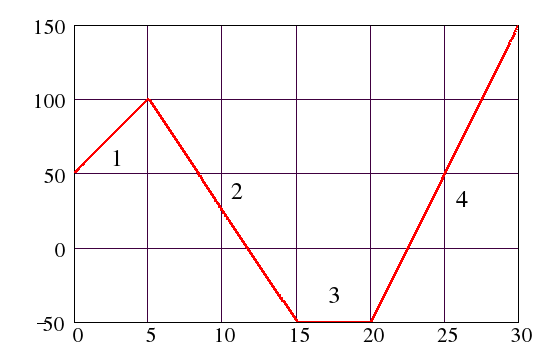 |
| Рис. 3.4 График движения НЛО; по горизонтали – время движения, секунды; по вертикали – координата тела, метры |
Требуется ответить на ряд вопросов, связанных с загадочным движением объекта:
Какой путь прошел объект за время наблюдения?
На сколько метров он при этом переместился от своего начального положения?
Какова была максимальная скорость наблюдаемого объекта?
Какова была его минимальная скорость?
Определите среднюю скорость движения объекта за время наблюдения.
| 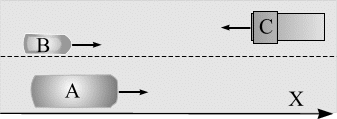 |
| Рис. 3.5 Участок прямолинейного шоссе |
Представьте себе участок прямолинейного ровного шоссе, по которому в обе стороны мчатся автомобили. Проведите мысленно координатную ось Х, чтобы было удобно описывать движение автомобилей. Пусть скорость автобуса (А) 80 км/ч; иномарки (В) 120 км/ч; встречного грузовика (С) 100 км/ч (см. рис 3.5). Выясните, каким должно быть уравнение движения каждого из транспортных средств А, В и С; возможные варианты:
1. 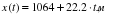 ; 2.
; 2. 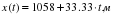
3. 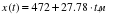 ; 4.
; 4. 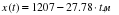
На сколько метров успевает переместиться иномарка за время 10 сек, пока водитель вставлял новый диск в плеер?
1. 303 м; 2. 313 м; 3. 333 м; 4. 363 м.
Какой способ описания движения автомобилей вам кажется более удобным:
Векторный метод, как наиболее универсальный.
Координатный метод, потому что проведена ось х.
Линия, по которой движется точка, называется траекторией.
| 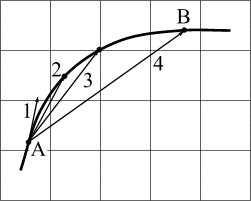 |
| Рис. 3.6 Криволинейный участок дороги. Вид сверху. |
Все способы не пригодны, т. к. не указано тело отсчета.
Рано или поздно, но все хорошее кончается; в том числе, прямолинейный участок дороги. Криволинейных участков бывает больше. Один из них, например, показан на рис.3.6. В какой-то момент времени автомобиль (на рисунке его не видно, это вид с большой высоты) находится в точке А; рано или поздно, он окажется в точке В.
Давайте вспомним определения некоторых физических величин:
Линия, вдоль которой происходит движение точки
Вектор, соединяющий начальное и конечное положение точки
Длина участка траектории от начального до конечного положения точки
Отношение перемещения 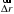 к интервалу времени
к интервалу времени 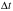 , за которое это перемещение произошло (на криволинейной траектории)
, за которое это перемещение произошло (на криволинейной траектории)
Допустим, пройденный автомобилем путь из точки А в точку В (длина дуги АВ на рис. 3.6) равен 360 м; модуль перемещения из точки А в точку В (хорда АВ) равен тогда 340 м. Время движения 20 сек. Как правильно найти среднюю скорость автомобиля на этом участке?
По формуле из учебника (стр. 20) 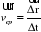 ; тогда модуль средней скорости равен 340/20 = 17 м/с.
; тогда модуль средней скорости равен 340/20 = 17 м/с.
Т. к автомобиль все-таки ехал по дороге, среднюю скорость надо находить по формуле 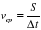 ; т. е. 360/20 = 18 м/с.
; т. е. 360/20 = 18 м/с.
Все зависит от того, ищем мы среднюю скорость перемещения, или путевую среднюю скорость. Тогда и ответ должен получаться разным.
При движении по криволинейной траектории бывает только мгновенная скорость; средняя скорость может быть только на прямолинейной траектории.
Какой вектор из числа показанных на рис. 3.6 дает правильное направление вектора мгновенной скорости в точке А?
Изменится ли направление вектора мгновенной скорости в точке В, если автомобиль движется по дороге равномерно? В любом случае, объясните, почему
На рис. 3.7 показан график скорости тела, движущегося по прямолинейной траектории. Точками на графике отмечены четыре момента времени, для которых измерялась мгновенная скорость тела. Значения скорости известны, только перепуталось, какому моменту времени какая скорость соответствует.
| 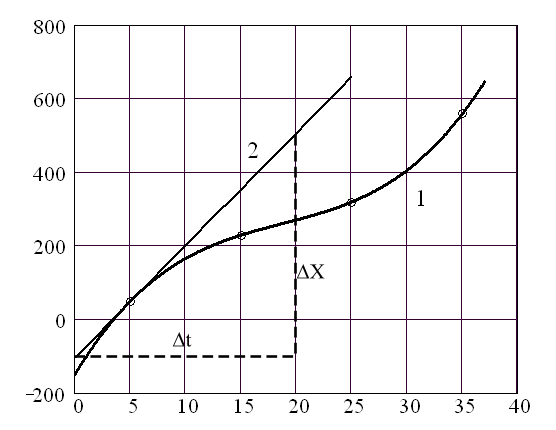 |
| Рис. 3.7 График движения некоторого тела (кривая 1) и касательная к графику при t = 5 сек (2). Скорости тела в отмеченных точках 9,5 м/с; 12,5 м/с; 30,5 м/с и 39,5 м/с; только перепуталось, какая скорость, какой точке соответствуют. |
Восстановите справедливость, заполнив таблицу соответствия между моментом времени и значением скорости тела в этот момент времени.
| Время, с | 5 | 15 | 25 | 35 |
| Скорость, м/с |
|
|
|
|
Совет: Учтите, что значение мгновенной скорости из графика можно найти, построив прямоугольный треугольник, гипотенуза которого лежит на касательной к графику в данной точке. Тогда катеты треугольника дают значения ΔX и Δt.
Летом Коля больше всего любил рыбачить, причем делал это в одном и том же месте. И вот обратил внимание, что до места рыбалки он плывет на лодке 10 мин, а возвращается назад всегда 15 мин, хотя каждый раз гребет одинаково.
Скажете, течение виновато? Да, только какова была скорость течения, если скорость лодки относительно воды 1,5 м/с?
1. 0,1 м/с 2. 0,2 м/с 3. 0,3 м/с 4. 0,4 м/с
1. 720 м; 2. 840 м; 3.900 м; 4. 1080 м.
1. 6 мин 2. 7 мин 3. 8 мин 4. 9 мин.
Из окна своей квартиры на 16 этаже Мария хорошо видела часть школьного здания и прилегающие улицы. Она даже узнавала некоторых своих одноклассников, которые с такой высоты казались совсем маленькими. Ей нравилось наблюдать за ними, оставаясь незаметной. Когда Мария заболела, и ей не надо было торопиться к началу уроков, она наблюдала и немного фантазировала…
| 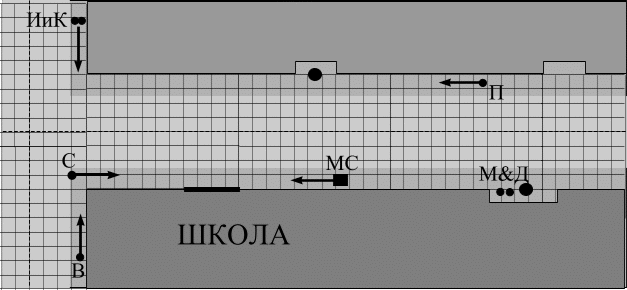 |
| Рис. 3.8 На подступах к школьным дверям незадолго до начала занятий |
Улица покрылась клеточками, как школьная тетрадь, только каждая клеточка 3х3 м; её друзья и учителя стали точками, ребята – круглыми, а Мария Степановна – квадратной. Маша всех обозначила буквами, как на уроках физики или математики.
Точка МС двигается прямолинейно, равномерно и уверенно; конечно, в положительном направлении оси х. Через 60 сек она достигнет школьной двери, до которой осталось (спасибо клеточкам) 27 м. Скорость Сидорова (С) в её системе отсчета равна -1,25 м/с.
С какой скоростью (относительно дороги) ходит в школу Сидоров?
Какова скорость Иры и Кати (ИиК) относительно точки С, если они идут относительно угла дома со скоростью 0,6 м/с?
Петров (П) двигается в три раза быстрее МС скорее по привычке; кроме того, ему надо сказать кое-что Сидорову.
Радость в глазах В (Васина) хоть и не видна с 16-го этажа, но явно присутствует; она вызвана не близостью школы, а приближением подружек ИиК на 12 м за 10 сек наблюдения.
Сколько метров прошел В за это время?
Какова скорость точки С относительно Васина, хотя последнему это совершенно безразлично?
Друзья Мишин и Дёмин (М&Д) не то, что прятались в подворотне, просто пропускали МС вперед. Интересно, в чьей системе отсчета, и с какой скоростью они перемещаются в положительном направлении, несмотря на некоторые дурные привычки?
В системе отсчета подружек ИиК со скоростью 0,6 м/с, именно они идут по направлению к школе.
Относительно Сидорова они, оставаясь на месте, перемещаются в сторону к школьным дверям.
Если бы Васин их видел, он бы подтвердил, что М&Д двигаются к школе.
Никуда они не перемещаются ни в какой системе отсчета.
Известно, что ускорение точки возникает при изменении ее скорости; но скорость – величина векторная, т. е. может измениться как по величине, так и по направлению. Ниже приводятся примеры конкретных ситуаций, в которых скорость тел изменяется, а вы определите, когда изменение скорости происходит только по величине, когда – только по направлению, когда – и то, и другое сразу.
Результаты своих размышлений занесите в таблицу.
1) Взревели турбины, и самолет, быстро набирая скорость, помчался по взлетно-посадочной полосе.
2) Держась плотной группой, велосипедисты вошли в последний поворот перед финишем.
3) Водитель резко затормозил и вывернул руль, пытаясь избежать столкновения.
4) Видимо, что-то вспомнив, баба Клава неожиданно развернулась на 1800 и пошла в обратную сторону.
5) Капли дождя барабанили по оконному стеклу, превращаясь в тоненькие ручейки, спешащие вниз.
6) Колесо аттракциона вращалось все быстрее и быстрее; пристегнутая ремнями к своему сиденью Аня с восторгом и ужасом наблюдала, как лица друзей исчезают, вливаясь в мелькающий круговорот.
Поставьте крестик или любой другой знак в клеточке, лежащей на пересечении столбца с номером ситуации и строки с характеристикой изменения скорости.
| Ситуация Изменение | 1 | 2 | 3 | 4 | 5 | 6 |
| По величине |
|
|
|
|
|
|
| По направлению |
|
|
|
|
|
|
| И то, и другое |
|
|
|
|
|
|
На рис. 3.9 показаны варианты взаимного расположения векторов скорости и ускорения для точки, движущейся по некоторой траектории. Посмотрите внимательно на рисунок, чтобы ответить на следующие вопросы:
Такое расположение векторов, в принципе, может быть, или нет?
| 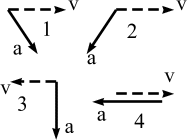 |
| Рис. 3.9 Варианты взаимного расположения векторов скорости и ускорения |
Нет, вектор ускорения либо совпадет по направлению с вектором скорости, либо противоположен ему, когда точка движется по прямой траектории. Да, такое расположение векторов вполне возможно в общем случае движения точки на плоскости.
Нет, вектор ускорения может быть только перпендикулярен вектору скорости в случае равномерного движения по окружности.
Да, такое расположение векторов возможно; только для этого точка должна увеличивать свою скорость.
Найдите среди вариантов взаимного расположения векторов скорости и ускорения на рис. 3.9 такой, который соответствует предлагаемой далее ситуации:
С радостным лаем, пес Гришка описывал круги на поляне.
Со страшным скрежетом и грохотом, автомобиль протаранил железные ворота и остановился.
Кот Барсик степенно вышагивал по направлению к сараю, но, завидев пса, рванулся вправо за угол.
Васька лихо подкатил на велосипеде к крыльцу и резко затормозил, вывернув руль вправо.
| 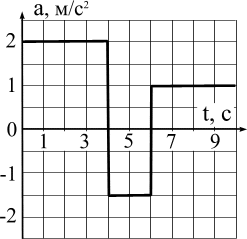 |
| Рис. 3.10 График ускорения |
График ускорения в данном случае – это зависимость проекции ускорения на направление движения от времени. Один из графиков показан на рис. 3.10. При этом движение прямолинейное и начальные условия (т. е. что было при t = 0) таковы: скорость и координата точки равны нулю.
Сообразите, как найти скорость точки в различные моменты времени и запишите, что там у вас получилось:
При t = 4 сек:
При t = 6 сек:
При t = 8 сек:
Какова координата точки в момент времени t = 8 сек?
1. 31 м 2. 34 м 3. 37 м 4. 41 м
Какова средняя скорость точки в интервале времени от 3 до 6 сек?
При t = 3 сек: v1 = 6 м/с; при t = 6 сек: v2 = 5 м/с; получаем среднюю скорость в этом интервале: (6+5):2 = 5,5 м/с.
Средняя скорость получается: (6+8+6,5+5):4 ≈ 6,38 м/с.
Находим сначала координаты точки: 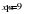 ; потом
; потом 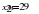 ; по формуле
; по формуле 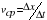 получаем: (29-9):(6-3) = 6,67 м/с.
получаем: (29-9):(6-3) = 6,67 м/с.
Среднюю скорость можно найти только при равномерном движении точки, а в данном случае движение неравномерное.
Какой была бы средняя скорость точки (в интервале времени от 3 до 6 сек), если ее начальную скорость сделать равной 8 м/с?
1. 12,5 м/с 2. 14,7 м/с; 3. 16,9 м/с 4. 19,1 м/с
Уравнения движения точки на плоскости имеют вид: 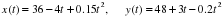 . Может, это сразу и не заметно, но траектория движения в этом случае криволинейна, точнее, представляет собой параболу.
. Может, это сразу и не заметно, но траектория движения в этом случае криволинейна, точнее, представляет собой параболу.
1. 0,25 м/с2; 2. 0,5 м/с2; 3. 0,75 м/с2; 4. 1,0 м/с2.
Можно ли считать движение равноускоренным, если с течением времени ускорение не изменяется по модулю? Почему?
Известны ли ещё частные случаи криволинейного движения, когда ускорение точки с течением времени изменяется только по направлению?
Чему равен модуль скорости точки в момент времени t = 10 сек?
В этот момент (t = 10 сек) точка разгоняется, двигаясь по своей траектории, или тормозит? Подсказка: это можно выяснить, подсчитав значение модуля скорости в этот момент времени, и в предыдущий, лучше всего, при t = 9,6 сек.
Товарный состав подходил к станции со скоростью 54 км/ч, когда машинист заметил запрещающий знак семафора, и тут же начал торможение. До семафора оставалось 400 м. На каком расстоянии от семафора окажется поезд через минуту, если движение поезда можно считать равноускоренным с ускорением 0,3 м/с2?
По формуле равноускоренного движения: 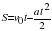 ; перемещение 15х60 – 0,3х602:2 = 360 м; т.е. осталось ещё 40 м.
; перемещение 15х60 – 0,3х602:2 = 360 м; т.е. осталось ещё 40 м.
Время движения до полной остановки:  ; t = 50 с; тогда перемещение за это время S = 375 м, остается 25 м.
; t = 50 с; тогда перемещение за это время S = 375 м, остается 25 м.
При равноускоренном движении  ; отсюда находим координату точки через минуту: -40 м.
; отсюда находим координату точки через минуту: -40 м.
Средняя скорость поезда при торможении 7,5 м/с; он успевает пройти 7,5х60 = 450 м, т. е расстояние от семафора 50 м.
Миновав, наконец, поселок, водитель вновь начал разгоняться, и на участке шоссе длиной 200 м увеличил скорость от 90 до 126 км/ч.
1. 1,0 м/с2; 2. 1,25 м/с2; 3.1,5 м/с2; 4. 1,75 м/с2.
1. 6,3 с; 2. 6,5 с; 3. 6,7 с; 4. 6,9 с.
1. 18 км/ч 2. 36 км/ч 3. 54 км/ч 4. 72 км/ч.
| |
| Рис. 3.11 Траектория движения тела, брошенного под углом 600 к горизонту. Точки на траектории показывают положения тела через каждые 0,5 сек. |
Как-то раз, стоя на балконе, Антон вспомнил, что рассказывал учитель про Галилея. Захотелось сделать что-нибудь для науки, и он бросил стальной шарик вверх под углом 600 к горизонту. Траектория движения шарика действительно была похожа на параболу, изображенную на рис. 3.11. Антон задумался, провожая шарик глазами до самого падения в песочницу (в этот момент там никого не было)
При каком условии реальная траектория шарика действительно будет точной параболой?
Движение шарика явно неравномерное; поднимаясь, шарик летел все медленнее, когда падал вниз – опять разгонялся. Каким было ускорение шарика?
В какой момент времени скорость шарика изменялась только по направлению?
Так удачно получилось, что шарик поднялся на вершину траектории ровно за полторы секунды. Это наверняка поможет вам ответить на следующие вопросы:
1. 15 м/с; 2. 17 м/с; 3. 19 м/с; 4. 21 м/с.
1. 23 м; 2. 24 м; 3. 25 м; 4. 26 м.
1. 9,7 м/с; 2. 12,1 м/с; 3.14,7 м/с; 4. 18,5 м/с.
Начинающий мотогонщик Тимофей выписывал «восьмерки» на пустыре, пугая ворон ревом двигателя. Неважно, что пока скорость не велика (5 м/с), зато движение равномерное. То по большой окружности, то по малой, как показано на рис. 3.12
Если тело движется по окружности равномерно, будет ли у него ускорение?
Нет, ускорение возникает только тогда, когда скорость изменяется.
Да, потому что изменяется направление вектора скорости.
Нет, потому что вектор скорости направлен по касательной к траектории движения.
Да, будет постоянное по величине и направлению центростремительное ускорение.
-
|
| Рис. 3.12 Трасса для тренировок начинающего мотогонщика. |
На рис. 3.12 точками а, б, в, г обозначены некоторые характерные положения мотогонщика на трассе. Но при этом возникают вопросы:
В какой из отмеченных точек ускорение будет наибольшим и чему оно равно?
В точке (в) мотоциклист переходит с одной окружности на другую; каким тогда будет именно в этой точке центростремительное ускорение?
При равномерном движении по окружности, как известно, модуль ускорения не изменяется. А вот среднее ускорение в некотором интервале времени? Заметьте: радиусы окружностей отличаются в два раза, поэтому из точки (а) в точку (б) тело перемещается за то же время, что требуется для перемещения из точки (в) в точку (г).
Найдите среднее ускорение тела на участке (а – б) трассы. Прямо по определению:  . Только надо вспомнить, как вычитаются векторы, и как найти время, если знаешь путь и скорость
. Только надо вспомнить, как вычитаются векторы, и как найти время, если знаешь путь и скорость
Найдите (точно также) среднее ускорение тела на участке (в – г).
В каком случае ускорение получается больше?
Кинематика твердого тела
Ниже перечисляются тела, достаточно сложные, но которые вам наверняка знакомы. Попробуйте их расставить (т. е. указать номера) в порядке приближения по своим свойствам к модели абсолютно твердого тела.
Бетонный блок, забытый строителями у края дороги.
Старый футбольный мяч, немного спущенный.
Сваленная в углу старая рыболовная сеть.
Доска двадцатимиллиметровая.
Надувной матрас.
Приведены ситуации, когда какое-то сложнее тело как-то двигается. Вам надо опознать, в каких видах движения оно участвует: а) в поступательном; б) вращательном; в) поступательном и вращательном вместе; г) в более сложных видах движения. Результаты своего расследования занесите в таблицу.
При замедленном воспроизведении видеозаписи испытаний было видно, как после удара автомобиля о бетонную стену корежится и разрывается его корпус.
Раздался выстрел стартового пистолета, и спортсмены рванулись вперед по гаревой дорожке.
Брошенная палка, неторопливо вращаясь в воздухе, описала плавную дугу и упала у самой кромки воды.
Веч ер был чудесный, и ребята любовались парком с высоты птичьего полета из кабины колеса обозрений, медленно добиравшейся до наивысшей точки траектории.
Мотор еще раз надрывно взревел, заднее колесо, вращаясь в грязи, чуть ли не дымилось, но автомобиль не сдвинулся с места ни на миллиметр.
Виктор впервые участвовал в групповом прыжке с парашютом, но, распластавшись во встречном потоке воздуха, быстро сумел развернуть свое тело в нужную сторону.
| Ситуация Движение | 1 | 2 | 3 | 4 | 5 | 6 |
| Поступательное |
|
|
|
|
|
|
| Вращательное |
|
|
|
|
|
|
| Поступательное и вращательное |
|
|
|
|
|
|
| Более сложное движение |
|
|
|
|
|
|
Родители подарили велосипед, чтобы Вася хорошо учился. Хорошо катиться по лесной тропинке, плавно вращая педали, и лишь время от времени переключая скорости рычажком на руле! Но Вася обещал, и, чтобы совместить приятное с полезным, размышлял о физике.
| |
| Рис. 3.13.Задняя часть велосипеда |
Если велосипед катится прямолинейно и равномерно, то:
Какие части велосипеда (Васю не будем трогать) двигаются поступательно, какие – вращаются?
Почему педали вращаются, но при этом их движение поступательно?
Какие точки на велосипеде двигаются с ускорением, хотя весь велосипед двигается равномерно и прямолинейно?
Какие точки велосипеда двигаются (относительно дороги) вдвое быстрее, чем весь велосипед в целом?
Все понимают, что на ровной (горизонтальной) дороге велосипед движется потому, что кто-то вращает педали. И, чем быстрее вращает, тем быстрее едет.
Какая шестерня (1 или 2) вращается быстрее, если цепь не соскакивает?
Может ли заднее колесо вращаться быстрее (медленнее) задней шестерни? В любом случае, почему?
С какой угловой скоростью вращаются педали, если за секунду они совершают полный оборот?
1. 1 с-1 2. 6,3 с-1 3. 360 с-1 4.3,1 с-1.
Если вращать педали с частотой 60 об/мин, то с какой скоростью будет катиться велосипед по ровной дороге? Для справки: у ведущей шестерни(1) 41, а у ведомой(2) – 16 зубьев; диаметр D заднего колеса равен 650 мм.
Угловая скорость вращения педалей  ; тогда скорость оси колеса
; тогда скорость оси колеса  ; получаем 2,0 м/с.
; получаем 2,0 м/с.
Надо еще учесть, что маленькая шестерня (вместе с задним колесом) вращается медленнее в 41/16 раза, тогда получим 0,8 м/с.
Цепь заставляет меньшую шестерню вращаться быстрее в 41/16 раза, скорость велосипеда примерно 18,8 км/ч.
Скорость велосипеда примерно 20-25 км/ч.
В каждое мгновенье колесо касается дороги другим (небольшим) участком поверхности шины; назовем эти участки точками касания.
Какова скорость точки касания колеса относительно дороги, если проскальзывание отсутствует?
Чему равно центростремительное ускорение точек касания?
| |
| Рис. 3.14 Труба, которая катится по горизонтальной поверхности |
По гладкой горизонтальной поверхности с некоторой скоростью v катится труба, радиус которой обозначим R. При этом точка касания А не проскальзывает по поверхности опоры. У какой точки (А, В, С или D) на внешней поверхности самой трубы скорость относительно дороги будет а) наибольшей; б) наименьшей; в) такой же?
Если радиус трубы 25 см и катится она со скоростью 0,8 м/с, то с какой угловой скоростью она при этом вращается?
1. 3,2 1/с. 2. 20 1/с 3. 31,25 1/с 4. 0,2 1/с
| |
| Рис. 3.15 Векторы скоростей точек на поверхности трубы |
На рис. 3. 15 показаны возможные варианты векторов скорости точек на поверхности трубы.
Попробуйте опознать среди них те, что принадлежат точкам В, С и D.
В каком случае скорость точки В была бы представлена вектором 1? А вектором 5?
За счет вращения трубы, точки на её поверхности двигаются с центростремительным ускорением.
Какой из векторов (1 – 6) правильно показывает направление ускорения точки А?
Для трубы радиусом 25 см, ось которой движется со скоростью 0,8 м/с, центростремительное ускорение точки D будет равно
1. 16 м/с2 2. 2,56 м/с2 3. 0,39 м/с2 4. 0,16 м/с2.
Динамика Законы механики Ньютона
Так уж устроен мир, что все тела, так или иначе, взаимодействуют друг с другом. Иногда это взаимодействие очевидно (например, в городском транспорте в часы «пик»), иногда – не очень. Именно взаимодействие тел определяет все особенности их движения.
Опираясь на свой житейский опыт и смутные воспоминания о прошлогодних уроках физики, постарайтесь ответить на следующие вопросы:
Правда ли, что если скорость какого-нибудь тела изменилась, то значит что-то (или кто-то) подействовал на это тело?
Бывает такое в жизни: кирпич никуда не двигается, хотя на него явно действуют другие тела. Если «нет», то почему; если «да», то когда.
Говорят, если скорость какого-нибудь тела изменилась, то виноваты в этом окружающие тела. Петя, пока ждал Марину, несколько раз проверял: и разгонялся, и тормозил, и поворачивал в разные стороны. Все прекрасно получалось, хотя никого и близко рядом не было. Как это объяснить?
Если вы помните, для описания движения тел используется система отсчета (тело отсчета, система координат, часы). Систем отсчета можно придумать бесконечно много, и в каждой из них движение некоторого тела, вообще говоря, будете выглядеть по-разному.
В каких системах отсчета тело сохраняет состояние покоя, или равномерного прямолинейного движения, если влияние других тел на него скомпенсировано?
Любой наблюдатель воспринимает движение в окружающем мире в своей собственной системе отсчета. Маша сидела на заднем сиденье автобуса и хорошо видела, как повалились вперед стоящие пассажиры, хотя их никто не толкал. Будет ли Машина система отсчета инерциальной?
Будет ли (строго говоря) инерциальной система отсчета, связанная с Землей и которой мы обычно пользуемся при описании движения различных тел, если учесть, что Земля вращается?
Петя коротал время в городском транспорте, сочиняя фантастический роман. Он как раз обдумывал сцену, в которой герои беседовали, шагая по длинным коридорам межзвездного космического корабля. Сам корабль имел форму огромного (несколько километров в поперечнике) «бублика», вращающегося вокруг своей оси с определенной угловой скоростью.
Надо ли прикладывать особые усилия, чтобы шагать прямолинейно и равномерно по коридору этого космического корабля? Почему?
Зависит ли ответ от того, как ориентирован коридор в космическом корабле (например, по радиусу, или по окружности корабля)
Какие тела могут действовать на экипаж корабля, если до других космических тел огромные расстояния?
Выполняется ли на этом космическом корабле первый закон Ньютона, он же закон инерции?
Как называется векторная физическая величина, являющаяся количественной мерой взаимодействия тел. Примечание: наличие таковой (вопреки известной поговорке) не связано с пониженными требованиями к умственным способностям индивидуума.
Почему говорят, что истинные силы всегда появляются парами?
Как в принципе можно сравнивать силы между собой?
Вася уверял товарищей, что он как-то поднимал штангу 140 кг (правда, так и не поднял).
Означает ли это, Васина сила была равна силе тяжести штанги? Ведь, если на тело действуют две силы, направленные вдоль одной прямой в разные стороны, а ускорение не появляется, то они равны! Поясните.
Если силы появляются парами, то какие силы составят пару для силы Васиных рук, для силы тяжести штанги? Или они сами себе пара?
Петя внимательно перечитал абзац учебника про то, как измеряют силу пружинным динамометром, но так и не понял: как люди узнали, что величина силы пропорциональна растяжению пружины?
|
|
| Рис. 3.16 Схема опыта по определению ускорения тележки |
Лабораторная работа была совсем несложная, тем более, Миша с Петей упростили её, выкинув (по сравнению с вариантом из учебника) динамометр. Схема опыта показана на рис. 3.16. Тележку разгоняет груз, подвешенный на другом конце нити; число гирек изменялось от 1 до 5. Ребята полагали, что это приводит к изменению силы, действующей на тележку. Измеряли время t, за которое тележка перемещалась на S; ускорение определяли по формуле

. Результаты опыта, т. е. зависимость ускорения от числа грузов, показана на рис. 3.16.
Верны ли рассуждения ребят, о том, что сила, действующая на тележку, пропорциональна числу гирек?
Да, потому, что гирьки одинаковые, и общая сила тяжести точно пропорциональна числу гирек.
Нет, потому что сила тяжести направлена вертикально вниз, а тележка движется горизонтально вправо.
Да, потому что помешать могла только сила трения, а при использовании тележки на легких колесиках она была очень мала.
Нет, потому что сила тяжести гирек разгоняет не только тележку, но и сами гирьки.
| |
| Рис. 3.17 График зависимости ускорения тележки, м/с2, от числа гирек. |
Каким бы вы ожидали увидеть график зависимости ускорения тела от действующей на него силы из теоретических соображений?
Оправдывают ли ваши ожидания результаты опыта: в зависимости от числа гирек ускорение равно 1,08; 1,91; 2,52; 2,96; 3,76 м/с2; см. также график соответствующей зависимости на рис. 3.17.
По каким причинам в опыте не получилась прямо пропорциональная зависимость между ускорением и действующей на тело силой?
Если в проводимом опыте нить, которая разгоняет тележку и вдоль которой направлен вектор силы, не будет параллельна поверхности стола, например, пойдет вверх от тележки
Тележка по-прежнему будет двигаться по поверхности стола, или полетит вслед за нитью?
А если вектор ускорения будет направлен вдоль поверхности стола, то тогда векторы  уже не будут совпадать по направлению! Как все это объяснить?
уже не будут совпадать по направлению! Как все это объяснить?
Петя и раньше был в курсе, что масса есть мера инертности тела: чем больше (меньше) масса, тем труднее (легче) разогнать тело, остановить, или повернуть. Но после прочтения учебника2 (стр. 66) вкралось сомнение. Если массой назвали отношение  , то отсюда очевидно следует соотношение
, то отсюда очевидно следует соотношение  , которое уже называют законом механики, точнее, вторым законом Ньютона.
, которое уже называют законом механики, точнее, вторым законом Ньютона.
Петя почувствовал себя обманутым: с таким же успехом можно было бы назвать массой отношение  ; тогда бы и закон изменился; получилось бы
; тогда бы и закон изменился; получилось бы  ?? Что вы об этом думаете?
?? Что вы об этом думаете?
Страницы учебника – это святое; нужно верить, а не сомневаться.
Вероятно, есть еще какие-то аргументы, кроме упомянутых в учебнике, в пользу указанного определения массы.
Больше делать, что ли нечего, кроме как учебник критиковать!
Все-таки большая масса – это что-то огромное (поезд, например), что трудно разогнать или остановить.
Что верно, а что не верно из того, что можно предположить, исходя из определения массы из учебника: 
Проще всего увеличить массу, уменьшив ускорение тела; можно даже сделать ее сколь угодно большой! Правильно?
Если немного не хватает силы  , надо просто чуть-чуть увеличить массу! Правильно?
, надо просто чуть-чуть увеличить массу! Правильно?
Ускорение, с которым движется тело, прямо пропорционально действующей силе и обратно пропорционально массе тела. Правильно?
Пробираясь к выходу переполненного автобуса с рюкзаком за плечами, Вася (масса 96 кг без рюкзака) популярно объяснял смысл 3-го закона Ньютона возмущающимся пассажирам.
Правда ли, что при взаимодействии двух тел на каждое из них действуют одинаковые по модулю силы?
Т. е. с какой силой Васин локоть действовал под ребро старушки, с такой же силой старушка своим ребром действовала на Васин локоть?
На улицах города произошло ДТП – огромный джип цвета катафалка столкнулся с бледно – бирюзовой «Окой». К счастью, обошлось без жертв, были только пострадавшие.
На какой из автомобилей действовала большая (меньшая) сила в момент удара, если вспомнить 3-й закон Ньютона?
В каком из этих двух автомобилей вы предпочли бы оказаться в момент столкновения?
С какой силой ударил по мячу (массой примерно 0,4 кг) нападающий Катапультов, если он (мяч) сорвался с места с ускорением 450 м/с2?
1. 275 Н; 2. 220 Н; 3. 180 Н; 4. 140 Н.
Под действием силы F = 2,5 Н лежащий на столе брусок приобретает ускорение 0,3 м/с2. Если силу увеличить в два раза, то ускорение
Будет больше в 2 раза (по 2 закону Ньютона), т. е. 0,6 м/с.
Ускорение увеличится, но больше, чем в 2 раза (из–за трения).
Ускорение увеличится, но меньше, чем в 2 раза (из–за трения).
Ускорение зависит от массы тела, которая не указана.
Может ли ускорение тела не совпадать с направлением силы, приложенной к телу?
Нет, на основании 2 закона Ньютона
Да, если сила достаточно велика.
Да, если на тело действуют и другие силы.
Нет, это противоречит 1 закону Ньютона.
Санки массой 10 кг, двигаясь под уклон 30 0, приобретают ускорение 4 м/с2. Равнодействующая всех сил, приложенных к телу, равна
20 Н, направлена вниз.
40 Н, направление совпадает с направлением ускорения.
Зависит от силы трения, которая не указана.
40 Н, направлена вниз.
Девочка катается на качелях. В момент прохождения положения равновесия равнодействующая всех сил, действующих на девочку, направлена
Вертикально вниз, как сила тяжести
По касательной к траектории, как тангенциальное ускорение
Вверх, к точке подвеса, как нормальное ускорение
Равнодействующая всех сил равна нулю.
Два бруска с массами 400 г и 300 г и одинаковой поверхностью связаны нерастяжимой невесомой нитью и могут двигаться под действием горизонтальной силы F = 3,5 Н. Сила натяжения нити, связывающей бруски, может быть равна
F = 3,5 Н, т. к. двигаются оба бруска.
Все зависит от силы трения, которая неизвестна.
Половине действующей силы, т. е. 1,75 Н.
1,5 Н или 2 Н, в зависимости от того, какой брусок впереди.
1� Физика: Учеб. Для 10 кл. общеобразоват учреждений/ Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. – 11-е изд. – М.: Просвещение,2003. – 336 с. – ил
2� Физика: Учеб. Для 10 кл. общеобразоват учреждений/ Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. – 11-е изд. – М.: Просвещение,2003. – 336 с. – ил

 Получите свидетельство
Получите свидетельство Вход
Вход




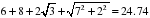 , если, конечно, немного округлить.
, если, конечно, немного округлить.

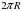 )
)

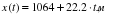 ; 2.
; 2. 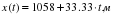
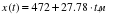 ; 4.
; 4. 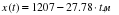

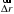 к интервалу времени
к интервалу времени 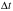 , за которое это перемещение произошло (на криволинейной траектории)
, за которое это перемещение произошло (на криволинейной траектории)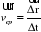 ; тогда модуль средней скорости равен 340/20 = 17 м/с.
; тогда модуль средней скорости равен 340/20 = 17 м/с.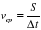 ; т. е. 360/20 = 18 м/с.
; т. е. 360/20 = 18 м/с.



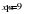 ; потом
; потом 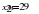 ; по формуле
; по формуле 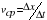 получаем: (29-9):(6-3) = 6,67 м/с.
получаем: (29-9):(6-3) = 6,67 м/с.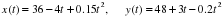 . Может, это сразу и не заметно, но траектория движения в этом случае криволинейна, точнее, представляет собой параболу.
. Может, это сразу и не заметно, но траектория движения в этом случае криволинейна, точнее, представляет собой параболу.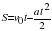 ; перемещение 15х60 – 0,3х602:2 = 360 м; т.е. осталось ещё 40 м.
; перемещение 15х60 – 0,3х602:2 = 360 м; т.е. осталось ещё 40 м.








 Контрольные вопросы и задания по основным разделам школьного курса механики (0.26 MB)
Контрольные вопросы и задания по основным разделам школьного курса механики (0.26 MB)
 0
0 781
781 107
107 Нравится
0
Нравится
0


