I. Паспорт комплекта контрольных измерительных материалов.
1. Область применения комплекта контрольных измерительных материалов.
Контрольные измерительные материалы (КИМ) предназначены для контроля и оценки образовательных достижений обучающихся, освоивших программу
учебной дисциплины «Математика».
КИМ включают контрольные материалы для проведения текущего
контроля и промежуточной аттестации в форме экзамена.
КИМ разработаны на основании основной профессиональной образовательной программы по профессии СПО; программы учебной дисциплины «Математика».
| Результаты освоения
| Основные показатели оценки результата и их критерии | Тип задания; № задания
| Форма аттестации (в соответствии с учебным планом) |
| Умение решать задачи алгебры и начал анализа, геометрии | вычислять производные и первообразные элементарных функций, используя справочные материалы; исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа; вычислять в простейших случаях площади с использованием первообразной. распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями; описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении; анализировать в простейших случаях взаимное расположение объектов в пространстве; изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач; строить простейшие сечения куба, призмы, пирамиды; решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); использовать при решении стереометрических задач планиметрические факты и методы; проводить доказательные рассуждения в ходе решения задач. | Самостоятельная работа Тестирование Домашняя работа Устный опрос Контрольная работа | Экзамен |
| Умение применять различные методы для решения уравнений, неравенств и их систем | решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения и их системы; составлять уравнения и неравенства по условию задачи; использовать для приближенного решения уравнений и неравенств графический метод; изображать на координатной плоскости множества решений простейших уравнений и их систем.
| Самостоятельная работа Тестирование Домашняя работа Устный опрос Контрольная работа | Экзамен |
| Умение решать вероятностные и статистические задачи | решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул; вычислять в простейших случаях вероятности событий на основе подсчета числа исходов.
| Самостоятельная работа Тестирование Домашняя работа Устный опрос
| Экзамен |
2.Контрольные измерительные материалы для проведения текущего контроля.
2.1Диагностическая контрольная работа.
Перечень объектов контроля и оценки: У1, У2, У3, У4, У5, У23
Текст задания
Вариант 1
Упростить выражение 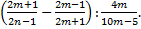
Решить неравенство: 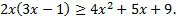
3. Решить систему уравнений: 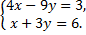
4.Соотнесите квадратные уравнения и их корни.
| 1) х2+5х-6=0. | 2) х2-6х+9=0 | 3) х(х-2)=0 |
| А) х1=1, х2= - 6 | Б)х1= 0, х2= 2 | В) х= 3 |
Ответ:
5.Решите уравнение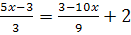
6.Площадь прямоугольника АВСD равна 15. Найдите сторону ВС прямоугольника, если известно, что АВ = 3.
7.В прямоугольном треугольнике АВК гипотенуза АВ равна 13, катет АК равен 12, катет ВК равен 8. Найдите тангенс угла А.
Вариант 2
1.Упростить выражение 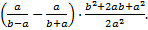
2. Решить неравенство: 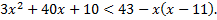
3.Решить систему уравнений: 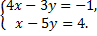
4.Соотнесите квадратные уравнения и их корни
| 1) х2= 4 | 2) х2-7х+6 = 0 | 3) 2х2+3х -14 = 0 |
| А) х1= 1, х2= 6 | Б) х1= - 2, х2= 2 | В) х1= - 3,5 , х2= 2 |
Ответ:
5.Решите уравнение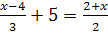
6.Площадь параллелограмма АВСD равна 45. Найдите сторону ВС параллелограмма, если известно, что высота, проведенная к этой стороне, равна 5.
7. В прямоугольном треугольнике АВК гипотенуза АВ равна 17, катет АК равен 15, катет ВК равен 8. Найдите cинус угла А.
Время на выполнение: 45 мин.
Критерии оценивания:
За верное решение каждого из заданий выставляется 1 балл. 7 баллов - оценка- 5; 5-6 баллов – 4; 3-4 балла - 3
2.2 Контрольная работа № 1 по теме: «Корни, степени и логарифмы».
Перечень объектов контроля и оценки: У1, У2, У3, У6
Текст задания
Вариант – 1
1. Вычислите 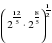
2. Вычислите 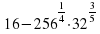
3. Вычислите 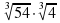 –
– 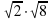
4 .Вычислите 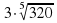 ·
· 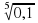
5 .Вычислите log2112 – log2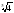 - log2 7.
- log2 7.
6 .Вычислите log2108 – log227 – log5 125.
7. Вычислите 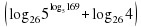 2 –
2 – 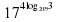
Вариант – 2
1. Вычислите 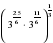 .
.
2. Вычислите 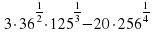
3. Вычислите 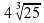 · 2
· 2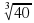
4 .Вычислите 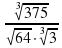
5 .Вычислите log5 75 + lg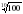 - log5 15.
- log5 15.
6 .Вычислите log20,4 + log2√2 + log2 10.
7. Вычислите 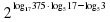
Вариант – 3
1.Вычислите 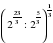 .
.
2. Вычислите ;
3.Вычислите 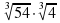 –
– 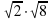 ..
..
4 .Вычислите  .
.
5.Вычислите 
6.Вычислите log2108 – log227 – log5 125.
7. Вычислите 
Время на выполнение: 45 мин.
Критерии оценивания:
За верное решение каждого из заданий выставляется 1 балл. 7 баллов - оценка- 5; 5-6 баллов – 4; 3-4 балла – 3
2.3 Контрольная работа № 2 «Параллельность и перпендикулярность прямых и плоскостей в пространстве».
Перечень объектов контроля и оценки: У19, У20, У23, 24, У25, У26
Текст задания
Вариант 1
1.Расстояние от некоторой точки до плоскости квадрата равно 4 см, а до каждой из его вершин 6 см. Найдите диагональ квадрата.
2.Из вершины равностороннего треугольника АВС проведен перпендикуляр АК к плоскости треугольника. Точка Д – середина стороны ВС. Найдите длину АК, если ВС равно  см, а КД равно 8 см.
см, а КД равно 8 см.
3. Через концы отрезка АВ, не пересекающего плоскость α, и точку С – середину этого отрезка, проведены параллельные прямые, пересекающие плоскость α в точках А1, В1 и С1 соответственно. Найдите длину отрезка СС1, если АА1 = 12 см, а ВВ1 = 6 см.
4. Плоскость α, параллельная стороне ВС треугольника АВС, пересекает стороны АВ и АС в точках М и Н соответственно. Найдите длину отрезка ВС, если МН = 6 см, а АМ : МВ = 3 : 5.
5.Из точки, отстоящей от плоскости на расстоянии 4, проведены две наклонные к плоскости под углом 45 0. Найдите длины наклонных.
Вариант 2
1.Расстояние от некоторой точки до плоскости прямоугольника равно  см, а до каждой из его вершин 3 см. Найдите диагональ прямоугольника.
см, а до каждой из его вершин 3 см. Найдите диагональ прямоугольника.
2.Расстояния от вершин А, В, С параллелограмма АВСД, не пересекающего плоскость α, до плоскости α равны соответственно 14 см, 11 см и 4 см. Найдите расстояние от вершины Д до плоскости α.
3. Через концы отрезка МН, не пересекающего плоскость α, и точку К – середину этого отрезка, проведены параллельные прямые, пересекающие плоскость α в точках М1, Н1 и К1 соответственно. Найдите длину отрезка НН1, если ММ1 = 12 см, а КК1 = 6 см.
4. Плоскость α, параллельная стороне НМ треугольника НМК, пересекает стороны МК; и КН в точках Д и В соответственно. Найдите длину отрезка ВД, если МН = 14 см, а НВ : ВК = 4 : 3.
5.Из точки, отстоящей от плоскости на расстоянии 10, проведены две наклонные, образующие с плоскостью углы 60 0. Найдите сумму длин наклонных.
Вариант 3
1.Из вершины равностороннего треугольника АВС проведен перпендикуляр АК к плоскости треугольника. Найдите длину АК, если ВС равно 3 см, а КС равно  см.
см.
2.Расстояния от вершин А, В, С параллелограмма АВСД, не пересекающего плоскость α, до плоскости α равны соответственно 19 см, 6 см и 16 см. Найдите расстояние от вершины Д до плоскости α.
3. Через концы отрезка ЕР, не пересекающего плоскость α, и точку Л – середину этого отрезка, проведены параллельные прямые, пересекающие плоскость α в точках Е1, Р1 и Л1 соответственно. Найдите длину отрезка РР1, если ЕЕ1 = 4 см, а ЛЛ1 = 14 см.
4.Плоскость α, параллельная стороне КЛ треугольника СКЛ, пересекает стороны ЛС и КС в точках Р и Д соответственно. Найдите длину отрезка РД, если КЛ = 27 см, а КД : ДС = 7 : 2.
5.Из точки, отстоящей от плоскости на расстоянии 5, проведены две наклонные, образующие с плоскостью углы 30 0. Найдите сумму длин наклонных.
Время на выполнение: 45 мин.
Критерии оценивания:
За верное решение каждой из задач выставляется 1 балл.
За неверное решение задачи выставляется 0 баллов.
2.4 Контрольная работа № 3 по теме «Векторы в пространстве »
Перечень объектов контроля и оценки: У1, У18, У19
Текст задания
Вариант – 1
1.Точка М середина отрезка АВ. Найдите координаты точки В, если А(1; 3; -2), М(-2; 4; 5)..
2.Найти угол между векторами АВ и ВС, если А (1; - 1; 1), В ( 4; 2; 2), С ( 3; 0; 1)
3.Даны  . Найдите координаты вектора
. Найдите координаты вектора  .
.
4.Даны . Найдите скалярное произведение векторов.
. Найдите скалярное произведение векторов.
5.Даны точки А(0;4;–1), В(1;3;0),С(0;2;5). Найдите длину вектора  .
.
6.Найдите значения m и n, при которых векторы  и
и  коллинеарны.
коллинеарны.
Вариант – 2
1.Точка М середина отрезка АВ. Найдите координаты точки М, если А(1; 3; -2), В(- 5; 7; 8).
2.Найти угол между векторами АВ и ВС, еслиА (2; 0; 1), В ( 1; 3; 6), С ( 1; 8; 3)
3.Даны точки А(2;4;–1), В(1;3;2),С(1;2;5). Найдите длину вектора  .
.
4.Даны  . Найдите координаты вектора
. Найдите координаты вектора 
5Даны векторы  {5; 3; -2},
{5; 3; -2},  {1; 2; -3}. Найдите скалярное произведение векторов
{1; 2; -3}. Найдите скалярное произведение векторов
6.Найдите значения m и n, при которых векторы  и
и  коллинеарны.
коллинеарны.
Вариант 3
1.Точка М середина отрезка АВ. Найдите координаты точки В, если А(4; - 6; 2), М(5; - 3; 0).
2.Найти угол между векторами АВ и ВС, еслиА (2; 0; 1), В ( 0; - 1; 4), С ( 3; - 1; - 2)
3.Даны векторы  {3; 1; -2},
{3; 1; -2},  {1; 4; -3}. Найдите скалярное произведение векторов
{1; 4; -3}. Найдите скалярное произведение векторов
4.Даны  . Найдите координаты вектора
. Найдите координаты вектора  .
.
5.Даны точки А(1;4;–1), В(1;3;4),С(3;2;2). Найдите длину вектора  .
.
6.Найдите значения m и n, при которых векторы  и
и  коллинеарны.
коллинеарны.
Время на выполнение: 45 мин.
Критерии оценивания:
За верное решение каждого из заданий выставляется 1 балл. 6 баллов - оценка- 5; 5 баллов – 4; 3-4 балла - 3
2.5 Контрольная работа № 4 по теме: «Основы тригонометрии».
Перечень объектов контроля и оценки: У2, У3, У4
Текст задания
Вариант – 1
1.Вычислите значение cos2 , если sin
, если sin = –
= –  и
и 
2.Упростите выражение – 4sin2x + 5 – 4cos2x
3.Найдите значение выражения при cos =
= 
4.Упростите выражение  .
.
5.Вычислите значение cos( +
+ ), если cos
), если cos =-
=- , sin
, sin =
= ,
,  ; 0.
; 0.
6.Найдите значение выражения  .
.
Вариант – 2
1. Вычислите значение sin2x, если cosx = и
и 
2.Упростите выражение 5sin2x – 4 + 5cos2x
3.Найдите значение выражения при 
4.Упростите выражение  .
.
5.Вычислите значение sin( -
- ), если cos
), если cos =-
=- , sin
, sin =
= ,
,  ;
;  .
.
6.Вычислите: 
Вариант – 3
1. Упростите выражение  .
.
2.Вычислите значение sin( +
+ ), если cos
), если cos =-
=- , sin
, sin =
= ,
,  ;
;  .
.
3.Упростите выражение  .
.
4. Вычислите  .
.
5.Найдите  , если
, если 
6.Вычислите: cos 28
 ;
;
Время на выполнение: 45 мин.
Критерии оценивания:
За верное решение каждого из заданий выставляется 1 балл. 6 баллов - оценка- 5; 5 баллов – 4; 3-4 балла - 3
2.6 Контрольная работа № 5 по теме: «Функции»
Перечень объектов контроля и оценки: У4, У5, У6, У7.
Текст задания
Вариант – 1
1.Построить график функции 
а) перечислите свойства этой функции;
б) найдите наибольшее и наименьшее значение функции на отрезке [-3;0].
2.Решите графически уравнение:3х = 2х + 3.
3.Найти ООФ 
4.Найдите функцию, обратную к функции  .
.
Постройте график данной функции и график обратной к данной функции;
укажите область определения и множество значений каждой из них.
5.Решите графически уравнениеlog1/2x = – 0,5x + 1
Вариант – 2
1.Построить график функции
а) перечислите свойства этой функции;
б) найдите наибольшее и наименьшее значение функции на отрезке [4;7].
2.Решите графически уравнение:(1/2)х = 2 – х.
3.Найти ООФ:
4. Найдите функцию, обратную к функции: .
.
Постройте график данной функции и график обратной к данной функции;
укажите область определения и множество значений каждой из них.
5.Решите графически уравнение:log3x = 2x – 3
Время на выполнение: 45 мин.
Критерии оценивания:
За правильный ответ каждого из заданий выставляется 1 балл.
За неправильный ответ выставляется 0 баллов
2.7 Контрольная работа № 6 по теме «Многогранники»
Перечень объектов контроля и оценки:У20, У22, У23, 24, У25, У26
Текст задания
Вариант – 1
1.Найдите боковую поверхность правильной треугольной пирамиды, если сторона основания равна 2 см, а все двугранные углы при основании 30 0.
2.Боковая поверхность правильной четырехугольной призмы равна 16 см 2, а полная поверхность 48 см 2. Найдите высоту призмы.
3. Найдите боковое ребро правильной четырехугольной пирамиды, если ее объем равен 12 см3, а сторона основания равна 3 см.
4.В пирамиде DABC ребро АD перпендикулярно основанию, AD = см,
АВ = 2 см, угол АВС - прямой, угол ВАС равен 600, М - середина отрезка АD.
Найдите площадь боковой поверхности пирамиды.
5.В прямоугольном параллелепипеде длина диагонали 4 см, длины его измерений относятся как 1: 2 : 4. Найти площадь полной поверхности параллелепипеда.
см, длины его измерений относятся как 1: 2 : 4. Найти площадь полной поверхности параллелепипеда.
Вариант – 2
1.Боковая поверхность правильной треугольной призмы равна  см2, а полная поверхность
см2, а полная поверхность  см 2. Найдите высоту призмы.
см 2. Найдите высоту призмы.
2.Найдите боковую поверхность правильной четырехугольной пирамиды, если сторона основания равна  см, а все двугранные углы при основании 45 0.
см, а все двугранные углы при основании 45 0.
3.Диагональ правильной четырёхугольной призмы равна 4 и наклонена к плоскости основания под углом 450 . Найдите площадь диагонального сечения.
4.В прямой призме ABCА1В1С1 угол АВС - прямой, угол САВ равен 600,
AВ = 2 см, AА1 = см.
Найдите площадь полной поверхности прямой призмы.
5.Стороны основания прямого параллелепипеда равны 8 см и 15 см и образуют угол в 60˚. Меньшая из площадей диагональных сечений равна 130 см2. Найти площадь полной поверхности параллелепипеда
Вариант 3
1.Боковая поверхность правильной четырехугольной призмы равна 48 см 2, а полная поверхность 56 см 2. Найдите высоту призмы.
2.Найдите боковую поверхность правильной треугольной пирамиды, если сторона основания равна 2 см, а все двугранные углы при основании 60 0.
3. Найдите боковое ребро правильной четырехугольной пирамиды, если ее объем равен 4 см3, а сторона основания равна 2 см.
4.Найдите высоту правильной четырёхугольной усечённой пирамиды, если стороны её основания равны 6 см и 3 см, а боковая поверхность равновелика сумме оснований.
5.В прямой призме основанием является параллелограмм со сторонами 4 м и 5 м и углом между ними 30˚. Найти площади боковой и полной поверхностей призмы, если её высота равна 7 м.
Время на выполнение: 45 мин.
Критерии оценивания:
За верное решение каждой из задач выставляется 1 балл.
За неверное решение задачи выставляется 0 баллов.
2.8 Итоговая контрольная работа № 1 за 1-ый курс.
Перечень объектов контроля и оценки:У1, У2, У3, У6, У19, У21, У20, У23, У24, У26
Текст задания
Вариант – 1
1.Найдите значение выражения +
+
2. Вычислите 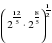 .
.
3.Вычислите 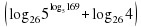 2 –
2 – 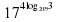
4.В прямоугольном параллелепипеде АВСДА1В1С1Д1 известно, что Д1В = 
 , ВВ1= 3, А1Д1 =4. Найдите длину ребра А1В1.
, ВВ1= 3, А1Д1 =4. Найдите длину ребра А1В1.
5.Найдите sinα, еслиcosα = - 0,6 и 
6. Плоскость α, параллельная стороне ВС треугольника АВС, пересекает стороны АВ и АС в точках М и Н соответственно. Найдите длину отрезка ВС, если МН = 6 см, а АМ : МВ = 3 : 5.
7.Из точки, отстоящей от плоскости на расстоянии 4, проведены две наклонные к плоскости под углом 45 0. Найдите длины наклонных.
8.Найдите значение выражения 
9.Найдите x, если 
10.Найдите область определения функции 
Вариант – 2
1.Найдите значение выражения:
2.Вычислите 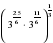
3.Вычислите log5 75 + lg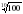 - log5 15.
- log5 15.
4.В правильной четырехугольной пирамиде РАВСД точка О - центр основания, точка Р – вершина, РО = 24, АС = 14.Найдите боковое ребро РД.
5.Найдите cosα, еслиsinα = 0,8 и 
6. Плоскость α, параллельная стороне КЛ треугольника СКЛ, пересекает стороны ЛС и КС в точках Р и Д соответственно. Найдите длину отрезка РД, если КЛ = 27 см, а КД : ДС = 7 : 2.
7.Из точки, отстоящей от плоскости на расстоянии 5, проведены две наклонные, образующие с плоскостью углы 30 0. Найдите сумму длин наклонных.
8.Найдите значение выражения 
9.Найдите область определения функции  .
.
Время на выполнение: 90 мин.
Критерии оценивания:
За верное решение каждого из заданий выставляется 1 балл. 10 баллов - оценка- 5; 8-9 баллов – 4; 6-7 баллов – 3
2.9 Контрольная работа № 1/2 по теме «Тела и поверхности вращения»
Перечень объектов контроля и оценки:У20, У22, У23, 24, У25, У26
Текст задания
Вариант – 1
1. Образующая конуса наклонена к плоскости основания под углом 300 и равна 8 см. Найдите площадь осевого сечения конуса.
2.Найдите расстояние от центра шара до плоскости сечения, если радиус шара равен 6 см, а радиус сечения равен 3√3 см.
3.Боковая поверхность цилиндра равна 48 π см2, радиус основания – 6 см. Найдите площадь осевого сечения.
4.Площадь осевого сечения цилиндра равна 12 см2, а высота цилиндра – 2 см. Найдите радиус основания.
5. Радиусы оснований усеченного конуса равны 12 см и 6 см, а образующая наклонена к плоскости основания под углом 450. Найдите высоту конуса.
.
Вариант – 2
1. Образующая конуса наклонена к плоскости основания под углом 600 и равна 4 см. Найдите площадь осевого сечения конуса.
2.Найдите радиус шара, если расстояние от центра шара до плоскости сечения равно 3 см, а радиус сечения равен √7 см.
3.Боковая поверхность цилиндра равна 18 π см2, радиус основания – 3 см. Найдите площадь осевого сечения.
4.Площадь осевого сечения цилиндра равна 20 см2, а высота цилиндра – 5 см. Найдите радиус основания.
5. Радиусы оснований усеченного конуса равны 10 см и 4 см, а образующая наклонена к плоскости основания под углом 450. Найдите площадь осевого сечения конуса.
Время на выполнение: 45 мин.
Критерии оценивания:
За верное решение каждой из задач выставляется 1 балл.
За неверное решение задачи выставляется 0 баллов.
2.10 Контрольная работа № 2/2 по теме
«Производная функции и ее применение»
Перечень объектов контроля и оценки: У1, У3, У4, У8, У9,У10
Текст задания
Вариант – 1
1.Найдите производную функции y = x3 – 0,5 x2.
.2.Найдите y’ (1), если y = (3 – x2)(x2 + 6).
3.Материальная точка движется по закону x(t) = 3t3 – t2 + 5t (перемещение измеряется в метрах). Найдите скорость и ускорение в момент времени t = 2 с после начала движения.
4.Напишите уравнение касательной к графику функции y = 2x – x2 + 2 в точке х0 = - 1.
5. Исследуйте функцию на монотонность и найдите её наибольшее и наименьшее значения:
у = 2х3- 9х2 + 12х – 8
Вариант – 2
1.Найдите производную функции  .
.
2.Найдите y’ (- 1), если y = (3х – 7)(x3 + 2).
.
3.Материальная точка движется по закону x(t) = 2t3 – 3t2 + 5 (перемещение измеряется в метрах). Найдите скорость и ускорение в момент времени t = 2 с после начала движения.
4.Напишите уравнение касательной к графику функции y = x – 2x2 - 1 в точке х0 = 1.
5. Исследуйте функцию на монотонность и найдите её наибольшее и наименьшее значения:
у = х3 + 3х2 – 9х + 1
Время на выполнение: 45 мин.
Критерии оценивания:
За правильный ответ каждого из заданий выставляется 1 балл.
За неправильный ответ выставляется 0 баллов.
2.11Контрольная работа № 3/2 по теме «Первообразная и интеграл»
Перечень объектов контроля и оценки: У1, У3, У4, У11
Текст задания
Вариант – 1
1.Для функции у = - 3х2 + 2 найдите первообразную, график которой проходит через точку М ( 1; 5).
2.Вычислите интеграл 
3.Вычислите интеграл 
4.Найдите площадь фигуры, ограниченной линиями у = 6х, у = 0, х = 1, х = 2.
5.Найдите площадь фигуры, ограниченной графиком функции у = х2 – х, у = 0.
Вариант – 2
1.Для функции у = 3 + 4x3 найдите первообразную, график которой проходит через точку М ( 1; 1).
2.Вычислите интеграл 
3.Вычислите интеграл 
4.Найдите площадь фигуры, ограниченной линиями у = 2х, у = 0, х = 1, х = 3.
5.Найдите площадь фигуры, ограниченной графиком функции у = 3х2 – 6х , у = 0.
Время на выполнение: 45 мин.
Критерии оценивания:
За правильный ответ каждого из заданий выставляется 1 балл.
За неправильный ответ выставляется 0 баллов.
2.12Контрольная работа№ 4/2 по теме: «Измерения в геометрии».
Перечень объектов контроля и оценки: У19,У20, У22, У23, 24, У25, У26
Текст задания
Вариант 1
1.Найдите объем правильной четырехугольной пирамиды, если боковое ребро равно 3 см, а сторона основания равна 4 см.
2.Площадь осевого сечения цилиндра равна 21 см2, а площадь основания – 18 π см2. Найдите объем цилиндра.
3.Апофема правильной треугольной пирамиды равна 4см, а двугранный угол при основании равен  . Найдите объём пирамиды.
. Найдите объём пирамиды.
4. Найдите объём правильной треугольной пирамиды, высота которой равна 12см и составляет с боковым ребром угол  .
.
5.Образующая конуса равна 4 и наклонена к плоскости основания под углом 150 . Найдите объем конуса.
Вариант 2
1.Боковое ребро правильной треугольной призмы равно  см, а сторона 5 см. Найдите объём призмы
см, а сторона 5 см. Найдите объём призмы
2.Площадь осевого сечения цилиндра равна 12 см2, а площадь основания – 4 π см2. Найдите объем цилиндра.
3.Боковое ребро правильной треугольной пирамиды равно 6см и составляет с плоскостью основания угол  . Найдите объём пирамиды.
. Найдите объём пирамиды.
4.Основание прямой призмы – ромб со стороной 13см и одной из диагоналей равной 24см. Найдите объём призмы, если диагональ боковой грани 14см.
5.Образующая конуса равна 5, высота равна 4.Найдите объем конуса.
Время на выполнение: 45 мин.
Критерии оценивания:
За верное решение каждой из задач выставляется 1 балл.
За неверное решение задачи выставляется 0 баллов.
2.13Контрольная работа № 5/2 по теме: « Решение показательных и логарифмических уравнений и неравенств».
Перечень объектов контроля и оценки: У1, У2, У3, У12
Текст задания
Вариант – 1
1.Решите логарифмическое уравнение
2.Решите логарифмическое уравнение  .
.
3.Решите логарифмическое уравнение  .
.
4.Решите показательное уравнение:;
5.Решите показательное уравнение:
6.Решите показательное неравенство 
7.Решите логарифмическое неравенство log4(-x2+3x) log42.
log42.
Вариант – 2
1.Решите логарифмическое уравнение 
2.Решите логарифмическое уравнение  .
.
3.Решите логарифмическое уравнение  .
.
4.Решите показательное уравнение:
5.Решите показательное уравнение:
6.Решите показательное неравенство 
7.Решите логарифмическое неравенство log4(3x2-11x)=log4(x-12)?
Вариант – 3
1.Решите логарифмическое уравнение
2.Решите логарифмическое уравнение  .3.
.3.
3. Решите логарифмическое уравнение  .
.
4.Решите показательное уравнение:  .
.
5.Решите показательное уравнение:
6.Решите показательное неравенство 
7.Решите логарифмическое неравенство log5(x2+2x-3) .
.
Время на выполнение: 45 мин.
Критерии оценивания:
За верное решение каждого из заданий выставляется 1 балл. 7 баллов - оценка- 5; 5-6 баллов – 4; 3-4 балла - 3
2.14Контрольная работа № 6/2 по теме: «Тригонометрические уравнения».
Перечень объектов контроля и оценки: У1, У13, У14, У15
Текст задания
Вариант 1
1.Решите уравнение cos2x+1=0
2.Решите уравнение  .
.
3.Решите уравнение sin3x+sin5x=0.
4.Решите уравнение 2сos2x + 7cosx – 4 = 0
5.Решите уравнение  ;
;
6.Решите уравнение  ;
;
7.Решите уравнение ;
Вариант 2
1.Решите уравнение tg =-1
=-1
2.Решите уравнение  .
.
3.Решите уравнение cos3x+cos5x=0.
4.Решите уравнение 2sin2x + 5sinx – 3 = 0
5.Решите уравнение 2sin2x=sin2x
;
7.Решите уравнение .
.
Вариант 3
1.Решите уравнение sin2x-1=0
2.Решите уравнение  .
.
3.Решите уравнение sin3x+sinx=0.
4.Решите уравнение 3 sin2x – 5 sinx -2 =0
5.Решите уравнение cos2x=2cosx
6.Решите уравнение 3 sin2x + 10 cosx – 6 = 0.
7.Решите уравнение cosx + cos 2x = 2
Время на выполнение: 45 мин.
Критерии оценивания:
За верное решение каждого из заданий выставляется 1 балл. 7 баллов - оценка- 5; 5-6 баллов – 4; 3-4 балла – 3
2.15Итоговая контрольная работа № 2 за 2-ой курс.
Перечень объектов контроля и оценки:У1, У3, У4, У8, У9,У10,У13, У14, У15,У20, У22, У23, 24, У25, У26
Текст задания
Вариант – 1
1.Решите уравнение: соs2 х + 6 sin х – 6 =0
2. Найдите производные функций: у= 5 sin х + 3х -4
3. Решите неравенство:
4.Решите неравенство:
5.Решите уравнение: =
=  .
.
6.В прямой призме ABCА1В1С1 угол АВС - прямой, угол САВ равен 600,
AВ = 2 см, AА1 = см.
Найдите площадь полной поверхности прямой призмы.
7.Найдите высоту правильной четырёхугольной усечённой пирамиды, если стороны её основания равны 6 см и 3 см, а боковая поверхность равновелика сумме оснований.
8.Найдите площадь осевого сечения цилиндра, если диагональ осевого сечения равна 4 и образует с основанием угол 45 .
9.Найдите промежутки возрастания функции 
10. Составить уравнение касательной к графику функции  в точке х0= -1
в точке х0= -1
Вариант – 2
1.Решить уравнение:
2. Найдите производную функции: 
3.Решите неравенство: log3 (1 – x)  log3 (3 – 2x)
log3 (3 – 2x)
4.Решите уравнение 
 = х - 4.
= х - 4.
5.Решите неравенство:
6.Найти объём правильной четырёхугольной усечённой пирамиды, если боковое ребро равно 3 см, стороны основания равны 5 см и 1 см. В ответ запишите значение 3V.
7. Образующая конуса равна 5, высота равна 4. Найдите площадь (S) его поверхности.
8.Шар радиуса 13 пересечён плоскостью на расстоянии 5 от центра шара. Найдите радиус сечения
9.Найдите промежутки убывания функции 
10.Найдите наименьшее значение функции  на отрезке
на отрезке
Вариант 3
1.Решить уравнение:
2.Найдите производную функции: 
3.Решите неравенство log2 (2x- 5) ≥ log2 (x- 7)
4.
5.Решить уравнение: = 6 + х.
= 6 + х.
6.Найдите площадь боковой поверхности конуса, образующая которого равна 10, длина окружности основания равна 12.
7.Шар радиуса 13 пересечён плоскостью на расстоянии 5 от центра шара. Найдите радиус сечения.
8.Диагональ правильной четырёхугольной призмы равна 4 и наклонена к плоскости основания под углом 450 . Найдите площадь диагонального сечения.
9.Дана функция Найдите её критические точки.
Найдите её критические точки.
10.Найдите наибольшее значение функции  на отрезке
на отрезке 
Время на выполнение: 90 мин.
Критерии оценивания:
За верное решение каждого из заданий выставляется 1 балл. 9-10 баллов - оценка- 5; 7-8 баллов – 4; 5-6 баллов – 3
Разработала преподаватель математики АКХП г. Армянск Крым


 Получите свидетельство
Получите свидетельство Вход
Вход


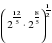
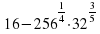
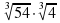 –
– 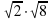
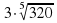 ·
· 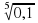
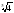 - log2 7.
- log2 7.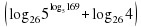 2 –
2 – 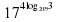
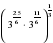 .
.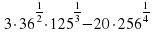
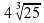 · 2
· 2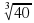
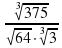
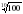 - log5 15.
- log5 15.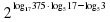
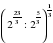 .
.








 Контрольно-измерительный материал по математике (0.22 MB)
Контрольно-измерительный материал по математике (0.22 MB)
 0
0 3598
3598 238
238 Нравится
0
Нравится
0


