Контрольно-измерительные материалы по теме
Цилиндр, конус, шар.
| Тематическое планирование |
-
| Цилиндр |
-
| Площадь поверхности цилиндра |
-
| Площадь поверхности цилиндра |
-
| Конус |
-
| Площадь поверхности конуса |
-
| Усеченный конус |
-
| Усеченный конус |
-
| Сфера и шар |
-
| Взаимное расположение сферы и плоскости |
-
| Касательная плоскость к сфере |
-
| Площадь сферы |
-
| Контрольная работа |
Уметь:
выполнять чертежи по условию задачи;
строить осевое сечение цилиндра и находить его площадь;
решать задачи на нахождения площади боковой и полной поверхности цилиндра;
выполнять построение конуса и усеченного конуса и их сечений;
находить элементы конуса и усеченного конуса;
решать задачи на нахождение площади поверхности конуса и усеченного конуса;
определять взаимное расположение сфер и плоскости;
составлять уравнение сферы по координатам точек;
уметь решать типовые задачи на нахождение площади сферы.
Знать:
формулы площадей боковой и полной поверхностей цилиндра. элементы конуса;
элементы усеченного конуса;
формулы площади боковой и полной поверхности конуса и усеченного конуса;
определение сферы и шара;
свойства касательной к сфере; уравнение сферы;
формулу площади сферы.
Тесты текущего контроля знаний и умений освоения общеобразовательной дисциплины «Математика»
Тема 3.Площадь поверхности цилиндра.
Вариант 1
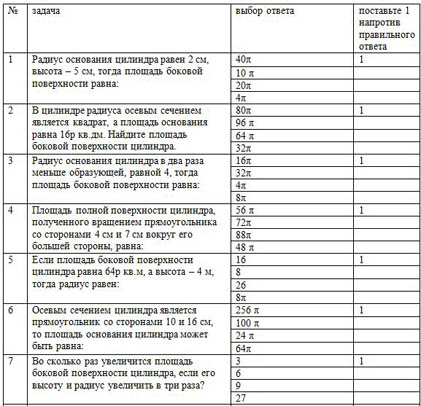
| № | задача | выбор ответа | поставьте 1 напротив правильного ответа |
| 1 | Радиус основания цилиндра равен 2 см, высота – 5 см, тогда площадь боковой поверхности равна: | 40π | 1 |
| 10 π | |
| 20π | |
| 4π | |
| 2 | В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 16p кв.дм. Найдите площадь боковой поверхности цилиндра. | 80π | 1 |
| 96 π | |
| 64 π | |
| 32π | |
| 3 | Радиус основания цилиндра в два раза меньше образующей, равной 4, тогда площадь боковой поверхности равна: | 16π | 1 |
| 32π | |
| 4π | |
| 8π | |
| 4 | Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его большей стороны, равна: | 56 π | 1 |
| 72π | |
| 88π | |
| 48 π | |
| 5 | Если площадь боковой поверхности цилиндра равна 64p кв.м, а высота – 4 м, тогда радиус равен: | 16 | 1 |
| 8 | |
| 26 | |
| 8π | |
| 6 | Осевым сечением цилиндра является прямоугольник со сторонами 10 и 16 см, то площадь основания цилиндра может быть равна: | 256 π | 1 |
| 100 π | |
| 24 π | |
| 64π | |
| 7 | Во сколько раз увеличится площадь боковой поверхности цилиндра, если его высоту и радиус увеличить в три раза? | 3 | 1 |
| 6 | |
| 9 | |
| 27 | |
| 8 | Осевым сечением цилиндра является прямоугольник со сторонами 12 и 8 см, то площадь боковой поверхности цилиндра может быть равна: | 36π | 1 |
| 64 π | |
| 48 π | |
| 96 π | |
| 9 | Во сколько раз уменьшится площадь боковой поверхности цилиндра, если его высоту уменьшить в 4 раза а радиус увеличить в 2 раза? | не изменится | 1 |
| 8 | |
| 4 | |
| 2 | |
| 10 | Во сколько раз увеличится площадь боковой поверхности цилиндра, если его высоту уменьшить в 3 раза а радиус увеличить в 12 раз? | 4 | 1 |
| 6 | |
| не изменится | |
| 8 | |
Вариант 2
| № | задача | выбор ответа | поставьте 1 напротив правильного ответа |
| 1 | Диаметр основания цилиндра равен 4 см, высота – 3 см, тогда площадь боковой поверхности равна: | 40π | |
| 10π | |
| 12π | 1 |
| 4π | |
| 2 | В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 9p кв.дм. Найдите площадь полной поверхности цилиндра. | 40π | |
| 54 π | 1 |
| 60π | |
| 32 π | |
| 3 | Радиус основания цилиндра в три раза меньше образующей, равной 6, тогда площадь боковой поверхности равна: | 24 π | 1 |
| 32π | |
| 4 π | |
| 8 π | |
| 4 | Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его меньшей стороны, равна: | 56π | |
| 10π | |
| 154π | 1 |
| 48 π | |
| 5 | Если площадь боковой поверхности цилиндра равна 64p кв.м, а радиус – 8м, тогда образующая равна: | 16 | |
| 4 | 1 |
| 26 | |
| 8 π | |
| 6 | Осевым сечением цилиндра является прямоугольник со сторонами 10 и 16 см, то площадь основания цилиндра может быть равна: | 256 π | |
| 100 π | |
| 240 π | |
| 250π | 1 |
| 7 | Во сколько раз увеличится площадь боковой поверхности цилиндра, если его радиус увеличить в три раза? | 9 | |
| не изменится | |
| 3 | 1 |
| 27 | |
| 8 | Осевым сечением цилиндра является прямоугольник со сторонами 6 и 8 см, то площадь боковой поверхности цилиндра может быть равна: | 9 π | |
| 64 π | |
| 36 π | |
| 48 π | 1 |
| 9 | Как изменится площадь боковой поверхности цилиндра, если его высоту увеличить в 4 раза, а диаметр уменьшить в 2 раза? | уменьшится в 2 раза | |
| увеличится в 4 раза | |
| не изменится | |
| увеличится в 2 раза | 1 |
| 10 | Во сколько раз увеличится площадь боковой поверхности цилиндра, если его высоту уменьшить в 3 раза, а радиус увеличить в 6 раз? | 2 | 1 |
| 6 | |
| не изменится | |
| 3 | |
Тема6. Конус. Боковая и полная поверхность конуса. Тест создан в оболочке с случайным выбором ответов
| № |
| Конус | Ответ |
| 1 | 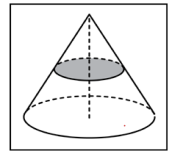
| Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. | 2 3 5 | 2 |
| 2 | 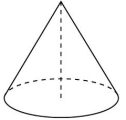
| Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на π. | 100 120 128 | 128 |
| 3 | 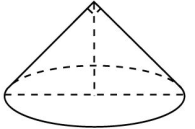
| Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на . | 4 7 9 | 9 |
| 4 | 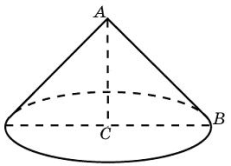
| Конус получается при вращении равнобедренного прямоугольного треугольника АВС вокруг катета, равного 6. Найдите его объем, деленный на π. | 28 58 72 | 72 |
| 5 | 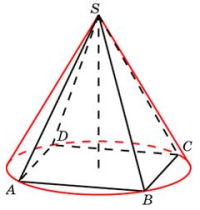
| Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на π.
| 16 18 44 | 16 |
| 6 | 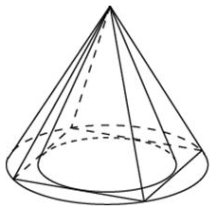
| Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду? | 2 4 6 | 2 |
| 7 | 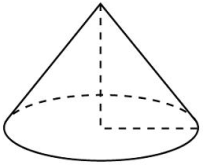
| Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса. | 2 3 4 | 3 |
| 8 | 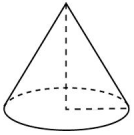
| Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза? | 3 6 9
| 3 |
| 9 | 
| Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 1,5 раза?
| 1,5 3 9 | 1,5 |
| 10 | 
| Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на π. | 100 144 244 | 144 |
| 11 | 
| Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах. | 30 45 60 | 600 |
| 12 | 
| Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса. | 3 6 8 | 3 |
| 13 | 
| Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на π. | 12 24 44 | 24 |
| 14 | 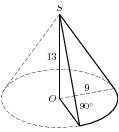 13; 9; 900 13; 9; 900
| Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/π. | 7,75 80,75 87,75 | 87,75 |
Карточки задания текущего контроля знаний и умений освоения общеобразовательной дисциплины «Математика»
Тема 3 . Площадь поверхности цилиндра.
Карточка 1 Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра. 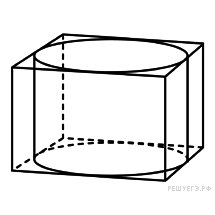
Ответ: 0,25.
Карточка 2
В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
Ответ: 3. 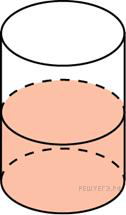 Карточка 3
Карточка 3
Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
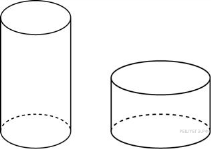
Ответ: 1,125.
Карточка 4 Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Ответ: 6.
Карточка 5 Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на  .
.
Ответ: 4.
Тема6 Конус. Боковая и полная поверхность конуса
Карточка 1
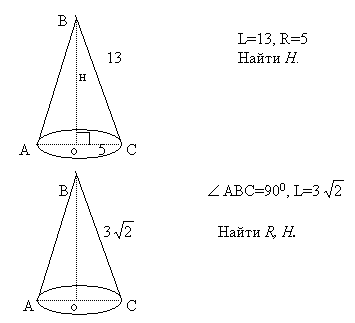
Карточка 2
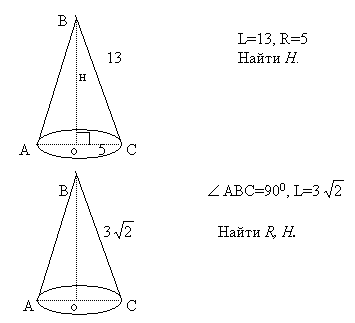
Карточка3
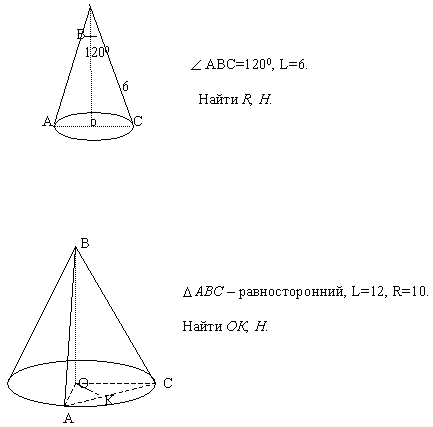
Карточка 4
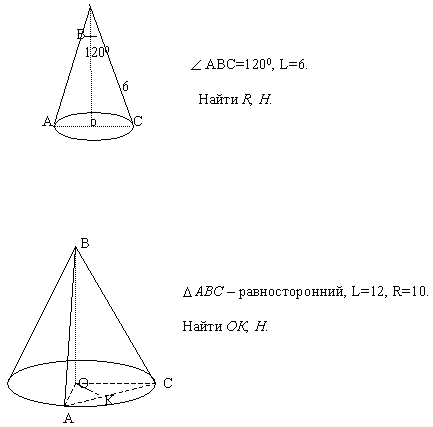 Карточка5
Карточка5
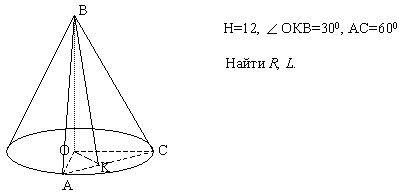
Ответы:
| | 1 | 2 | 3 | 4 | 5 |
| l | | | 2 | 2 | |
| r | 1,5 | | | 
| 3 |
| h | 1,5 | | | | |
| S | | 
| | | 9 |
Тема11 Уравнение сферы
Карточка 1
Ответить на вопрос:
Чему равен угол между плоскостью основания цилиндра и плоскостью, проходящей через образующую цилиндра?
Напишите уравнение сферы радиуса R с центром А, если: А(2,4,5), R=5
Напишите уравнение сферы с центром А, проходящей через точку , если
А(3,5,6), N(2,3,6)
Найдите площадь сферы, радиус которой равен 8см.
Карточка 2
Ответить на вопрос:
Что представляет собой сечение цилиндра плоскостью, параллельной его образующей?
Напишите уравнение сферы радиуса R с центром А, если: А(-5,-1,0), R=4
Напишите уравнение сферы с центром А, проходящей через точку , если
А(-2,4,1), N(2,-3,4)
Найдите площадь сферы, радиус которой равен 11см.
Карточка 3
Ответить на вопрос:
Равны ли друг другу углы между образующими конуса и плоскостью основания?
Напишите уравнение сферы радиуса R с центром А, если: А(-1,2,0), R=7
Напишите уравнение сферы с центром А, проходящей через точку , если
А(-4,0,1), N(2,0,-4)
Найдите площадь сферы, радиус которой равен 9см.
Карточка 4
Ответить на вопрос:
Равны ли друг другу углы между образующими конуса и его осью?
Напишите уравнение сферы радиуса R с центром А, если: А(8,-1,0), R=5
Напишите уравнение сферы с центром А, проходящей через точку , если
А(-2,3,4), N(2,0,-4)
Найдите площадь сферы, радиус которой равен 6см.
Карточка 5
Ответить на вопрос:
Что представляет собой сечение конуса плоскостью, проходящей через его вершину?
Напишите уравнение сферы радиуса R с центром А, если: А(3,-1,0), R=3
Напишите уравнение сферы с центром А, проходящей через точку , если
А(2,0,4), N(2,1,-1)
Найдите площадь сферы, радиус которой равен 2см.
Карточка 6
Ответить на вопрос:
Точки А и В принадлежат шару. Принадлежит ли этому шару любая точка отрезка АВ?
Напишите уравнение сферы радиуса R с центром А, если: А(4,4,4), R=4
Напишите уравнение сферы с центром А, проходящей через точку , если
А(-1,3,1), N(2,0,-2)
Найдите площадь сферы, радиус которой равен 1см.
Карточка 7
Ответить на вопрос:
Могут ли две сферы с общим центром и с неравными радиусами иметь общую касательную плоскость?
Напишите уравнение сферы радиуса R с центром А, если: А(1,-1,5), R=3
Напишите уравнение сферы с центром А, проходящей через точку , если
А(-2,0,0), N(2,0,-4)
Найдите площадь сферы, радиус которой равен 9см.
Карточка 8
Ответить на вопрос:
Что представляет собой множество всех точек пространства, из которых данный отрезок виден под прямым углом?
Напишите уравнение сферы радиуса R с центром А, если: А(6,-5,7), R=5
Напишите уравнение сферы с центром А, проходящей через точку , если
А(0,3,6), N(2,3,5)
Найдите площадь сферы, радиус которой равен 4см.
ОТВЕТЫ
|
| 1 вопрос | 2 вопрос | 3 вопрос | 4 вопрос |
| 1 | 900 | (x-2)2+(y-4)2+(z-5)2=25 | (x-3)2+(y-5)2+(z-6)2=5 | 256 |
| 2 | прям-к | (x+5)2+(y+1)2+z2=16 | (x+2)2+(y-5)2+(z-6)2=74 | 484 |
| 3 | да | (x+1)2+(y-2)2+z2=49 | (x+4)2+y2+(z-1)2=61 | 324 |
| 4 | да | (x-8)2+(y+1)2+ z2=25 | (x+2)2+(y-3)2+(z-4)2=89 | 144 |
| 5 | р/б треуг-к | (x-3)2+(y+1)2+z2=9 | (x-2)2+y2+(z-4)2=26 | 16 |
| 6 | да | (x-4)2+(y-4)2+(z-4)2=16 | (x+1)2+(y-3)2+(z-1)2=27 | 4 |
| 7 | нет | (x-1)2+(y+1)2+(z-5)2=9 | (x+2)2+y2+z2=20 | 324 |
| 8 | сфера диаметр | (x-6)2+(y+5)2+(z-7)2=25 | x2+(y-3)2+(z-6)2=5 | 64 |
Самостоятельная работа текущего контроля знаний и умений освоения общеобразовательной дисциплины «Математика»
Тема 7 Усеченный конус. Решение задач.
1.Найдите образующую усеченного конуса, если радиусы оснований
равны 3 см и 6 см, а высота равна 4 см.
Ответ 5см
2.Радиусы оснований усеченного конуса равны 5 см и 11 см, а образующая равна 10 см. Найдите высоту усеченного конуса?
Ответ 8 см
3.Радиусы оснований усеченного конуса равны R и r , где R r , а образующая составляет с плоскостью основания угол в 45°. Найдите площадь осевого сечения?
Ответ R² -r ²
Тема 9 Сфера и шар
1.Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Ответ: 12.
2.Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
Ответ: 12.
3.Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
Ответ: 4.
Самостоятельная работа рубежного контроля знаний и умений освоения общеобразовательной дисциплины «Математика»
Тема 16 Решение задач
Вариант 1
1. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. Ответ: 2
2. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 87. Ответ: 261
3. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 81. Ответ: 243
Вариант2
4. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 14. Ответ: 42
5.Радиус основания цилиндра 3, высота 8. Найти диагональ осевого сечения. ( Ответ: 10).
6.Осевое сечение цилиндра – квадрат, площадь которого 12. Найти площадь основания.(Ответ: 2π )
Кроссворд . (дополнительное задание на «5»)
По горизонтали:
1. Перпендикуляр, опущенный из вершины конуса на плоскость основания. 2. Плоскость, проходящая через образующую цилиндра перпендикулярно осевому сечению. 3. Сечение цилиндра плоскостью. 4. Сечение конуса плоскостью. 5. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара. 6. Тело, состоящее из всех точек пространства, находящихся на расстоянии, не большем данного от данной точки.
По вертикали:
4. Тело, состоящее из круга и точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих эту точку с точками круга. 8. Отрезок, соединяющий вершину конуса с точками окружности основания. 9. Граница шара. 10. Сечение цилиндра плоскостью, проходящей через ось цилиндра. 11. Тело, состоящее из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
ОТВЕТЫ
По горизонтали: 1. Высота. 2. Касательная. 3. Круг. 4. Круг. 5. Диаметр.
6. Шар.
По вертикали: 4. Конус. 8. Образующая. 9. Сфера. 10. Осевое. 11. Цилиндр.
Контроль по разделу знаний и умений освоения общеобразовательной дисциплины «Математика»
Контрольная работа
1. Вариант.
1. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь боковой поверхности цилиндра.
2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 60°. Найдите площадь сечения, проходящего через две образующие, угол между которыми равен 45° и площадь боковой поверхности конуса.
3. Диаметр шара равен d. Через конец диаметра проведена плоскость под углом 45° к нему. Найдите площадь сечения шара этой плоскостью.
4. В цилиндре проведена плоскость, параллельная оси и отсекающая от окружности основания дугу в 90°. Диагональ сечения равна 10 см и удалена от оси на 4 см. Найдите площадь боковой поверхности цилиндра.
5.Коническая воронка, радиус основания которой R, а высота H, наполнена водой. В воронку опущен тяжелый шар. Каким должен быть радиус шара, чтобы объем воды, вытесненный из воронки погруженной частью шара, был максимальным?
Ответы к контрольной работе
1 вариант
1. 8 см2.
2. 36 см2, 72 см2.
см2, 72 см2.
3.  см2.
см2.
4. 48 см2.
см2.
5.
2. Вариант.
1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16 π см2. Найдите площадь боковой поверхности цилиндра.
2. Высота конуса равна 6см, угол при вершине осевого сечения равен 90°. Найдите площадь сечения, проходящего через две образующие, угол между которыми равен 30° и площадь боковой поверхности конуса.
3. Площадь сечения шара плоскостью, проведенной через конец диаметра под углом 30 °к нему, равна 75π см2. Найдите диаметр шара.
4. Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 3 см, и стягивающей дугу 120°. Плоскость сечения составляет с плоскостью основания угол 45°. Найдите площадь боковой поверхности конуса.
5. В сферу вписан конус, образующая которого равна l, а угол при вершине осевого сечения равен 60 градусов. Найдите площадь сферы.
Ответы к контрольной работе
2 вариант
1. 64 см2.
2. 18 см2, 36 см2.
см2.
3. 20 см.
4. см2.
см2.
5. 4/3πl2.
Готовимся к ЕГЭ.
1. В цилиндрическом сосуде уровень жидкости достигает 48 см.
На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в см.
2. Цилиндр и конус имеют общее основание и высоту. Найдите объем цилиндра, если объем конуса равен 42.
3. Объем конуса равен 20. Через середину его высоты провели плоскость, параллельную основанию.
Найдите объём конуса, отсекаемого этой плоскостью.
4.Дано два цилиндра. Объём первого цилиндра равен 12. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра.
5. В цилиндрический сосуд налили 2200 см3. Уровень воды при этом достигает высоты 16 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 6 см. Чему равен объем детали? Ответ выразите в см3.
6. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объем параллелепипеда равен 18. Найдите высоту цилиндра.

 Получите свидетельство
Получите свидетельство Вход
Вход















 13; 9; 900
13; 9; 900
 Карточка 3
Карточка 3


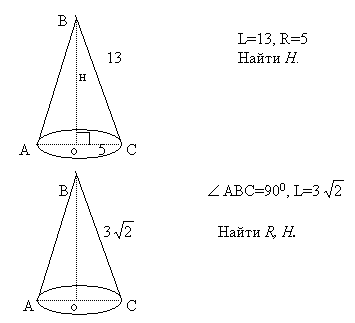
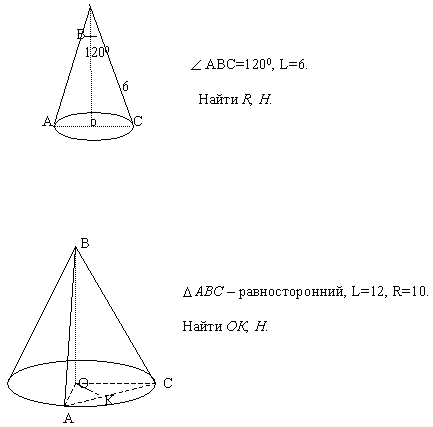










 Контрольно-измерительные материалы по математике по теме "Цилиндр, конус, шар" (0.5 MB)
Контрольно-измерительные материалы по математике по теме "Цилиндр, конус, шар" (0.5 MB)
 0
0 4746
4746 811
811 Нравится
0
Нравится
0


