Министерство образования и науки Челябинской области
государственное бюджетное профессиональное образовательное учреждение
«Южно-Уральский многопрофильный колледж»
КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ
ДЛЯ ПРОВЕДЕНИЯ РУБЕЖНОГО МОНИТОРИНГА ЗНАНИЙ
ПО ДИСЦИПЛИНЕ МАТЕМАТИКА
ДЛЯ СПЕЦИАЛЬНОСТИ 21.02.05
ЗЕМЕЛЬНО-ИМУЩЕСТВЕННЫЕ ОТНОШЕНИЯ
г. Челябинск, 2016
О Д О Б Р Е Н О
Цикловой методической комиссией
естественнонаучных дисциплин
Протокол № 5
« 26 » января 2016 г.
Председатель ЦМК
_____________О.Н. Суханова
Составитель: М.А. Вуйлова, методист, преподаватель математики высшей категории ГБПОУ «Южно-Уральский многопрофильный колледж»
Рецензент: Е.А.Кондратьева, преподаватель математики высшей категории ГБПОУ «Южно-Уральский многопрофильный колледж»
Данная методическая разработка предназначена для проведения мониторинга знаний обучающихся по основным разделам рабочей программы в форме тестирования.
Контрольно-измерительные материалы разработаны на основе рабочей программы учебной дисциплины «Математика», направлены на проверку у обучающихся усвоения знаний и сформированности умений базового уровня. Контрольно-измерительные материалы могут быть также использованы в качестве раздаточного материала, при организации самостоятельной работы студентов и на практических занятиях.
В методической разработке приведены критерии оценивания отдельных заданий.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рубежный мониторинг знаний обучающихся проводится в форме тестирования (I семестр).
Контрольно-измерительные материалы разработаны на основе рабочей программы учебной дисциплины Математика (ЕН.01) для специальности 21.02.05 Земельно-имущественные отношения.
В предъявленные контрольно-измерительные материалы включены задания, проверяющие у студентов качество усвоения знаний и сформированости умений базового уровня.
Контрольно-измерительные материалы включают в себя 4 варианта заданий (каждый вариант содержит 20 тестов), охватывающих дидактические единицы следующих разделов рабочей программы учебной дисциплины:
раздел 1. Элементы линейной алгебры;
раздел 2. Элементы аналитической геометрии;
раздел 3. Основы теории комплексных чисел.
Критерии оценивания работы
Задания 1-14 оцениваются:
Задания 15-20 оцениваются:
двумя баллами при их верном выполнении;
одним баллом, если в решении допущена одна вычислительная ошибка, не влияющая на ход решения;
нулем баллов – в остальных случаях.
| Количество баллов | Оценка |
| 0-10 11-18 19-24 25-26 | 2 3 4 5 |
I вариант
В заданиях 1-9 выберите один правильный ответ из предложенных.
Найдите матрицу 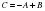 , если
, если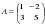 ,
, 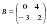 .
.
1) 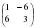 2)
2) 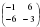 3)
3) 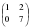 4)
4) 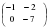
Найдите матрицу 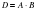 , если
, если 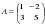 ,
, 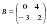 .
.
1) 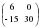 2)
2)  3)
3) 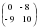 4)
4) 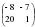
Могут ли быть равными квадратные матрицы, одна из которых третьего порядка, а другая – четвертого?
1) не могут 2) могут
Вычислите определитель матрицы 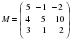 .
.
1) 60 2) 68 3) 0 4) 16
Имеет ли матрица 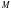 , указанная в задании №4, обратную матрицу?
, указанная в задании №4, обратную матрицу?
1) имеет 2) не имеет
Найдите алгебраическое дополнение элемента  матрицы
матрицы 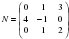 .
.
1) 1 2) 5 3) 5 4) 1
Вычислите ранг матрицы  .
.
1) 0 2) 3 3) 2 4) 1
Известно, что система линейных уравнений
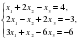
имеет единственное решение. Укажите верное утверждение:
1) данная система является определенной;
2) данная система является несовместной;
3) данная система является однородной;
4) данная система является неопределенной.
Систему линейных уравнений
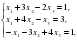
определитель  которой отличен от нуля, требуется решить с помощью формул Крамера. Укажите определитель
которой отличен от нуля, требуется решить с помощью формул Крамера. Укажите определитель 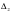 для нахождения значения переменной
для нахождения значения переменной 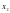 .
.
1) 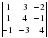 2)
2)  3)
3)  4)
4) 
Решите систему линейных уравнений методом Гаусса:

Запишите ответ.
В заданиях 11-13 выберите один правильный ответ из предложенных.
Найдите длину вектора  , если
, если  ,
,  .
.
1) 100 2) 10 3) 2 4) 14
Найдите косинус угла между векторами  и
и  .
.
1)  2)
2)  3)
3)  4)
4) 
Треугольник  задан вершинами
задан вершинами  ,
,  и
и  . Составьте уравнение стороны
. Составьте уравнение стороны  .
.
1)  2)
2)  3)
3)  4)
4) 
К заданию 14 укажите номер установленного соответствия.
|
Прямая  задана уравнением задана уравнением  . . | Уравнение прямой, проходящей через точку  перпендикулярно прямой перпендикулярно прямой  : : |
 ; ;
 ; ;
 ; ;
 . .
|
Выполните деление комплексных чисел в алгебраической форме:
 . Запишите ответ.
. Запишите ответ.
Выполните умножение комплексных чисел в тригонометрической форме:  . Запишите ответ.
. Запишите ответ.
Вычислите с помощью формулы Муавра:  . Запишите ответ в алгебраической форме.
. Запишите ответ в алгебраической форме.
Выполните деление комплексных чисел в показательной форме:  . Запишите ответ.
. Запишите ответ.
Представьте число  в показательной форме. Аргумент
в показательной форме. Аргумент  числа
числа  укажите в границах:
укажите в границах:  . Запишите ответ.
. Запишите ответ.
Вычислите все значения  . Запишите в ответе найденные значения в алгебраической форме.
. Запишите в ответе найденные значения в алгебраической форме.
II вариант
В заданиях 1-9 выберите один правильный ответ из предложенных.
Найдите матрицу  , если
, если ,
,  .
.
1)  2)
2)  3)
3)  4)
4) 
Найдите матрицу 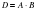 , если
, если  ,
,  .
.
1)  2)
2)  3)
3)  4)
4) 
Существует ли произведение матриц  , если матрица
, если матрица  имеет размер 3х4, а матрица
имеет размер 3х4, а матрица  – размер 2х4?
– размер 2х4?
1) существует 2) не существует
Вычислите определитель матрицы  .
.
1) 72 2) 0 3) 84 4) 12
Имеет ли матрица  , указанная в задании №4, обратную матрицу?
, указанная в задании №4, обратную матрицу?
1) не имеет 2) имеет
Найдите алгебраическое дополнение элемента  матрицы
матрицы  .
.
1) 1 2) 5 3) 1 4) 5
Вычислите ранг матрицы  .
.
1) 2 2) 0 3) 3 4) 4
Известно, что система линейных уравнений

не имеет решения. Укажите верное утверждение:
1) данная система является определенной;
2) данная система является однородной;
3) данная система является несовместной;
4) данная система является неопределенной.
Систему линейных уравнений

определитель 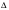 которой отличен от нуля, требуется решить с помощью формул Крамера. Укажите определитель
которой отличен от нуля, требуется решить с помощью формул Крамера. Укажите определитель  для нахождения значения переменной
для нахождения значения переменной  .
.
1)  2)
2)  3)
3)  4)
4) 
Решите систему линейных уравнений методом Гаусса:

Запишите ответ.
В заданиях 11-13 выберите один правильный ответ из предложенных.
Найдите длину вектора  , если
, если  ,
,  .
.
1) 6 2) 10 3)  4) 36
4) 36
Найдите косинус угла между векторами  и
и  .
.
1)  2)
2)  3)
3)  4)
4) 
Треугольник  задан вершинами
задан вершинами  ,
,  и
и  . Составьте уравнение стороны
. Составьте уравнение стороны  .
.
1)  2)
2)  3)
3)  4)
4) 
К заданию 14 укажите номер установленного соответствия.
|
Прямая  задана уравнением задана уравнением  . . | Уравнение прямой, проходящей через точку  параллельно прямой параллельно прямой  : : |
 ; ;
 ; ;
 ; ;
 ; ;
|
Выполните деление комплексных чисел в алгебраической форме:
 . Запишите ответ.
. Запишите ответ.
Выполните деление комплексных чисел в тригонометрической форме:  . Запишите ответ.
. Запишите ответ.
Вычислите с помощью формулы Муавра:  . Запишите ответ в алгебраической форме.
. Запишите ответ в алгебраической форме.
Выполните умножение комплексных чисел в показательной форме:  . Запишите ответ.
. Запишите ответ.
Представьте число  в показательной форме. Аргумент
в показательной форме. Аргумент  числа
числа  укажите в границах:
укажите в границах:  . Запишите ответ.
. Запишите ответ.
Вычислите все значения  . Запишите в ответе найденные значения в алгебраической форме.
. Запишите в ответе найденные значения в алгебраической форме.
III вариант
В заданиях 1-9 выберите один правильный ответ из предложенных.
Найдите матрицу  , если
, если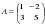 ,
, 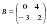 .
.
1) 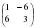 2)
2) 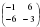 3)
3) 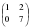 4)
4) 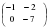
Найдите матрицу 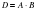 , если
, если 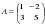 ,
, 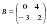 .
.
1) 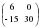 2)
2) 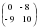 3)
3)  4)
4) 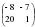
Можно ли найти сумму двух матриц, одна из которых имеет размер 3х4, а другая – размер 4х3 ?
1) можно 2) нельзя
Вычислите определитель матрицы  .
.
1) 60 2) 68 3) 16 4) 0
Имеет ли матрица 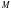 , указанная в задании №4, обратную матрицу?
, указанная в задании №4, обратную матрицу?
1) не имеет 2) имеет
Найдите алгебраическое дополнение элемента  матрицы
матрицы  .
.
1) 31 2) 25 3) 31 4) 25
Вычислите ранг матрицы  .
.
1) 0 2) 3 3) 1 4) 2
Известно, что система линейных уравнений

имеет бесконечное множество решений. Укажите верное утверждение:
1) данная система является определенной;
2) данная система является несовместной;
3) данная система является однородной;
4) данная система является неопределенной.
Систему линейных уравнений
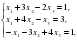
определитель 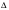 которой отличен от нуля, требуется решить с помощью формул Крамера. Укажите определитель
которой отличен от нуля, требуется решить с помощью формул Крамера. Укажите определитель  для нахождения значения переменной
для нахождения значения переменной  .
.
1) 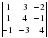 2)
2)  3)
3)  4)
4) 
Решите систему линейных уравнений методом Гаусса:

Запишите ответ.
В заданиях 11-13 выберите один правильный ответ из предложенных.
Найдите длину вектора  , если
, если  ,
,  .
.
1) 36 2) 2 3) 6 4) 10
Найдите косинус угла между векторами  и
и  .
.
1)  2)
2)  3)
3)  4)
4) 
Треугольник  задан вершинами
задан вершинами  ,
,  и
и  . Составьте уравнение стороны
. Составьте уравнение стороны  .
.
1)  2)
2)  3)
3)  4)
4) 
К заданию 14 укажите номер установленного соответствия.
|
Прямая  задана уравнением задана уравнением  . . | Уравнение прямой, проходящей через точку  перпендикулярно прямой перпендикулярно прямой  : : |
 ; ;
 ; ;
 ; ;
 . .
|
Выполните деление комплексных чисел в алгебраической форме:
 . Запишите ответ.
. Запишите ответ.
Выполните умножение комплексных чисел в тригонометрической форме:  . Запишите ответ.
. Запишите ответ.
Вычислите с помощью формулы Муавра:  . Запишите ответ в алгебраической форме.
. Запишите ответ в алгебраической форме.
Выполните деление комплексных чисел в показательной форме:  . Запишите ответ.
. Запишите ответ.
Представьте число  в показательной форме. Аргумент
в показательной форме. Аргумент  числа
числа  укажите в границах:
укажите в границах:  . Запишите ответ.
. Запишите ответ.
Вычислите все значения  . Запишите в ответе найденные значения в алгебраической форме.
. Запишите в ответе найденные значения в алгебраической форме.
IV вариант
В заданиях 1-9 выберите один правильный ответ из предложенных.
Найдите матрицу 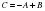 , если
, если ,
,  .
.
1)  2)
2)  3)
3)  4)
4) 
Найдите матрицу 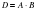 , если
, если  ,
,  .
.
1)  2)
2)  3)
3)  4)
4) 
Существует ли произведение матриц  , если матрица
, если матрица  имеет размер 3х4, а матрица
имеет размер 3х4, а матрица  – размер 4х2?
– размер 4х2?
1) существует 2) не существует
Вычислите определитель матрицы  .
.
1) 72 2) 84 3) 0 4) 12
Имеет ли матрица  , указанная в задании №4, обратную матрицу?
, указанная в задании №4, обратную матрицу?
1) имеет 2) не имеет
Найдите алгебраическое дополнение элемента  матрицы
матрицы  .
.
1) 7 2) 13 3) 7 4) 13
Вычислите ранг матрицы  .
.
1) 0 2) 2 3) 3 4) 4
Известно, что система линейных уравнений

не имеет решения. Укажите верное утверждение:
1) данная система является определенной;
2) данная система является совместной;
3) данная система является неопределенной;
4) данная система является несовместной.
Систему линейных уравнений

определитель 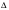 которой отличен от нуля, требуется решить с помощью формул Крамера. Укажите определитель
которой отличен от нуля, требуется решить с помощью формул Крамера. Укажите определитель 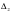 для нахождения значения переменной
для нахождения значения переменной 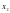 .
.
1)  2)
2)  3)
3)  4)
4) 
Решите систему линейных уравнений методом Гаусса:

Запишите ответ.
В заданиях 11-13 выберите один правильный ответ из предложенных.
Найдите длину вектора  , если
, если  ,
,  .
.
1) 14 2) 100 3) 2 4) 10
Найдите косинус угла между векторами  и
и  .
.
1)  2)
2)  3)
3)  4)
4) 
Треугольник  задан вершинами
задан вершинами  ,
,  и
и  . Составьте уравнение стороны
. Составьте уравнение стороны  .
.
1)  2)
2)  3)
3)  4)
4) 
К заданию 14 укажите номер установленного соответствия.
|
Прямая  задана уравнением задана уравнением  . . | Уравнение прямой, проходящей через точку  параллельно прямой параллельно прямой  : : |
 ; ;
 ; ;
 ; ;
 . .
|
Выполните деление комплексных чисел в алгебраической форме:
 . Запишите ответ.
. Запишите ответ.
Выполните деление комплексных чисел в тригонометрической форме:  . Запишите ответ.
. Запишите ответ.
Вычислите с помощью формулы Муавра:  . Запишите ответ в алгебраической форме.
. Запишите ответ в алгебраической форме.
Выполните умножение комплексных чисел в показательной форме:  . Запишите ответ.
. Запишите ответ.
Представьте число  в показательной форме. Аргумент
в показательной форме. Аргумент  числа
числа  укажите в границах:
укажите в границах:  . Запишите ответ.
. Запишите ответ.
Вычислите все значения  . Запишите в ответе найденные значения в алгебраической форме.
. Запишите в ответе найденные значения в алгебраической форме.
Ответы к заданиям
| № задания | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 |
| 1. | №2 | №3 | №1 | №4 |
| 2. | №2 | №4 | №3 | №1 |
| 3. | №1 | №2 | №2 | №1 |
| 4. | №3 | №2 | №4 | №3 |
| 5. | №2 | №1 | №1 | №2 |
| 6. | №4 | №3 | №2 | №1 |
| 7. | №3 | №1 | №4 | №2 |
| 8. | №1 | №3 | №4 | №4 |
| 9. | №4 | №4 | №2 | №2 |
| 10. |  |  |  |  |
| 11. | №2 | №1 | №3 | №4 |
| 12. | №4 | №3 | №1 | №2 |
| 13. | №2 | №2 | №3 | №4 |
| 14. | №3 | №4 | №3 | №1 |
| 15. |  |  |  |  |
| 16. |  |  |  |  |
| 17. |  |  |  |  |
| 18. |  |  |  |  |
| 19. |  |  |  |  |
| 20. |  |  |  |  |


 Получите свидетельство
Получите свидетельство Вход
Вход



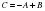 , если
, если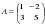 ,
, 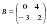 .
. 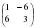 2)
2) 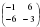 3)
3) 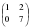 4)
4) 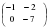
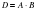 , если
, если 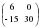 2)
2)  3)
3) 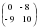 4)
4) 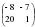
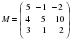 .
. 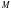 , указанная в задании №4, обратную матрицу?
, указанная в задании №4, обратную матрицу?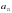 матрицы
матрицы 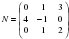 .
. .
.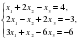
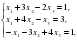
 которой отличен от нуля, требуется решить с помощью формул Крамера. Укажите определитель
которой отличен от нуля, требуется решить с помощью формул Крамера. Укажите определитель 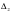 для нахождения значения переменной
для нахождения значения переменной 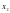 .
.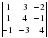 2)
2) 








 Контрольно-измерительные материалы для проведения рубежного мониторинга знаний по дисциплине "Математика" (0.33 MB)
Контрольно-измерительные материалы для проведения рубежного мониторинга знаний по дисциплине "Математика" (0.33 MB)
 0
0 520
520 39
39 Нравится
0
Нравится
0


