Конспект занятия по теме «Решение квадратных уравнений, содержащих параметр»

Данное занятие предназначено для помощи в ходе предпрофильной подготовки учащихся 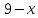классов общеобразовательной школы и входит в курс по выбору «Решение нестандартных задач с параметрами». Курс направлен на «расширение и закрепление уже полученных знаний и навыков учащихся, а так же для систематизации знаний и повышения уровня подготовки по математике через решение большого класса задач.

Тип урока: повторение, обобщение и систематизация знаний.

Цели:

Предметные: обобщение и закрепление знаний по теме «Решение квадратных уравнений с параметром».

Личностные: проявление интереса к изучению темы и повышение мотивации применять приобретённые математические знания и умения.

Метапредметные: формирование умения анализировать, сравнивать и обобщать, используя разные основания, моделировать выбор способов действий при решении поставленных задач.

Задачи:

Образовательная: обобщить и привести в систему полученные ранее знания об уравнениях с параметрами, закрепить уже существующие навыки решения уравнений;

Воспитательная: показать учащимся, что все понятия взаимосвязаны, а не изолированы друг от друга; прививать аккуратность и эстетику при оформлении записей; вырабатывать умение общаться, выслушивать других и отстаивать собственную точку зрения.

Развивающая: развивать умственную и мыслительную деятельность; умение анализировать, обобщать и выделять основное, развивать грамотную математическую речь.

Ход урока

1. Организационный этап.

2. Постановка цели урока.

Добрый день, ребята! Сегодня на уроке мы с вами обобщим и систематизируем знания по теме: “Решение квадратных уравнений, содержащих параметр”.

3. Актуализация знаний.

Устная работа.

Давайте вспомним некоторые определения:

1. Квадратное уравнение - это?

Ответ: уравнение вида 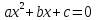, где 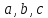— некоторые числа 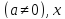– переменная.

1. Сформулируйте теорему Виета для квадратного уравнения.

Ответ: в общем случае квадратного уравнения 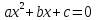теорема Виета формулируется так: если 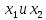– корни уравнения, то

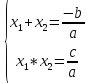
1. Что значит решить уравнение «с» параметром?

Ответ: решить уравнение с параметром – значит, для каждого значения параметра найти множество всех корней данного уравнения.

1. Какие вы знаете методы решения уравнений с параметрами?

Ответ: графический и аналитический.

5) Не решая квадратного уравнения, определите знаки его корней.

а)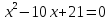

Ответ: один корень – положительный, второй – отрицательный.

б)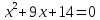

Ответ: два корня отрицательные.

в)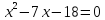

Ответ: один корень – положительный, второй – отрицательный.

г)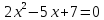

Ответ: корней нет.

4. Обобщение и систематизация знаний:

1. При каких значениях 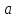корни уравнения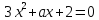

являются действительными, а сумма кубов этих корней равна их удвоенной сумме?

Решение:

Найдем значение параметров, при которых уравнение имеет действительные корни. И для этого решим неравенство :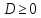

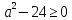
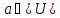
Так как согласно условию мы имеем:

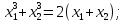
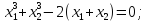
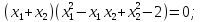
По теореме Виет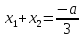а

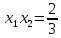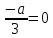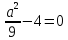
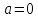, а , поэтому или

или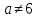

Ответ:

2) Найти все значения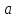, при которых один из корней уравнения в раза больше другого.

Решение: Пусть и – корни данного уравнения. Составим систему уравнений в соответствии с условием задачи:

Ответ:

5. Работа в парах

1. При каком значении сумма квадратов корней уравнения

минимальна?

1. При каких значениях оба корня уравнения

отрицательные?

6. Контроль усвоения знаний и работа над ошибками.

Найдите все значения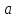, при которых уравнение

имеет два различных корня, меньших .

Решение: уравнение будет иметь два корня, когда дискриминант будет больше 0,

для того, чтобы оба корня были меньше, должно выполняться два условия:

1. абсцисса вершины параболы графика функции

должна быть меньше ;

1. значение функции в точке должно быть положительным

.

Отсюда следует, что число 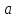удовлетворяет условиям задачи только тогда, когда 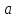удовлетворяет системе неравенств:

Ответ:

7. Рефлексия

• Что мы делали сегодня на занятии?

• Что вы узнали нового на этом занятии?

• Чем отличаются рассмотренные квадратные уравнения?

• Ребята, обратите внимание на то, что задания с параметром входят во вторую часть Единого Государственного экзамена.

8. Домашнее задание

1. Сделайте карточки для самостоятельной работы подборкой задач по данной теме .

2. Найдите все значения параметра 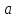, при которых для уравнения (неравенства) оба корня меньше 2:

1. Для каждого значения 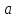решите уравнение: