Конспект урока "Закон всемирного тяготения"

Конспект урока "Закон всемирного тяготения"

Цель урока: Изучить закон всемирного тяготения, показав его практическую значимость. Более широко раскрыть понятие взаимодействия тел на примере этого закона и ознакомить учащихся с областью действия гравитационных сил.

Обучающие:

• добиться усвоения учащимися знания о законе всемирного тяготения; изучение основных законов природы;

• усвоения закона всемирного тяготения.

Развивающие:

• развивать внимание и речь;

• умение слушать и систематизировать полученные знания;

• развитие логического мышления (умение классифицировать факты, делать выводы);

• развивать речь, мышлении, совершенствовать умственную деятельность: анализ, синтез, классификация, способность наблюдать, делать выводы; выделять существенные признаки объектов, выдвигать гипотезы, проверять результаты.

Воспитывающие:

• воспитывать интерес к изучению физики;

• умение работать в совместной деятельности с преподавателем;

• коммуникативные качества личности;

• формировать систему взглядов на мир

• воспитывать интерес к творческой и исследовательской работе

Ход урока

I. Организационный момент (2 мин.)

“Я смотрю на себя, как на ребенка, который, играя на морском берегу, нашел несколько камешков поглаже и раковин попестрее, чем удавалось другим, в то время как неизмеримый океан истины расстилался перед моим взором неисследованным”

Исаак Ньютон (слайд 1)

Запишите тему урока: “Закон Всемирного тяготения” (слайд 2)

II. Актуализация знаний. Разминка (8 мин.)

Для повторения вашему вниманию предлагаются задания с выбором ответа. Повторение по теме “Второй и третий закон Ньютона”:

1. Причиной возникновения ускорения является (слайд 3)

1. Изменение скорости тела

2. Действие на тело других тел с некоторой силой

3. Изменение траектории тела

2. Второй закон Ньютона можно записать так:

3. Вектор ускорения совпадает по направлению с вектором (слайд 4)

1. Скорости

2. Перемещения

3. Равнодействующей силы

4. Третий закон Ньютона формулируется так: силы, с которыми два тела действуют друг на друга:

1. Равны по модулю и противоположны по направлению

2. Противоположны по направлению и не равны по модулю

3. Равны по модулю и имеют одинаковые направления

5. Единица измерения силы в СИ: (слайд 5)

1. Джоуль

2. Ватт

3. Ампер

4. Ньютон

6. Какая формула правильно отражает смысл третьего закона Ньютона:

1. F1 = F2

2. F1 = -F2

3. 

4. 

7. Если равнодействующая сил, приложенных к телу, не равна нулю, то тело движется (слайд 6)

1. С ускорением

2. С постоянной скоростью

3. Сначала с постоянной скоростью, а затем с ускорением

8. Силу, действующую на тело, можно вычислить по формуле:

9. В СИ единицей силы является: (слайд 7)

1. 1 кг

2. 1 Н

3. 1 м/с2

10. Математическая запись третьего закона Ньютона имеет вид:

III. Изучение нового материала. (15 мин.)

Сегодня на уроке мы с вами изучим закон всемирного тяготения, покажем его практическую значимость. Шире раскроем понятие взаимодействия тел на примере этого закона и ознакомимся с областью действия гравитационных сил.

Сегодня мы поговорим о великой силе природы – силе всемирного тяготения. Тысячелетиями сетовал человек на эту силу. Она не позволяла строить многокилометровые башни (верхние этажи своей тяжестью давили на нижние - строение разрушалось), мосты через широкие реки (чуть просчитывались инженеры – и они с грохотом обрушивались). Между тем человек и не подозревал, скольким этой силе он обязан.

Именно она собирает воды планеты, образуя моря и океаны, удерживает голубую атмосферу Земли, да и саму Землю на орбите вокруг Солнца. Не будь этой силы, Земля и другие тела нашей планетной системы – от мельчайшего астероида до гигантского Юпитера – понеслись бы в разные стороны в черное пространство Вселенной. А сама Вселенная? И она не устояла бы без силы всемирного тяготения – галактики распались бы. (слайд 8)

Человек заставил служить себе эту силу. Издавна она направляла потоки воды, на пути которых человек воздвигал плотины и ставил турбины, она совершала работу в первом паровом двигателе английского кузнеца Ньюкомена, заставляла качаться маятники часов. Человек запустил искусственный спутник Земли, и могучая сила тяготения понесла его именно по расчетному пути.

Первый вопрос нашего урока:

IV. Открытие закона всемирного тяготения

Закон всемирного тяготения был установлен И. Ньютоном путем обобщения результатов, получе6нных известными астрономами. Важную роль сыграли закономерности движения планет, обнаруженные немецким астрономом И. Кеплером (1571–1630) в результате обработки астрономических наблюдений и информации датского астронома Тихо Браге.

Ньютон открыл закон ещё в 1666 году, но сверяя свою теорию с данными опыт, он обнаружил расхождения и не стал публиковать свои результаты. Позднее выяснилось, что данные, которыми пользовался Ньютон оказались неточными. Получив в свое распоряжение новые данные , ученый убедился в том, что открытый им закон верен и что ему “...тайна мироздания, наконец, открылась ему, единственному в мире...”

Ученый установил зависимость ускорения свободного падения от расстояния.

Он заметил, что вблизи поверхности Земли, т.е. на расстоянии 6400 км от её центра это ускорение составляет 9,8 м/с2, а на расстоянии, в 60 раз большем, у Луны, это ускорение оказывается в 3600 раз меньше, чем на Земле. Но 3600 = 602. Значит, ускорение свободного падения убывает обратно пропорционально квадрату расстояния от центра Земли. Но ускорение по второму закону Ньютона пропорционально силе. Следовательно, причиной такого убывания ускорения является аналогичная зависимость от расстояния у силы тяготения.

Формулировка закона: (слайд 9)

Сила гравитационного притяжения любых частиц прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними:

где m1 – масса первого тела;

m2 – масса второго тела;

r - расстояние между телами;

G – гравитационная постоянная.

Впервые гравитационная постоянная была измерена английским физиком Г. Кавендишем (слайд 10) в 1788 г. с помощью прибора, называемого крутильными весами. Г. Кавендиш закрепил два маленьких свинцовых шара (диаметром 5 см и массой 775 г каждый) на противоположных концах двухметрового стержня. Стержень был подвешен на тонкой проволоке. Два больших свинцовых шара (20 см диаметром и 49,5 кг) близко подводились к маленьким. Силы притяжения со стороны больших шаров заставляли маленькие перемещаться, при этом проволока закручивалась. Степень закручивания была мерой силы, действующей между шарами. Эксперимент показал, что гравитационная G = 6,65 * 10-11 Н*м2/кг2.

V. Применение закона.

Приведенная формула закона всемирного тяготения применима только для точечных масс, т.е. для тел, размеры которых значительно меньше, чем расстояние между ними. Ньютону, разработавшему анализ бесконечно малых величин, удалось показать, что она применима для точечной массы и однородного шара, а также для двух однородных шаров. Тогда входящая в формулу величина R – расстояние между центрами шаров. Формула неприменима, например, для взаимодействующих бесконечного стержня и шара. В этом случае сила тяготения обратно пропорциональна расстоянию, а не квадрату расстояния. А сила притяжения между телом и бесконечной плоскостью вообще от расстояния не зависит.(Ученики записывают в тетрадь)

Формула применима для: (слайд 11)

• точечных масс;

• точечной массы и однородного шара;

• однородных шаров.

VI. Значение закона всемирного тяготения. (слайд 12)

В результате открытия Ньютона выяснилось, что множество, казалось бы, разнородных явлений: падение тел на Землю, движения Луны и Солнца, отливы и приливы и т. д. – представляет собой проявление одного и того же закона природы – закона всемирного тяготения. Этот закон вместе с законами движения Ньютона составляет основу небесной механики.

Всемирное тяготение объясняет устойчивость Солнечной системы, движения планет и других тел. Луна сохраняет свою орбиту благодаря силе притяжения Земли; Земля удерживается на своей траектории силой притяжения Солнца.

С помощью закона всемирного тяготения стало возможным вычислить массу Солнца и планет и их плотности. (слайд 13)

Закон всемирного тяготения позволяет объяснить морские приливы и отливы притяжением Луны (пояснить с помощью чертежа).

На основании закона были открыты планеты Нептун и Плутон. (слайд 14)

Пользуясь законом всемирного тяготения, точно определяют время и место солнечных и лунных затмений.

VII. Разбор одной задачи и решение учениками двух задач. (13 мин.)

Задача 1. (слайд 15)

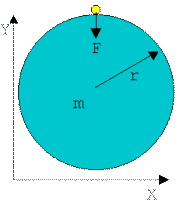
Радиус планеты в 4 раза меньше радиуса Земли, а ее масса в 80 раз меньше массы Земли. Определить ускорение свободного падения на поверхности планеты.

1. Кратко записываем условие задачи.

2, 3. Представим себе тело на поверхности этой планеты. Представим себе, что тело совершило бесконечно малое перемещение под действием силы притяжения. Изобразим условие графически, указав действующие на тело силы. Сразу обозначим на рисунке систему отсчета.

4. Записываем в векторной форме второй закон Ньютона, обозначив массу тела "m тела".

5. Записываем уравнения в проекциях на оси координат. Записываем закон всемирного тяготения. Учитываем, что проекция на ось абсцисс равна нулю, а на ось ординат - длинам векторов.

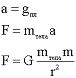
6. Решаем уравнения в общем виде.

Здесь надо сделать одно существеннейшее допущение о равенстве инертной и гравитационной масс. Ведь ниоткуда не следует, что масса тела, входящая в закон Ньютона та же самая, что и входящая в закон всемирного тяготения. Такое предположение делается.

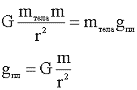
7. Подставляем величины в общее решение, вычисляем.

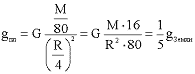
8. Ответ: ускорение свободного падения на планете в пять раз меньше, чем на Земле, что составляет примерно 2 м/с².

Задача 2. (слайд 16)

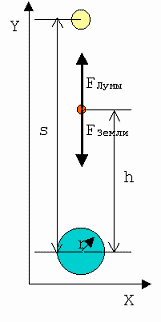
Расстояние между центрами Земли и Луны равно 6 Земным радиусам, а масса Луны в 81 раз меньше массы Земли. В какой точке отрезка, соединяющего центры Земли и Луны, тело будет в равновесии?

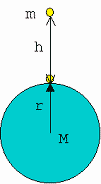
Решение.

1. Кратко записываем условие задачи.

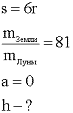
2, 3. Изображаем условие графически, указав действующие на тело силы. Сразу обозначаем на рисунке систему отсчета.

4. Записываем в векторной форме второй закон Ньютона.

5. Записываем уравнения в проекциях на оси координат.

Записываем закон всемирного тяготения.

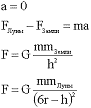
6. Решаем уравнения в общем виде.

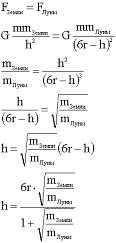
7. Подставляем величины в общее решение, вычисляем.

8. Ответ: точка равновесия находится на расстоянии 30200 км от центра Земли на прямой, соединяющей Землю и Луну.

Задача 3.

Экваториальный радиус земного шара на 21,4 км больше полюсного. Определить уменьшение ускорения свободного падения на экваторе за счет увеличения радиуса.

Решение:

,

, .

IIX. Рефлексия учебной деятельности (1 мин.) (слайд 17)

Подведение итогов.

Взаимная оценка работы на уроке.

IX. Домашнее задание (1 мин.) (слайд 18)

Параграф 15, упр.15, вопросы к параграфу № 1-7; Перышкин А.В., Гутник Е.М. Физика Дрофа 2012.

Использованные источники

1. Учебник Перышкин А.В., Гутник Е.М. Физика 9. Дрофа

2. Тематическое и поурочное планирование к учебнику А.В.Перышкина, Е.М.Гутник “Физика”, 9 класс.

3. Единая коллекция цифровых образовательных ресурсов // [Электронный ресурс]// http://school-collection.edu.ru/catalog/res/84cb4bdb-a930-4333-bf0e-bf4a6f73b640