Тема урока: «Задача о нахождении стороны квадрата».
Цели:
Образовательная: знать определение квадратного корня, учиться выполнять преобразования с квадратными корнями;
Развивающая: развивать сознательное восприятие учебного материала; познавательной активности, интереса к предмету.
Воспитательная: воспитание культуры общения; точности в записи решения примеров.
Ход урока:
Орг. момент.
Повторение изученного материала.
Устный счёт.
1. Вычислите
(-2)![]() ; 3
; 3![]() ; 0,7
; 0,7![]() ; 2
; 2![]() ; (-1)
; (-1)![]() ; (-1)
; (-1)![]()
2. . Дано: квадрат,
а) а = 6 см,
б) а = 11 см.
Найти: S. Ответ: а) 36 см2, б) 121 см2.
3. Дано: квадрат,
а) S = 25 см2,
б) S = 81 см2.
Найти: а. Ответ: а) 5 см, б) 9 см.
4. Площадь квадрата равна 49 м2. Найдите длину стороны квадрата.
(а = 7 м.).
Изучение новой темы.
Если известна длина стороны квадрата, то можно найти его площадь. В то же время приходится решать и обратную задачу – по известной площади квадрата находить его сторону.
Например, если площадь квадрата 100 см2, его сторона равна 10 см. Мы подобрали число, квадрат которого равен заданному значению площади. Таких чисел, вообще говоря, два: 10 и -10. Но мы, естественно, взяли то из них, которое является неотрицательным, - ведь отрицательным числом длина выражаться не может!
Если сторона квадрата равна a, то его площадь S можно вычислить по формуле S = a2. Но в математике есть также способ и для выражения стороны квадрата через его площадь. Чтобы записать соответствующую формулу, нам придётся ввести новый символ: 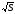 . Этим символом обозначена сторона квадрата, площадь которого равна S. Иными словами,
. Этим символом обозначена сторона квадрата, площадь которого равна S. Иными словами, 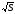 - это неотрицательное число, квадрат которого равен S. Знак
- это неотрицательное число, квадрат которого равен S. Знак 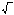 называют знаком квадратного корня или радикалом (от латинского слова radix – корень), а читают выражение
называют знаком квадратного корня или радикалом (от латинского слова radix – корень), а читают выражение 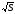 так: квадратный корень из S.
так: квадратный корень из S.
С использованием введённого символа формула для нахождения стороны квадрата a, площадь которого равна S? Запишется следующим образом:
a = 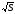 .
.
Пусть, например, S = 64. Тогда a = 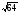 . Так как 64 = 82, то
. Так как 64 = 82, то 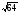 = 8. Мы заменили выражение
= 8. Мы заменили выражение 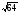 его значением – числом 8, или, как говорят, извлекли квадратный корень из 64.
его значением – числом 8, или, как говорят, извлекли квадратный корень из 64.
В приведённом примере нам нетрудно было найти значение корня. Однако если подкоренное число большое, то для извлечения корня приходиться пользоваться вспомогательными приёмами.
Пример 1. Найдём 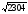 .
.
Чтобы подобрать число, квадрат которого равен 2304, обратимся к таблице квадратов двузначных чисел (см. стр. 254). Из таблицы видно, что 2304 = 482. Значит, 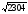 =
= 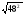 = 48.
= 48.
Пример 2. Найдём 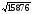 .
.
Так как под корнем пятизначное число, то таблица квадратов двузначных чисел нам уже не поможет. Поэтому воспользуемся другим приёмом – разложим число 15876 на множители.
Так как 15876 = 22  34
34  72 = (2
72 = (2  9
9  7)2, то
7)2, то 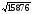 =
= 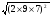 = 2
= 2  9
9  7 = 126.
7 = 126.
При записи выражений, содержащих радикалы, так же как и других алгебраических выражений, нужно придерживаться некоторых правил. Так числовой или буквенный множитель пишут перед радикалом, например 2, a
.
Знак корня, как и скобки, является группирующим символом. Если, например, нужно найти значение выражения , то сначала надо вычислить сумму 42 +32, а затем извлечь корень:
=
=
= 5.
Закрепление.
Фронтальный опрос.
Запишите формулу для нахождения стороны квадрата a по его площади S. (a =
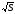 ).
).Что обозначают символом
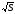 ? (Этим символом обозначена сторона квадрата, площадь которого равна S).
? (Этим символом обозначена сторона квадрата, площадь которого равна S).Найдите
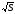 , если S = 25; 36; 0,01. (5; 6; 0,1).
, если S = 25; 36; 0,01. (5; 6; 0,1).
Решение задач.
№ 217 Вычислите:
б) = 6.
з) = 0,7.
№ 218 Вычислите:
а) =
.
е) =
.
№ 219 Вычислите, пользуясь таблицей квадратов двузначных чисел:
д) = 32.
з) =
.
Самостоятельная работа.
Три уровня сложности по возрастающей – на выбор учащегося.
1 вариант
| х | 25 | 0,36 | | 0,0001 | -16 | 2+ | 256 | |
| |
|
|
|
|
|
|
|
|
2 вариант
| а | 3 | 9 | -7 | 36 | -13 | -11 | 2 | |
| в | 6 | 16 | 11 | 64 | -12 | 11 | | |
| |
|
|
|
|
|
|
|
|
3 вариант
| а | 4 | 0 | 5 | 10 | 12 | | |
| в | 0 | -6 | -12 | 24 | 9 | 2 | -6 |
| |
|
|
|
|
|
|
|
№ 1. Выполнение теста:
Запишите значение при а, равном
а) а = 1
1) 0,1 2) -1 3) 1 4) 10.
б) а = 144
1) 144 2) 14 3) 12 4) 21.
в) а = 0,04
1) 0,4 2) 2 3) 0,2 4) 4.
Ответы: а ) 3); б) 3); в) 3)
№ 220 Найдите значение выражения при заданных значениях переменной:
б) x = ;
;
. (
;
;
).
№ 221 Верно ли, что:
б) = 0,18. (Да).
г) = 0,31. (Нет).
№ 222 Запишите равенство, связывающие данные числа, не используя знак 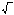 :
:
г) = 0,21. (0,0441 = 0,212).
№ 223 Запишите соотношение, между данными числами с помощью знака 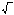 :
:
б) 412 = 1681. (41 =).
№ 224 Вычислите:
г) = 12,56.
№ 225 Вычислите:
г) = 1600.
Вычислите устно: (Физминутка)
а)= б)
в)
= д)
= к)
= л)
= м)
+
=
Подведение итогов.
РЕФЛЕКСИЯ.
Продолжите предложения:
Сегодня на уроке математики я…»
«Мне было не сложно выполнять задания, потому что…».
« Вам было не сложно выполнять задания, потому, что вы имеете хорошие знания по данной теме».
Домашнее задание: п. 2.1; стр. 55 – 56; №№. 217 – 225 (все под (в)).

 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект урока "Задача о нахождении стороны квадрата" (88.17 KB)
Конспект урока "Задача о нахождении стороны квадрата" (88.17 KB)
 0
0 522
522 59
59 Нравится
0
Нравится
0


