Тема урока: Сумма углов треугольника.
Коркина Л.Ю., учитель математики,
высшей квалификационной категории
КГУ « Средняя школа № 32»
г. Петропавловск, Северо –Казахстанская область.
Цель урока: обобщение и систематизация знаний по теме, формирование речевых, интеллектуальных и практических умений школьников
Задачи урока:
осмысление изученного материала, воспроизведение и применение знаний с целью их углубления;
развитие наблюдательности, логического мышления, развитие грамотной речи;
воспитание аккуратности, умения слушать и умения отстаивать свое мнение.
Тип урока: урок комплексного применения знаний, умений и навыков.
Оборудование: карточки-задания, мультимедийная доска.
План урока:
1. Организационный момент.
2. Устное решение задач по готовым чертежам.
3. Повторение теории.
4. Решение задач.
5. Итог урока.
6. Домашнее задание.
Ход урока:
1. Организационный момент.
Сегодня на уроке мы будем применять теоретические знания к решению задач. Решение задач – практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь. «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их», – говорил выдающийся математик Д.Пойа.
2. Устное решение задач по готовым чертежам.
В геометрии очень важно уметь смотреть и видеть, замечать и отличать различные особенности геометрических фигур.
Кто ничего не замечает,
Тот ничего не изучает,
Кто ничего не изучает,
Тот вечно хнычет и скучает.
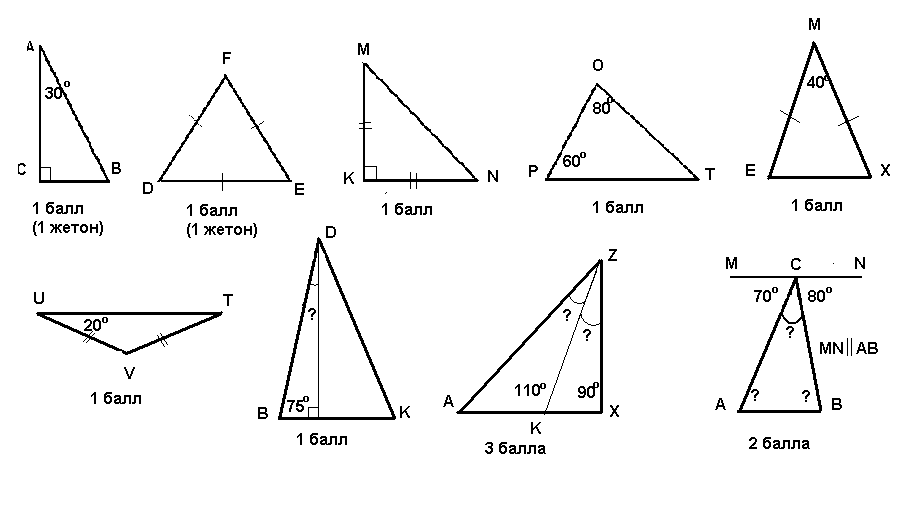
Внимательно посмотрите на рисунки и вычислите неизвестные углы треугольника (слайды).
Сформулируйте теорему, которую применяли, решая предложенные задачи.
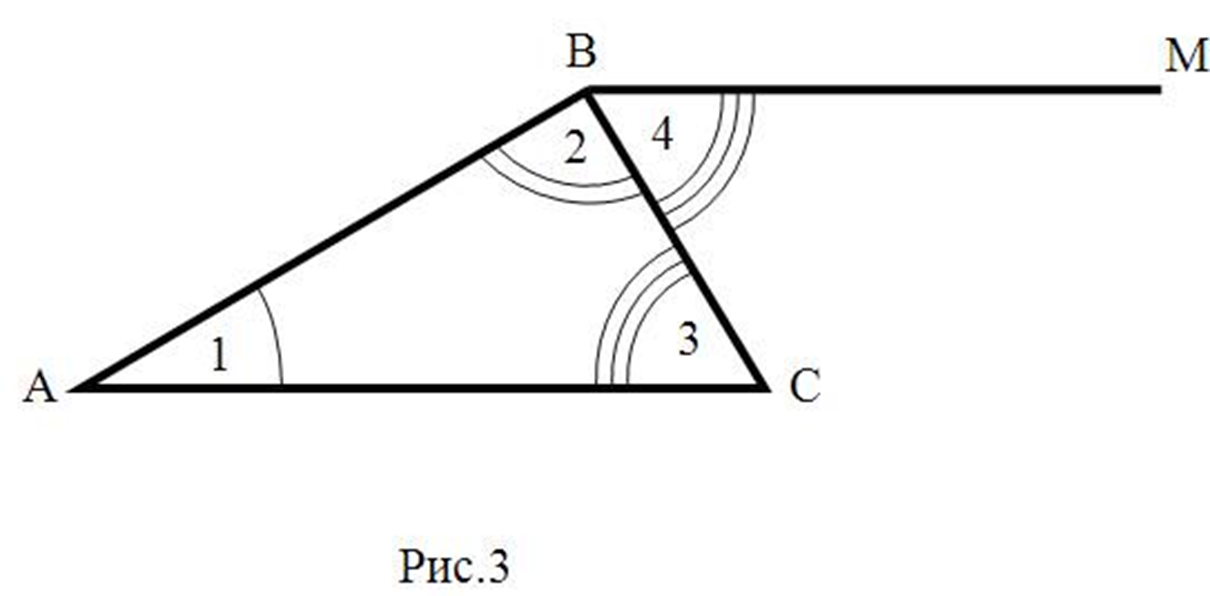
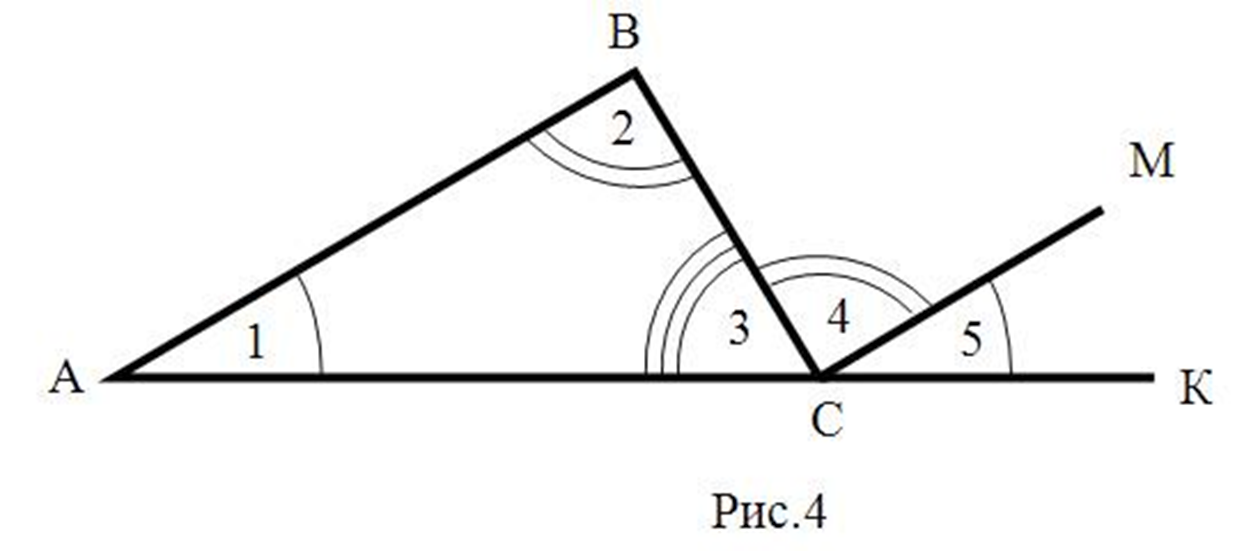
Дано: ∆ ABC
Доказать: А + В + С = 180°.
Доказательство:
Рассмотреть 4 способа доказательства (дети доказывают самостоятельно)(слайды)
|
|
|
|
|
|
3. Повторение теории (работа по карточкам)
Вариант 1
Закончи предложение:
Сумма углов треугольника равна _______
Если углы равнобедренного треугольника при основании равны 50°, то угол между боковыми сторонами равен _______
Каждый угол равностороннего треугольника равен _______
Внешним углом треугольника при данной вершине называется __________
С
 умма внешнего и внутреннего углов треугольника при данной вершине равна _______
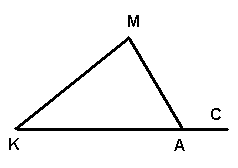
умма внешнего и внутреннего углов треугольника при данной вершине равна _______В ∆КМА внешним является угол _________
Если два внешних угла ∆АВС равны 100о и 140о, то третий внешний угол равен _______
Вариант 2
Закончи предложение:
Если в ∆АВС А = 35°, B = 55°, то С = _______
Если угол между боковыми сторонами равнобедренного треугольника равен 100°, то углы при основании равны _______
Если сумма двух углов треугольника равна третьему углу, то этот треугольник является ____________________ (вид треугольника).
При данной вершине можно построить _______ внешних угла.
В
 нешний угол треугольника равен ____________
нешний угол треугольника равен ____________В ∆КМА МАС – ______________
Сумма углов треугольника равна _______
После выполнения работы учащиеся меняются карточками. Проговариваются ответы. (слайд) Верно выполненные задания отмечаются знаком «+» и оцениваются в 1 балл. Подсчитывается сумма баллов, и по таблице, записанной на доске, выставляются соответствующие оценки. Пример таблицы:
| 10 баллов и более | «5» |
| 8 – 9 баллов | «4» |
| 6 – 7 баллов | «3» |
Решение задач.
По данным в карточках составить задачу и решить письменно. Рассмотреть все возможные случаи (слайды)
| Дан равнобедренный треугольник
| внешний угол |
| угол при основании
| угол между боковыми сторонами |
| равен 130°
| Найдите неизвестные углы треугольника. |
5. Итог урока.
Ответить на вопросы:
Сформулируйте теорему о сумме углов треугольника.
Какой треугольник называется остроугольным? Тупоугольным? Прямоугольным?
Какой угол называется внешним углом треугольника?
Каким свойством обладает внешний угол треугольника?
Учащиеся получают оценку: за работу по карточкам, устную работу, доказательство теоремы и решение задач (таблица «Критерии оценок» расположена выше).
6. Домашнее задание:
1. Подготовиться к самостоятельной работе;
2. §12 вопросы стр. 49; № 150, 162;
Индивидуальное задание «Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника, противолежащей основанию, параллельна основанию».
5

 Получите свидетельство
Получите свидетельство Вход
Вход











 Конспект урока "Сумма углов треугольника" (837.5 KB)
Конспект урока "Сумма углов треугольника" (837.5 KB)
 0
0 1514
1514 121
121 Нравится
0
Нравится
0







