Тема. Система отсчёта. Перемещение и описание движения. Графическое представление прямолинейного равномерного движения.
Цели урока: вспомнить, что такое механическое движение, материальная точка, траектория, путь, перемещение; сформировать понятие о системе отсчёта, координатах тела, их изменении, перемещении как векторе, изучить законы движения в векторном виде; сформировать понятие проекции точки и вектора на оси координат; рассмотреть графическое представление прямолинейного равномерного движения; формировать навыки построения вектора перемещения и его проекций на оси координат; развивать логическое мышление учащихся, их память, речь, внимание; воспитывать трудолюбие, добросовестность, аккуратность, самодисциплину.
Тип урока: комбинированный.
Ход урока.
Организационный момент. Постановка темы урока.
Мотивация учебной деятельности.
Сегодня мы начинаем изучение одного из разделов механики, который называется кинематикой.
Кинематика – раздел механики, изучающий движение тел, зависимость от времени величин, характеризующих движение и взаимосвязь между ними (без исследования причин движения).
Основные задачи кинематики:
Найти, какой путь прошло тело за данный интервал времени;
Рассчитать, где находится тело в данный момент времени.
Для того, чтобы решать задачи кинематики, мы должны повторить основные понятия механики, изученные ранее.
Повторение ранее изученного материала.
Вопросы учащимся:
Что называют механическим движением?
Виды механического движения.
Какое движение называют равномерным?
Что такое траектория? Виды траектории.
Что такое путь?
Что называют скоростью равномерного прямолинейного движения?
Что такое перемещение? Чем перемещение отличается от пути?
Что называют материальной точкой?
Изложение нового материала.
Траектория движения указывает все положения, которые занимала точка, но, зная траекторию, ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки траектории. Чтобы получить полное описание движения, нужно знать, в какой момент точка занимала то или иное положение на траектории. Описать движение можно:
с помощью таблиц;
графически;
аналитически (с помощью формул).
Положение материальной точки в пространстве и в произвольный момент времени можно определить, если ввести систему отсчета.
Тело отсчёта, система координат, связанная с ним, и прибор для измерения времени образуют систему отсчёта.
Системы отсчёта бывают:
Одномерные (движение автомобиля по прямой линии) – числовая прямая – положение тела задаётся одной координатой
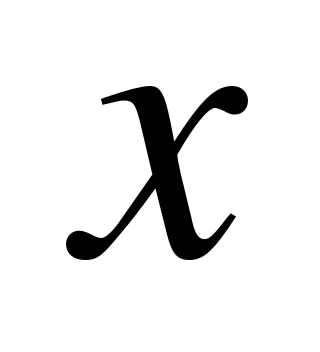 или
или  ;
;Двухмерные (движение шахматной фигуры в плоскости) – декартова система координат – положение тела задаётся на плоскости двумя координатами (
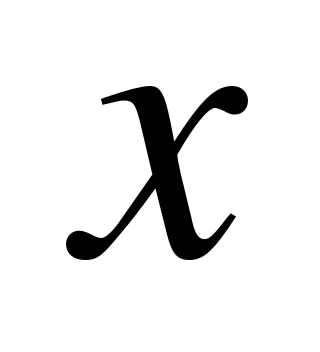 ;
; );
);Трехмерные (полет мухи в пространстве) – положение тела задаётся тремя координатами (
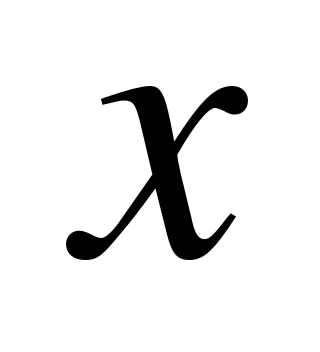 ;
; ; z).
; z).
Итак, положение точки на линии, плоскости и в пространстве определяют соответственно одним, двумя или тремя числами – координатами.
Для характеристики движения тела в выбранной системе отсчёта необходимо знать, как во времени изменяются координаты тела.


t = 0 х0, у0, z0 ∆х = х – х0
t х, у, z ∆у = у – у0 изменение
∆z = z – z0 координат
Движущееся тело изменяет своё положение в системе с течением времени, поэтому изменяются его координаты. Зная последовательность координат, мы можем зарисовать линию, по которой двигалось тело (траекторию движения).
Пример: Тело переместилось из т. А (3; -1) в т. В (5; 2), а затем в т. С (-1; 6). (изобразить на доске!)
З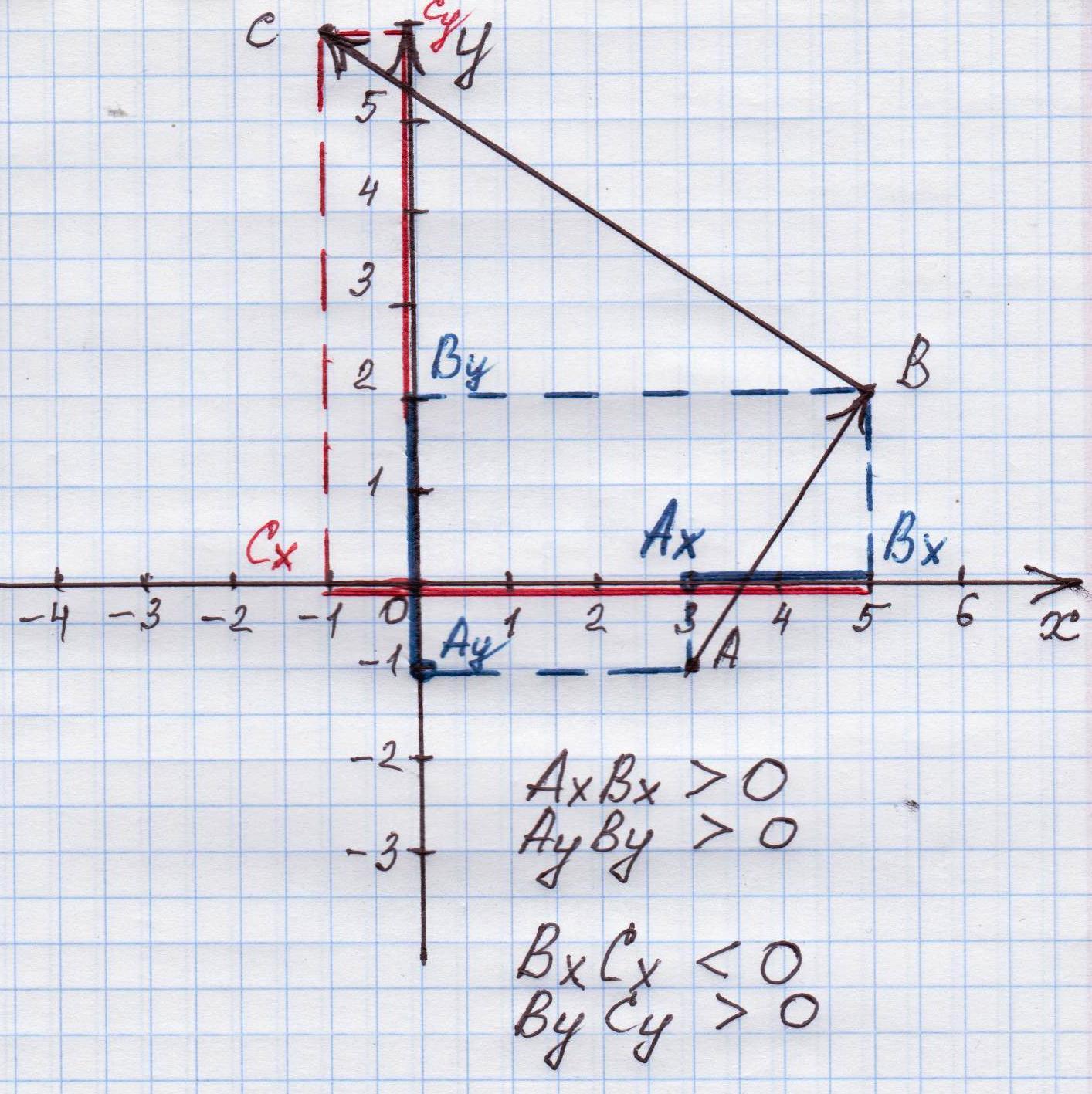 нание вектора перемещения позволяет находить положение тела в любой момент времени с помощью вычислений. Для этого познакомимся с понятием проекции вектора.
нание вектора перемещения позволяет находить положение тела в любой момент времени с помощью вычислений. Для этого познакомимся с понятием проекции вектора.
Точки Ах, Вх, – проекции точек А и В на ось Х
АхВх – проекция перемещения АВ на ось Х
Точки Ау, Ву – проекции точек А и В на ось У
АуВу – проекция перемещения АВ на ось у
Проекцию считают положительной, если от проекции начала к проекции конца вектора нужно идти по направлению самой оси. В противном случае, проекция вектора отрицательна (показать на рисунке).
Е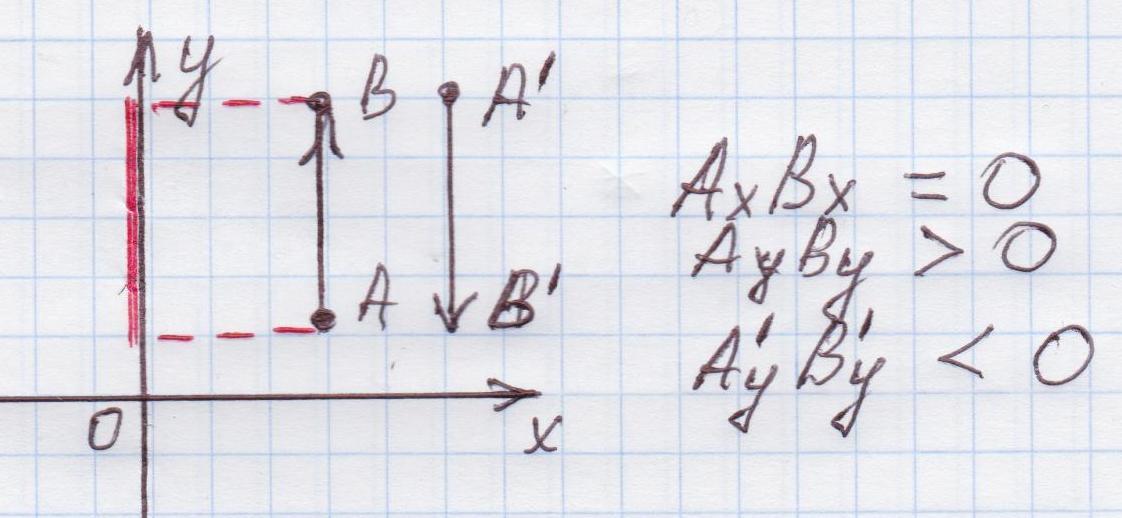 сли вектор перпендикулярен оси, то при любом направлении вектора его проекция на ось равна нулю. Если вектор параллелен оси, то модуль его проекции равен модулю самого вектора.
сли вектор перпендикулярен оси, то при любом направлении вектора его проекция на ось равна нулю. Если вектор параллелен оси, то модуль его проекции равен модулю самого вектора.
Если известна начальная координата тела и его перемещение, то можно определить конечную координату:
X = X0 + Sx ![]() Sx = X – X0
Sx = X – X0
Y = Y0 + Sy ![]() Sy = Y - Y0
Sy = Y - Y0
АхВх = ХВ – ХА = 5 – 3 = 2
АуВу = УВ – УА = 2 – (-1) = 3
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением.
Скоростью равномерного прямолинейного движения называют постоянную векторную величину, равную отношению перемещения тела за любой промежуток времени к значению этого промежутка.
![]()
![]()
![]()
Направлен вектор скорости так же, как вектор перемещения. Направление вектора скорости – это и есть направление движения тела.
При вычислениях перемещения и скорости пользуются формулами, в которые входят не векторы, а их проекции на оси координат.
s
 x = vx t x – x0 = vx t x = x0 + vxt
x = vx t x – x0 = vx t x = x0 + vxt
sx = x – x0
зависимость координаты от времени
(кинематическое уравнение движения)
Физический смысл скорости: проекция скорости на координатную ось равна изменению координаты в единицу времени, т.е скорость показывает, как быстро изменяются при движении координаты тела.
![]()
При этом проекция скорости может быть как положительной, так и отрицательной.
Формула x = x0 + vxt показывает, как с течением времени изменяется координата тела при прямолинейном равномерном движении, то есть описывает движение. Но описать движение тела можно и с помощью графика.
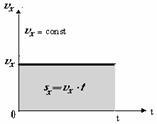
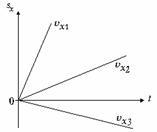
| Графическое представление равномерного прямолинейного движения | |
| 1. График зависимости проекции скорости от времени Площадь под графиком скорости численно равна перемещению. |
|
| 2. График зависимости проекции перемещения от времени Чем круче график, тем больше скорость тела. |
|
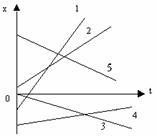
| 3. График зависимости координаты от времени. 1, 2, 4 - движение сонаправлено с осью, 3, 5 - движение против оси. |
|
Закрепление изученного материала.
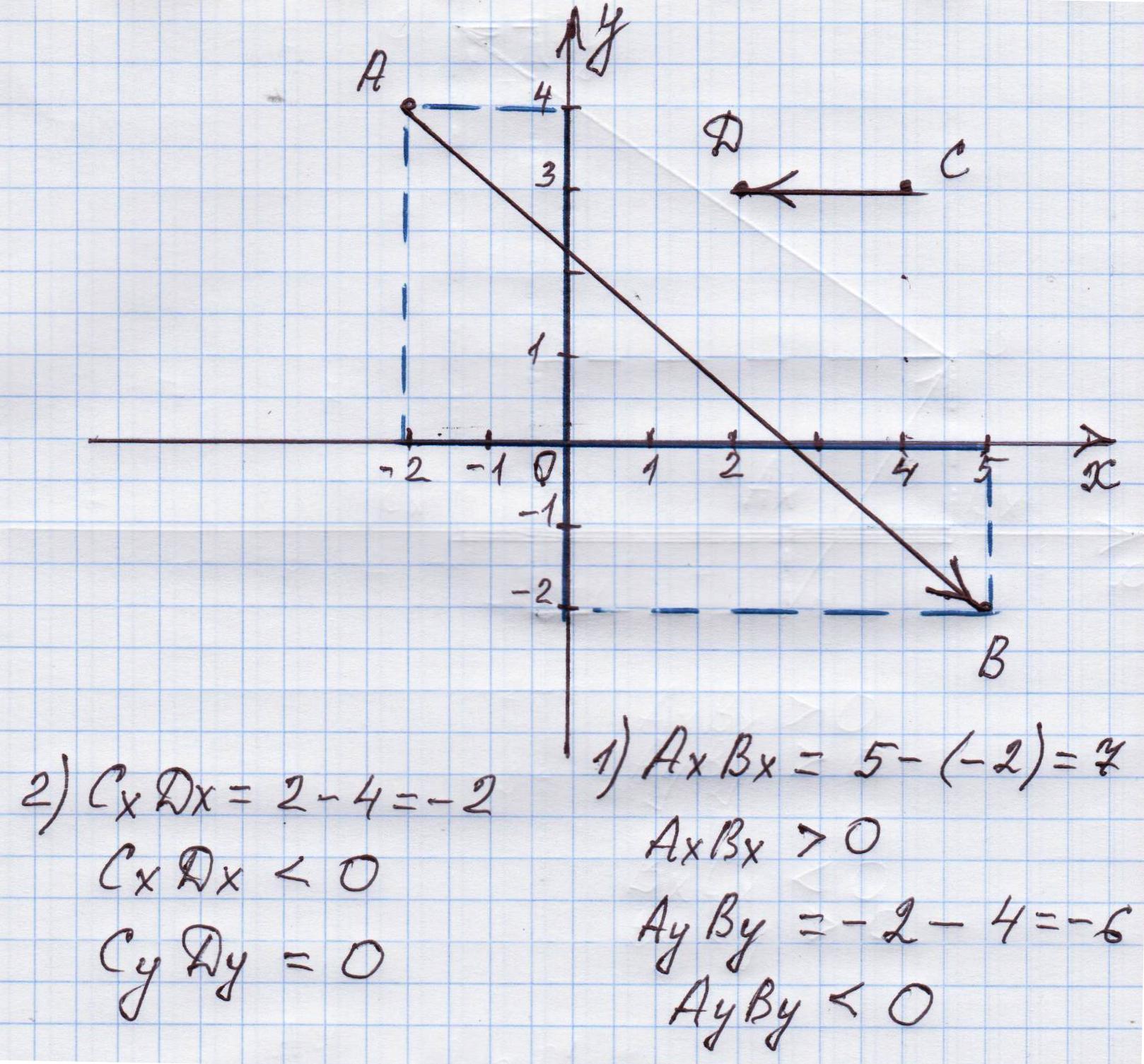
Задание 1. Построить в декартовой системе координат векторы перемещения тел и их проекции на оси координат. Определить проекции перемещений на оси координат.
1) А(-2; 4), В (5; -2);
2) С (4; 3); D (2; 3)
Задание 2. Сборник задач (Рымкевич), упр. 9
Дано:
H = 3 м Решение
h = 1 м
s = H + h
s - ? r - ? s = 3 м + 1 м = 4 м
r = H – h
r = 3м – 1м = 2м
Ответ: 4м; 2м.
Подведение итогов урока.
Домашнее задание: Белага (8)
Рымкевич упр. 11, упр. 14.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект урока "Система отсчёта, перемещение и описание движения" (689.5 KB)
Конспект урока "Система отсчёта, перемещение и описание движения" (689.5 KB)
 0
0 3149
3149 250
250 Нравится
0
Нравится
0


