18
Тема урока: «Преобразования, влияющие на изменение корней логарифмического уравнения»
Цель урока: продолжить изучение способов решения логарифмических уравнений, уделяя внимание характеристике преобразований, приводящих к нахождению корней
Задачи урока:
Учить анализировать процесс решения логарифмических уравнений и обосновать цепочку переходов от исходного уравнения равносильному или уравнению – следствию;
Формировать умение преобразовывать уравнение в равносильное или в уравнение-следствие;
Развивать логическое мышление через приемы сравнения, умение классифицировать, акцентировать внимание на постановку вопроса в задании;
Воспитывать ответственное отношение к учебе создать условия для развития коммуникативных умений, навыков совместной деятельности
Воспитывать уверенности в собственных силах
Ход урока
Организационный момент
Актуализация знаний
Формулировка темы. Постановка цели урока.
Изучение нового материала
Закрепление изученного в процессе решения задач ЕГЭ
Подведение итогов урока, рефлексия
Домашнее задание
Организационный момент
Актуализация знаний
Что мы с вами изучали на предыдущем уроке?
Что такое уравнение?
Что значит решить уравнение?
Что представляет собой процесс решения уравнения?
(Выполнение преобразований, приводящих данное уравнение к уравнению более простого вида, т.е. такого уравнения, нахождение корней которого не представляется трудным)
Что называется ОДЗ уравнения?
(Множество всех чисел, при которых имеют одновременно смысл функции, стоящие в левой и правой частях уравнения)
Какие уравнениях называются равносильными?
(Два уравнения с одной переменной f(x)=g(x) и p(x)=h(x) называются равносильными, если множества их корней совпадают)
Какие теоремы о равносильности мы изучали на предыдущем уроке?
Теорема 1. Если какой либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному.
Теорема 2. Если обе части уравнения возвести в одну и ту же нечетную степень, то получится уравнение, равносильное данному.
Теорема 3. Показательное уравнение а f(x) =а g(x) ( где а0, а≠1) равносильно уравнению f(x)=g(x).
Теорема 4. Если обе части уравнения f(x)=g(x) умножить на одно и то же выражение h(x), которое:
А) имеет смысл всюду в области определения (в ОДЗ) уравнения f(x)=g(x)
Б) нигде в этой области не обращается в 0 –
то получится уравнение f(x) h(x)=g(x) h(x), равносильное данному.
Следствие («спокойное» утверждение): Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Теорема 5. Если обе части уравнения f(x)=g(x) неотрицательны в области определения уравнения, то после возведения обеих его частей в одну и ту же четную степень n получится уравнение, равносильное данному f(x) n =g(x) n.
Теорема 6. Если f(x) 0 и g(x) 0, то логарифмическое уравнение logаf(x)= logа g(x), где а0, а≠1, равносильно уравнению f(x)=g(x).
Влияет ли переход от данного уравнения к равносильному на множество корней уравнения?
(нет, не влияет)
Всегда ли при решении уравнения мы можем перейти к равносильному уравнению?
Какие уравнения называются уравнениями – следствиями?
(Если все корни первого уравнения, являются корнями второго уравнения, то второе уравнение называется следствием первого).
Т.е. Если при переходе от одного уравнения к другому множество корней расширилось, но потери корней не произошло, то второе уравнение называется уравнением – следствием.
- Что может произойти с корнями уравнения, если решая уравнение мы изменяем ОДЗ?
(потеря корней или приобретение посторонних корней).
Как можно избавиться от посторонних корней?
(Сделать проверку).
Допустима ли потеря корней? Почему?
(Нет, т.к. решить уравнение – это найти все его корни).
Целеполагание.
Какие виды уравнений вы знаете?
Рациональные (линейные, квадратные, целые – рациональные, дробные рациональные);иррациональные, тригонометрические, логарифмические, показательные, смешанные
При решении каких уравнений часто происходит потеря корней или приобретаются новые корни?
(При решении логарифмических уравнений и иррациональных)
На дом вам было дано задание: Сравнить ОДЗ уравнений.
Уравнение (2) было получено из уравнения (1) с помощью каких – либо преобразований.
Что происходило с ОДЗ уравнений при таких преобразованиях?
(меняется)
На что это может повлиять?
Какова же тема урока?
«Преобразования, влияющие на изменение корней логарифмического уравнения»
Проблема: При решении логарифмических уравнений могут появиться посторонние корни или произойти потеря корней. Как этого избежать?
Какова цель урока?
Цель: Узнать какие преобразования могут изменить корни логарифмического уравнения
Задачи:
Выяснить:
- какие преобразования могут привести к потере корней и к появлению посторонних корней при решении логарифмического уравнения;
- как можно избежать потери корней при решении логарифмического уравнения
Изучение нового материала
Сегодня на уроке мы рассмотрим какие преобразования могут привести к потере корней и к появлению посторонних корней логарифмического уравнения.
Какое уравнение называется логарифмическим?
Определение: Логарифмическим уравнением называется уравнение, содержащее неизвестное под знаком логарифма.
Какие вы знаете методы решения логарифмических уравнений:
Решение уравнений на основании определения логарифма.
Метод введения новых переменных
Метод потенцирования
Метод логарифмирования
Приведение логарифмов к одному основанию
Применение свойств логарифма.
Функционально – графические методы решения уравнений
Работа в парах
Проверка домашнего задания.
Задание: Заполните таблицу. Что произойдет с ОДЗ уравнения (1) при переходе к уравнению (2)?
Задание: Найдите область допустимых значений каждого уравнения.
Какие преобразования выполнены при переходе от уравнения (1) к уравнению (2)
|
| (1) | ОДЗ (1) | (2) | ОДЗ (2) | Что произошло с естественной областью определения уравнения | |
| Расширилась | Сузилась | |||||
| 1 |
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
| 7 |
|
|
|
|
|
|
| 8 |
|
|
|
|
|
|
| 9 |
|
|
|
|
|
|
| 10 |
|
|
|
|
|
|
| 11 |
|
|
|
|
|
|
| 12 |
|
|
|
|
|
|
| 13 |
|
|
|
|
|
|
| 14 |
|
|
|
|
|
|
| 15 |
|
|
|
|
|
|
| 16 |
|
|
|
|
|
|
Преобразования, которые могут привести к потере корней и к появлению посторонних корней логарифмического уравнения:
Применение формул перехода к новому основанию логарифма;
Взаимное «уничтожении» подобных членов, содержащих переменную;
Формальное применение логарифмических формул (свойств логарифмов);
Освобождение в процессе решения уравнения от знаменателей, содержащих переменную величину;
При потенцировании логарифмического уравнения (освобождение в процессе решения от знаков логарифмов)
Преобразования на основе определения логарифма, если в основании переменная
Деление обеих частей уравнения на одно и то же выражение с переменной (кроме тех случаев, когда точно известно, что всюду в области определения уравнения это выражение не равно нулю)
Работа в парах по рядам
Задание: Определите, какие из этих преобразований могут привести к потере корней, а какие к появлению посторонних корней логарифмического уравнения.
Вариант1: Определите, какие из перечисленных преобразований могут привести к потере корней
Вариант 2: Определите, какие из перечисленных преобразований могут привести к появлению посторонних корней логарифмического уравнения.
| № | Преобразования | Появление посторонних корней | Потеря корней |
| 1 | Применение формул перехода к новому основанию логарифма |
| + |
| 2 | Взаимное «уничтожении» подобных членов, содержащих переменную |
| + |
| 3 | Формальное применение логарифмических формул (свойств логарифмов) | + | + |
| 4 | Освобождение в процессе решения уравнения от знаменателей, содержащих переменную величину | + |
|
| 5 | При потенцировании логарифмического уравнения (освобождение в процессе решения от знаков логарифмов) | + |
|
| 6 | Преобразования на основе определения логарифма, если в основании переменная | + |
|
| 7 | Деление обеих частей уравнения на одно и то же выражение с переменной (кроме тех случаев, когда точно известно, что всюду в области определения уравнения это выражение не равно нулю) |
| + |
Вариант 1:
Некоторые причины появления посторонних корней при решении логарифмического уравнения:
Вариант 2:
Некоторые причины потери корней при решении логарифмического уравнения:
Существуют и другие «специфические» причины, которые приводят как к появлению, так и к потере корней уравнения, о некоторых из них мы говорили. Но есть и такие, которые, как правило, связаны с определенным классом уравнений, а об этом разговор у нас будет позже.
Исходя из полученных данных укажем несколько рекомендаций:
Как избежать потери корней при решении логарифмических уравнений?
Следить за тем, чтобы в возникающей цепочке уравнений последующее было либо равносильно предыдущему, либо являлось его следствием.
При применении формул, решая уравнение, следить за тем, чтобы область допустимых значений для правой левой частей формулы были одинаковы.
Пользоваться равенствами:
При
…
При …
При
…
При .
При
При
Применяя при решении логарифмических уравнений формулы перехода к новому основанию целесообразной переходить к новому основанию….
(Применяя при решении логарифмических уравнений формулы перехода к новому основанию целесообразной переходить к новому основанию, равному некоторому числу, а не являющемуся выражением с переменной)
Закрепление изученного в процессе решения задач ЕГЭ
Решите логарифмические уравнения из ЕГЭ.
При решении логарифмических уравнений следите за изменением ОДЗ.
(рассмотрите два способа решения)
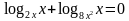
Задание: Найдите ошибку в предложенном решении логарифмического уравнения
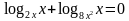
Решение:
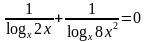
Ответ:
А теперь выполним задание (задания выполняют в парах) (2,3)
Подведение итогов урока, рефлексия
Какова тема урока?
«Преобразования, влияющие на изменение корней логарифмического уравнения»
Какова цель урока?
Цель: Узнать какие преобразования могут изменить корни логарифмического уравнения
Какие задачи с вами решили на уроке?
Задачи:
Выяснили:
- какие преобразования могут привести к потере корней и к появлению посторонних корней при решении логарифмического уравнения;
- как можно избежать потери корней при решении логарифмического уравнения
Можно ли при решении логарифмических уравнений выполнять преобразования, приводящие к расширению ОДЗ?
Как можно избавиться от посторонних корней?
(Сделать проверку).
Можно ли при решении логарифмических уравнений выполнять преобразования, приводящие к сужению ОДЗ?
Как же избежать потери корней?
(При решении уравнения не выполнять преобразования, которые ведут к потере корней).
Домашнее задание
Записать в тетради преобразования, приводящие к потере корней или к приобретению посторонних корней при решении логарифмического уравнения.
Решить уравнения: № 3 (постараться найти несколько способов решения уравнения),
№7, 16 (из предыдущей домашней работы).

 Получите свидетельство
Получите свидетельство Вход
Вход



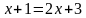
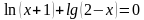
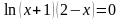
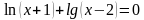
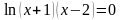
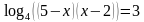
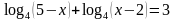
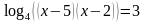
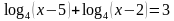
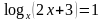
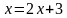
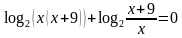
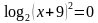
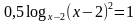
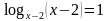
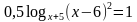
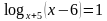
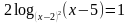
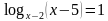
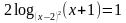
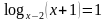









 Конспект урока "Преобразования, влияющие на изменение корней логарифмического уравнения" (37.92 KB)
Конспект урока "Преобразования, влияющие на изменение корней логарифмического уравнения" (37.92 KB)
 0
0 219
219 2
2 Нравится
0
Нравится
0


