Конспект урока «Построение сечений тетраэдра»

Урок по теме «Тетраэдр. Построение сечений». (слайд1)

10 класс

Цель:

образовательная

• ввести понятие тетраэдра;

• проиллюстрировать изученные понятия, связанные со взаимным расположением прямых и плоскостей на примере тетраэдра;

• организовать работу учащихся по выработке умения строить сечения тетраэдра

развивающая

• развивать пространственное мышление,

• создать условия для развития познавательного интереса к предмету.

воспитательная

• воспитывать интерес к математике,

• самостоятельность;

• воспитывать культуру умственного труда.

Оборудование:

• ПК;

• Мультимедийное оборудование;

• Классная доска;

• Учебники;

• Тетради;

• Школьные принадлежности;

• Модели тетраэдра.

1. Оргмомент.

Приветствие, проверка готовности к уроку.

1. Постановка целей и задач урока.

(слайд2)

«Скажи мне – и я забуду.
Покажи мне – и я запомню.
Вовлеки меня – и я научусь.»

Древняя китайская пословица

Перед изучением нового материала учащимся предлагается вспомнить изученный материал о параллельных плоскостях, параллельности прямой и плоскости.

1. Активизация познавательной деятельности. Подготовка к восприятию нового материала.

Учащимся предлагается ответить на вопросы:

(слайды с ответами, комментариями)

1. (слайд 3)Верно ли, что если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны 2-м прямым другой плоскости, то эти плоскости параллельны? (Да. Признак параллельности двух плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны).

2. (слайд 4)

1. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?

(Нет. Если две прямые не имеют общих точек, то они могут быть скрещивающимися)

3.(слайд 5-6)Хорда окружности принадлежит плоскости. Верно ли утверждение, что и вся окружность лежит в этой плоскости?

(Нет, хорда АВ принадлежит плоскости, окружность не принадлежит данной плоскости)

1. (слайд 7)

2. Две прямые параллельны одной плоскости. Можно ли утверждать, что эти прямые параллельны? (Нет. Это могут быть скрещивающиеся прямые)

5. (слайд 8)Прямая пересекает плоскость. Можно ли в плоскости провести прямую, параллельную данной прямой? (Нет, Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.)

1. (слайд 9) Что такое многоугольник? (1)фигура, составленная из отрезков; 2)часть плоскости, ограниченная линией.)

1. Изучение нового материала.

Одна из глав нашего курса будет посвящена многогранникам – поверхностям геометрических тел, составленным из многоугольников.

Но ещё до подробного изучения многогранников сегодня мы познакомимся с одним из них – тетраэдром. Это даст нам возможность проиллюстрировать понятия, связанные со взаимным расположением прямых и плоскостей на примере этих двух геометрических тел.

Сегодня мы рассмотрим один из них, это тетраэдр.

(слайд 10) Рассмотрим произвольный треугольник АВС и точку Д, не лежащую в плоскости этого треугольника. Соединив точку Д отрезками с вершинами треугольника АВС, получим фигуру, которую назовём тетраэдром.

(слайд 11) Название этого многогранника пришло из Древней Греции, и в нём указывается число граней:

«тетра» - 4

«эдра» - грань

(слайд 12)Тетраэдр является одним из правильных многогранников, которые мы рассмотрим на дальнейших наших уроках.

(слайд 13) Правильные многогранники иногда называют платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном жившим около 348 г до нашей эры.

Платоновыми телами являются:

(слайд 14) Гексаэдр, Тетраэдр, Октаэдр, Икосаэдр, Додекаэдр.

(слайд 15) Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников, где Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у пламени.

(слайд 16) В жизни мы встречаемся с тетраэдром например в химии

Молекула метана СН4 имеет форму правильного тетраэдра. Этот факт подтверждается фотографиями молекулы метана, полученными при помощи электронного микроскопа.

Чтобы дать определение тетраэдра введём некоторые геометрические понятия.

(слайд 17)

Плоскость тела – грань

Прямая пересечения плоскостей – ребро

Точка пересечения прямых – вершина

У меня на столе имеются различные геометрические тела и сейчас представитель каждой парты выберет среди них тетраэдр, будьте внимательны.

Выбрали все верно хотя у меня на столе была фигура очень похожая на тетраэдр, но имеет она в основании другой многоугольник, это пирамида.

(слайд 18) Сейчас в тетради запишите число, тему «Тетраэдр. Сечение тетраэдра», и сделаем практическую работу.

Рассмотрите пожалуйста геометрическое тело внимательно и запишите в тетрадях следующие данные:

(Слайды19-22) Сколько у тетраэдра вершин, граней, и рёбер?

Какими геометрическими фигурами являются грани?

Давайте самостоятельно дадим определение тетраэдра.

(слайд 23) обобщим определение тетраэдра.

Тетраэдр – поверхность, составленная из четырех треугольников (DABC). Треугольники, из которых состоит тетраэдр называются гранями ADB, ADC, BCD, ABC, их стороны – ребрами AD, BD, DC, AC, AB, BC, вершины – вершинами тетраэдра D, A, B, C.

Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.

Одну грань ABC называют основанием, а три другие – боковыми гранями.

Два ребра тетраэдра, не имеющие общих вершин, называются противоположенными( назвать самостоятельно по рисунку )

Как же на плоскости изобразить объемную фигуру, такую как тетраэдр?

(слайд 24 )

1. Строим основание в виде разностороннего треугольники

2. Ставим точку вне плоскости основания.

Соединяем вершины треугольника отрезками с этой точкой.

Видимые линии - сплошные

Не видимые – пунктиром

Обозначение тетраэдра начинают с вершины: DABC; SABC.

Сейчас в тетрадях начертите любой тетраэдр и обозначьте его: МКРА

Какой треугольник является основанием? Какая точка – вершина?

А сейчас рассмотрим задачи связанные с тетраэдром.

Мы рассмотрим с вами построение сечения в тетраэдре

Что же такое сечение?

Сечение-это изображение предмета мысленно пересеченное плоскостью или несколькими плоскостями.

Что же такое сечение тетраэдра?

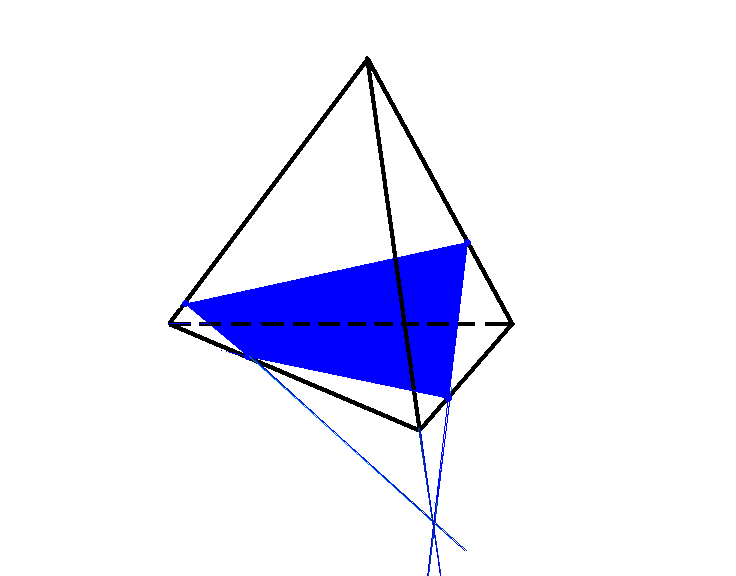
• Многоугольник, сторонами которого являются отрезки по которым секущая плоскость пересекает грани тетраэдра называется сечением тетраэдра

(слайд 25) Какими многоугольниками могут быть сечения?

Так как тетраэдр имеет четыре грани, то его сечениями могут быть треугольники, четырёхугольники

Чтобы начать строить сечения мы должны с вами вспомнить некоторые геометрические утверждения

(слайд 26)

ПАМЯТКА

• Соединять можно только две точки, лежащие в плоскости одной грани.

• Секущая плоскость пересекает параллельные грани по параллельным отрезкам.

• Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.

(слайды 27-33) Практическая работа: Построение сечения.

№1 Построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K

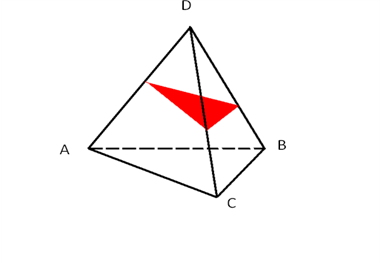
№2. Построить сечение тетраэдра плоскостью, проходящей через точки E, F, K.

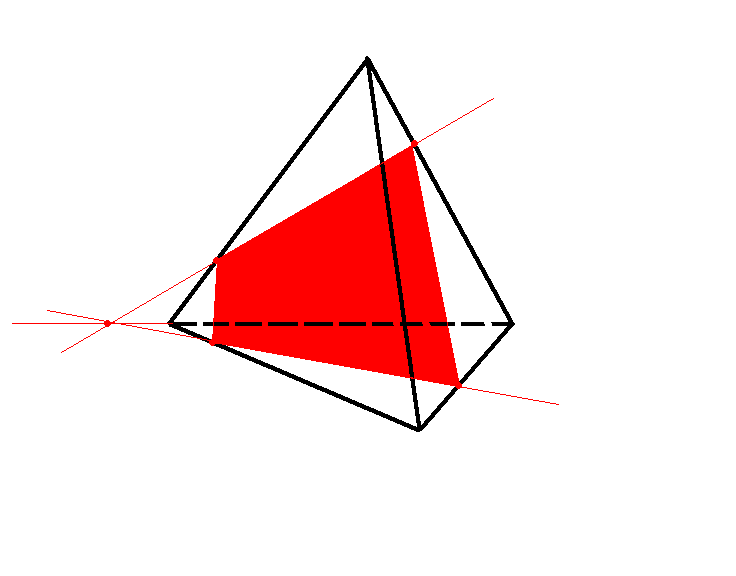
№3. На ребрах AC, AD, DB тетраэдра – DABC. Отмечены точки M,N,P. Построить сечение тетраэдра плоскостью MNP.

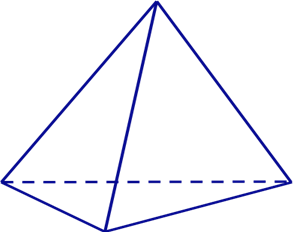
№4. Построить сечение тетраэдра плоскостью, проходящей через точки E, F, K.

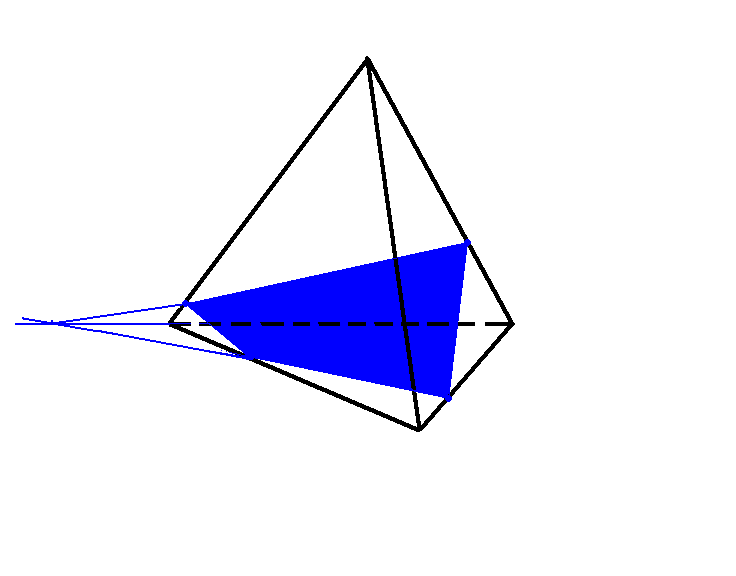
(Слайд 34) ИТОГ УРОКА:

1. О каком многограннике шла речь сегодня на уроке?

2. Какие задачи мы научились сегодня решать?

3. Какие действия должен уметь выполнять ученик для построения сечений многогранников? (находить точки пересечения прямой и плоскости; строить линию пересечения двух плоскостей)

ДОМАШНЕЕ ЗАДАНИЕ:

Стр 24-29

П.12, 14

1) Выполнить задания по построению сечения тетраэдра (по карточкам).

2) Творческое задание (по желанию): изготовить бумажную модель тетраэдра.

Самоанализ урока.

Урок «Тетраэдр. Построение сечений» завершает изучение темы «Параллельность прямой и плоскости», которая является первой при изучении темы стереометрии – раздела геометрии. Одной из основных задач геометрии является формирование пространственного представления, и данный урок позволяет выполнить эту задачу.

На уроке спланировано включение учащихся в осознанную деятельность.

Избранные методы: информационные (объяснение с демонстрацией наглядных пособий) и репродуктивные (беседа с элементами самостоятельной работы) и формы организации познавательной деятельности были нацелены на достижение триединой цели урока.

Задачей на уроке было организовать деятельность учащихся таким образом, чтобы подвести их к теме урока, познакомить их с понятиями тетраэдра, а так же научить строить сечения.

На первом этапе урока, используя проблемный вопрос, определили темы урока и цела.

На этапе (изучение нового материала) показать возможные сечения тетраэдра, научиться строить разные сечения.

Этап закрепления предполагал возможность учащихся самостоятельно построить различные сечения параллелепипеда.

ИТОГ урока.

В конце урока проведена рефлексия, которая побуждала учащихся к самоанализу и оценке деятельности.

Домашнее задание позволит учащимся поработать с учебником.