Конспект урока по теме "Признак параллельности прямой и плоскости"

Тема урока: «Признак параллельности прямой и плоскости».

Тип урока: ознакомление с новым материалом.

Цели урока:

Образовательная: рассмотреть взаимное расположение прямой и плоскости в пространстве; доказать признак параллельности прямой и плоскости; свойства параллельности прямой и плоскости.

Развивающая: развивать конструктивные способности и навыки решения задач.

Воспитывающая: воспитывать ответственное отношение к учебе.

Средства обучения:

Технические: мультимедийная система, интерактивная доска.

Художественно-изобразительные (цифровые материалы): электронная презентация к повторению, объяснению нового материала и к задачам при закреплении.

Оборудование: линейки, карандаши, прибор по стереометрии.

План урока:

I. Повторение изученного материала:

1. С помощью схемы: «Взаимное расположение двух прямых в пространстве» вспомним определение параллельных прямых.

Слайд №2:

Ответ: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.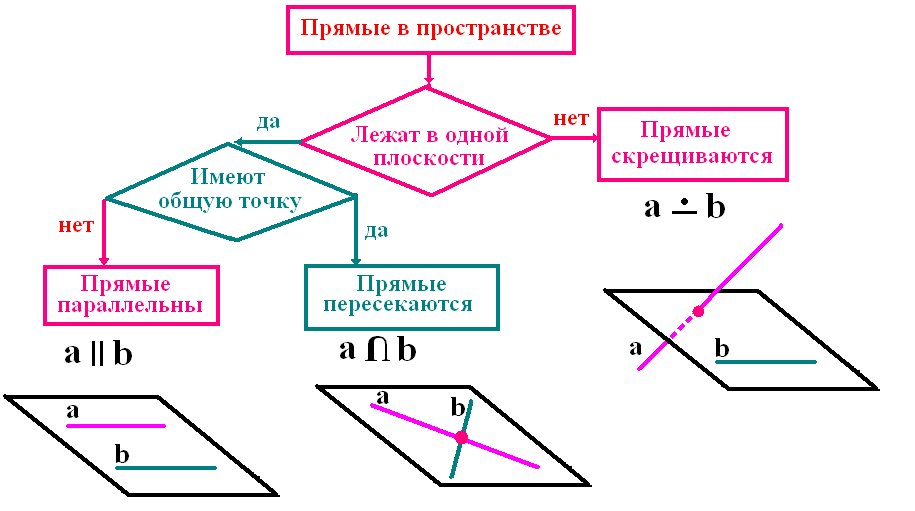

2. Всегда ли через две параллельные прямые можно провести плоскость? Почему?

Ответ: Всегда, потому, что две параллельные прямые лежат в одной плоскости.

3. Какие прямые называются пересекающимися?

Ответ: Две прямые в пространстве называются пересекающимися, если они имеют одну общую точку.

4. Дайте определение скрещивающихся прямых.

Ответ: Прямые, которые не пересекаются и не лежат в одной плоскости называются скрещивающимися.

5. Определить взаимное расположение прямых АВ и СД (ответ пояснить)

Слайд №3:

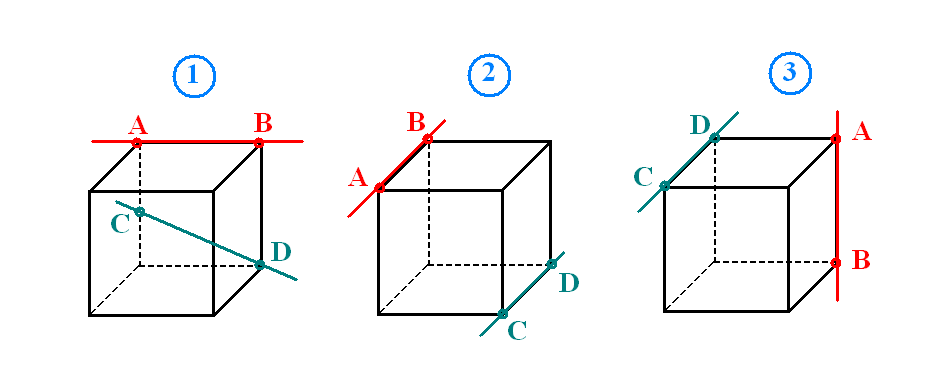
II. Работа по теме:

1. Посмотрим на разнообразие прямых существующих вокруг нас.

Слайд №4: «Прямые вокруг нас».

2. Разберемся с расположением прямой и плоскости в пространстве. Рассмотрим схему:

Слайд №5:

а) Прямая лежит в плоскости…

Если две точки прямой принадлежат плоскости, то вся прямая лежит в этой плоскости.

б) Прямая пересекает плоскость…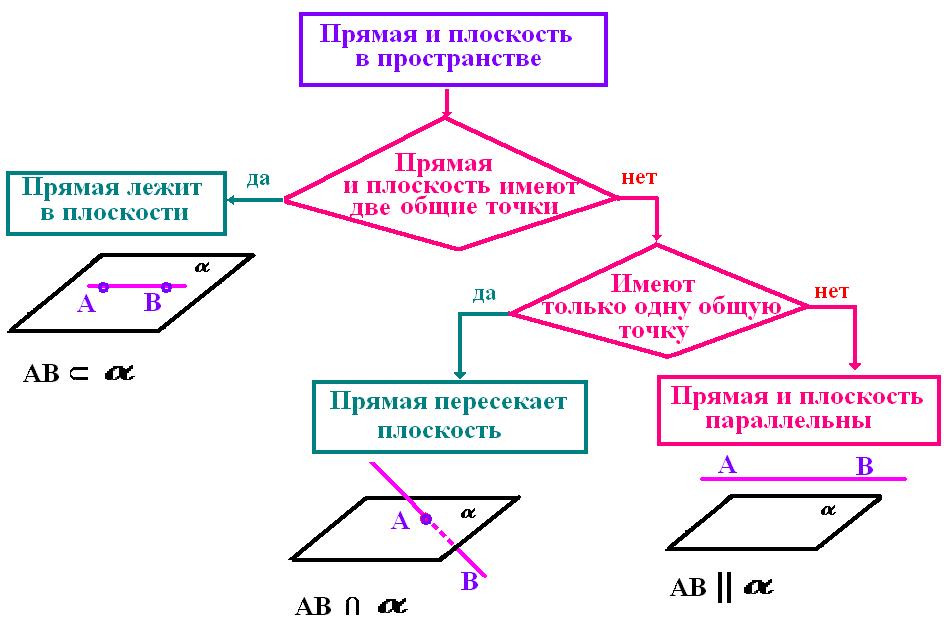

Прямая пересекает плоскость, если имеет одну общую точку.

в) Прямая и плоскость параллельны…

Прямая и плоскость параллельны, если они не пересекаются.

Выполнить чертеж в) и сделать запись.

3. Теорема 17.3 (стр.13)

Слайды №6,7: «Признак параллельности прямой и плоскости».

Если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то данная прямая параллельна плоскости.

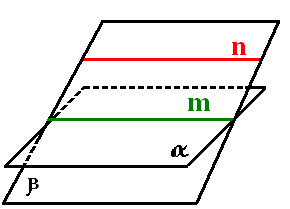
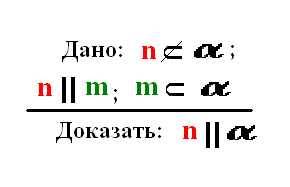
Доказательство:

1) Через прямые n и m проведем плоскость β. (плоскость α и β – различные) Достраиваем плоскость β.

2) Плоскость α пересекается с плоскостью β по прямой m. Что это значит? – Это значит, что все общие точки плоскостей α и β лежат на прямой m.

3) Если бы прямая n пересекала плоскость α, то их общая точка принадлежала бы прямой m, что невозможно, так как n ׀׀ m, следовательно, n ׀׀ α. ч. т. д.

4. Слайд №8: «Свойства параллельности прямой и плоскости».

1) Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Доказательство:

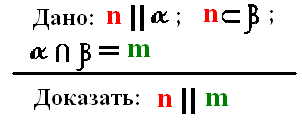
Действительно, прямые n и m лежат в плоскости β и не пересекаются: ведь в противном случае прямая n пересекала бы плоскость α, что невозможно, поскольку n ׀׀ α. ч. т. д.

2) Если одна из двух параллельных прямых, не лежащих в данной плоскости, параллельна этой плоскости, то другая прямая тоже параллельна этой плоскости.

Доказательство: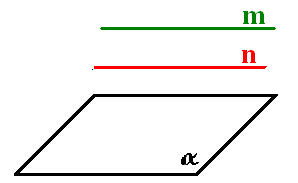

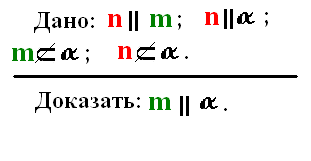
n ׀׀ α – по условию, следовательно n не пересекает плоскость α, по определению. (прямая и плоскость параллельны, если они не пересекаются)

m – не пересекает плоскость α, так как n ׀׀ m. ч. т. д.

III. Закрепление:

Задание 1.

Слайд №9: Определить взаимное расположение прямой АВ и плоскости α.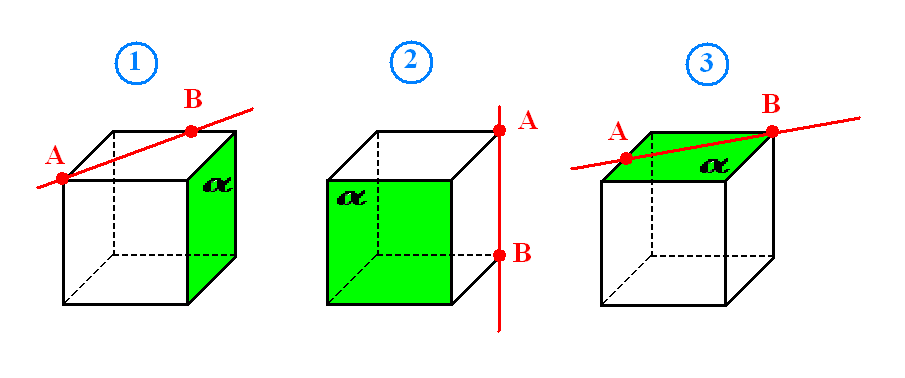

Задание 2.

Слайд №10: Определить взаимное расположение прямых АВ, СД, КМ и плоскости α.

АВ ∩ α, СД ׀׀ α.

Задача №16 стр.20.

Слайд №11,12: Докажите, что через любую из двух скрещивающихся прямых можно провести плоскость, параллельную другой прямой.

Дано: а, в – прямые,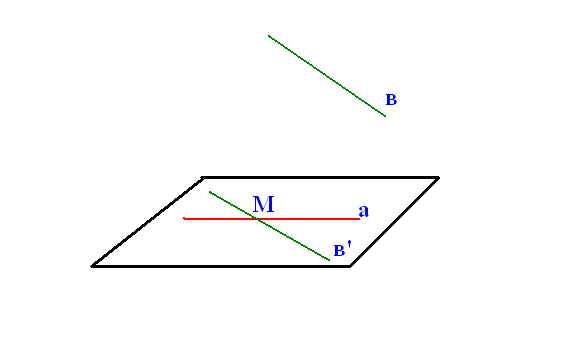

а в; а α.

Доказать: в׀׀ α.

Доказательство:

1. По аксиоме плоскости С₁ на прямой а выберем точку М а.

2. Через точку М проведем в ׀׀ в, так как через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну.

3. По аксиоме существования плоскостей С₃ построим плоскость α.

4. Так как в ׀׀ в и в лежит в плоскости α, то в ׀׀ α по признаку параллельности прямой и плоскости. ч. т. д.

Аналогично, можно доказать и для другой прямой.

IV. Итог урока:

1. Что узнали нового? – рассмотрели взаимное расположение прямой и плоскости; изучили теорему о признаке параллельности прямой и плоскости; свойства параллельности прямой и плоскости.

2. Сформулируйте признак параллельности прямой и плоскости.

3. Что значит: прямая и плоскость параллельны? - прямая и плоскость параллельны, если они не пересекаются.

4. Одна из двух параллельных прямых параллельна некоторой плоскости. Верно ли утверждение, что и вторая прямая параллельна этой плоскости? – да, по 2 свойству параллельности прямой и плоскости.

V. Домашнее задание:

Слайд №13: Вопросы 5,6 стр.18, пункт 143.

Задача №15 стр.13: Докажите, что если плоскость пересекает одну из двух параллельных прямых, то она пересекает и другую.