Конспект урока по теме
«Построение сечений в многогранниках методом следов»
| | ФИО: Грязнова Татьяна Геннадьевна |
| | Место работы: МБОУ «Черновская средняя школа» Большеболдинского района Нижегородвкой области |
| | Должность: учитель математики |
| | Предмет: геометрия |
| | Класс: 10 |
| | Тема урока: «Построение сечений в многогранниках методом следов» |
| | Базовый учебник: Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 10 – 11: – М.: Просвещение, 2010. |
Цели урока:
Формирование у учащихся навыков решения задач на построение сечений методом следов.
Формирование и развитие у учащихся пространственного воображения.
Развитие графической культуры и математической речи.
Воспитание чувства сплоченности, взаимопомощи, умения работать индивидуально над задачей.
Оборудование: компьютер, мультимедийный проектор, интерактивная доска, программа «Живая математика», презентация, ноутбуки для учащихся.
План урока.
Организационный момент.
Постановка учебной задачи.
Изучение нового материала.
Решение задач на построение сечений.
Подведение итогов урока, домашнее задание.
Ход урока
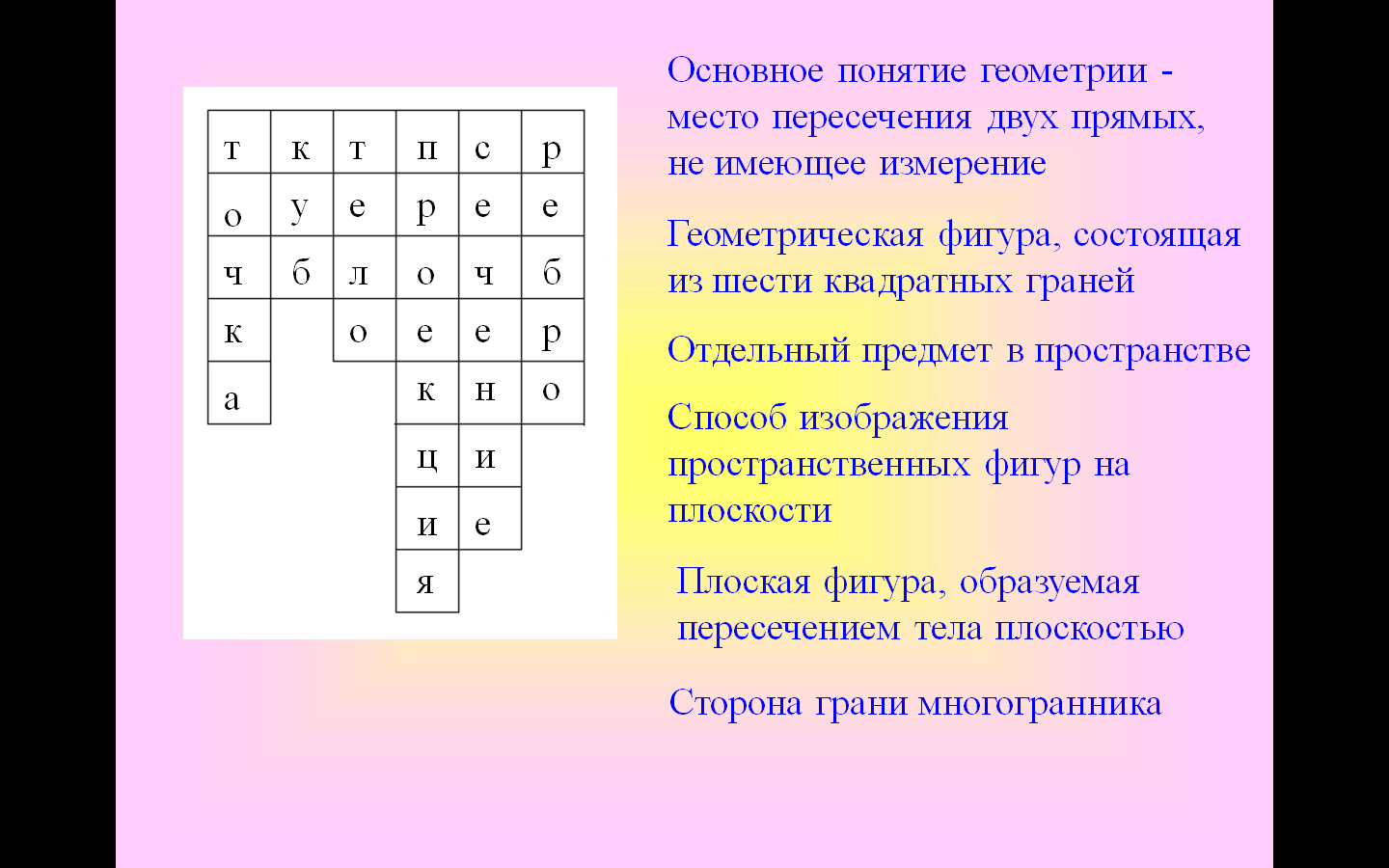
Ребята, я предлагаю вам повторить и вспомнить некоторые геометрические понятия и определения (слайд 1 – кроссворд).
 .
.
Основное понятие геометрии – место пересечения двух прямых, не имеющее измерения
Геометрическая фигура, состоящая из шести квадратных граней.
Отдельный предмет в пространстве.
Способ изображения пространственных фигур на плоскость.
Плоская фигура, образуемая пересечением тела плоскостью.
Сторона грани многогранника.
Ответы:
1. Точка 2. Куб 3. Тело 4. Проекция 5. Сечение 6. Ребро
Тема нашего урока: « Построение сечений в многогранниках методом следов».
Вы изучили аксиомы стереометрии, следствия из аксиом, теоремы о параллельности прямых и плоскостей в пространстве. При решении многих стереометрических задач используют сечение многогранника плоскостью. Существует несколько методов построения сечений многогранника плоскостью: метод следов, метод внутреннего проектирования и комбинированный метод. Мы изучим метод следов.
В черчении есть определение: Сечение – это изображение фигуры, которая получается при мысленном рассечении тела плоскостью. Вот таким определением мы и будем пользоваться сегодня на уроке. (слайды 3)
Слайд4

Слайд5 
Слайд6 
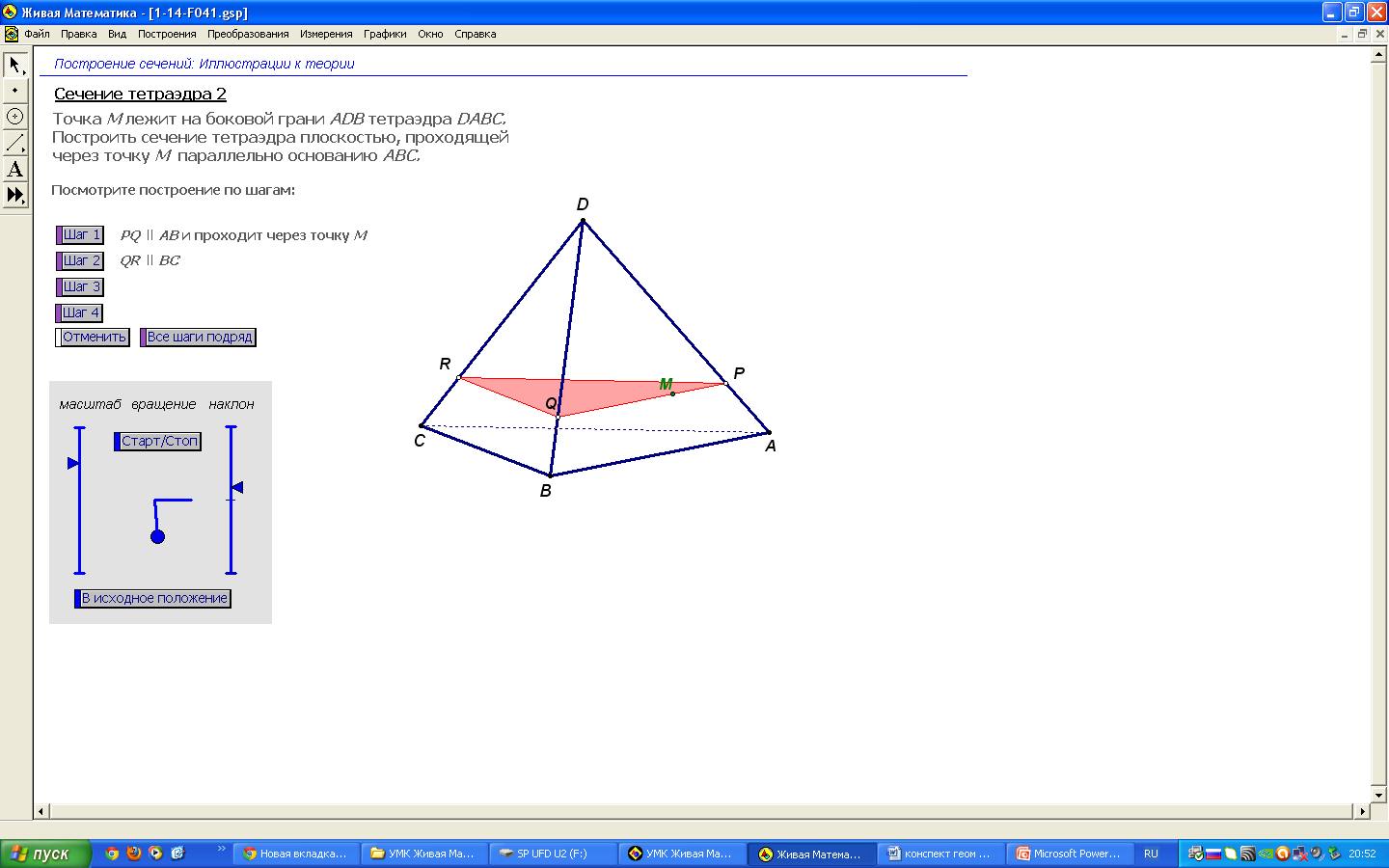
Рассмотрим пример построения сечения тетраэдра плоскостью параллельной основанию.
Программа «Живая математика»
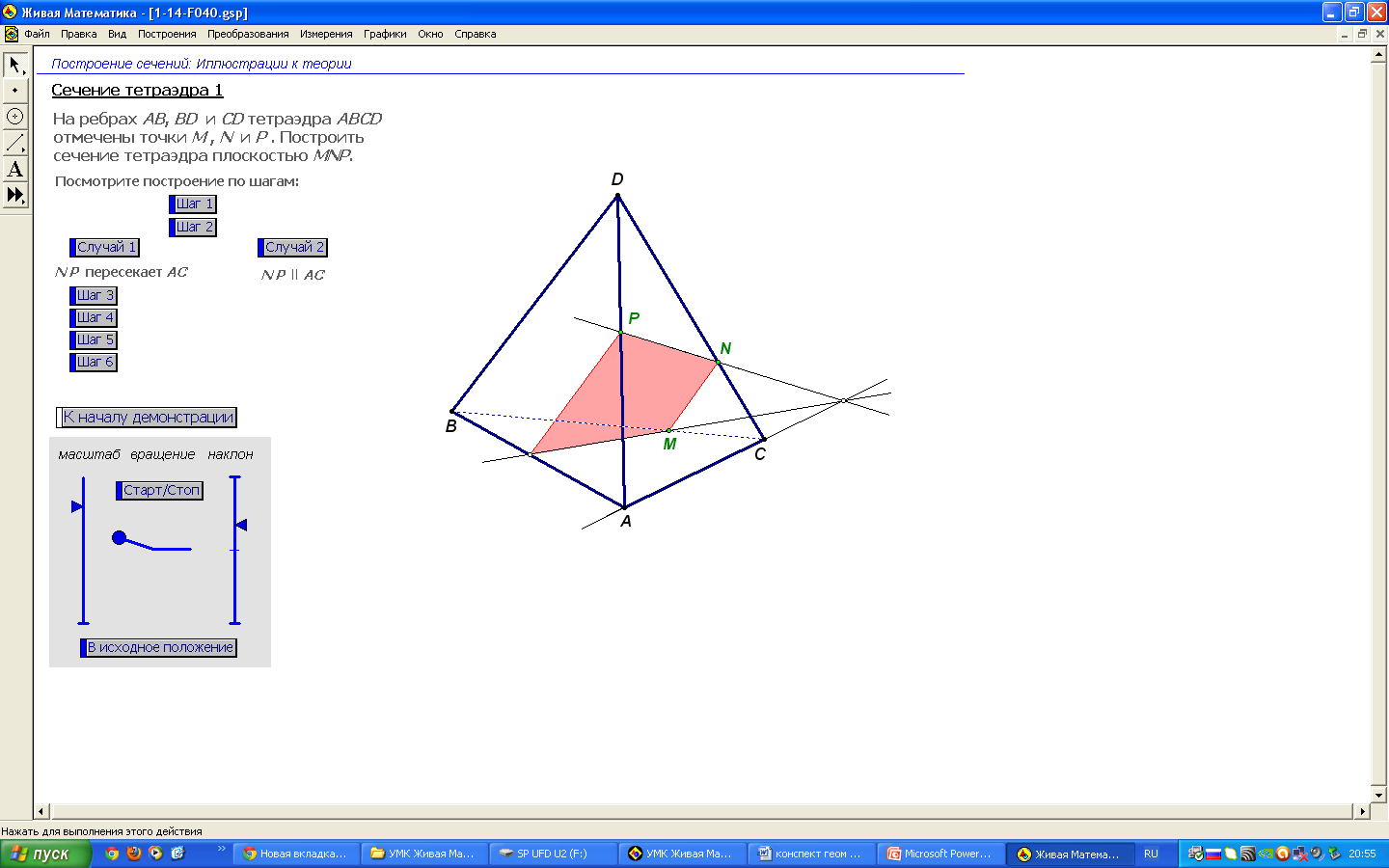
Рассмотрим метод следов при построении сечения тетраэдра плоскостью, проходящей через 3 точки.
Решить задачу № 79 (а) из учебника. Ученики выполняет построение в программе «Живая математика».
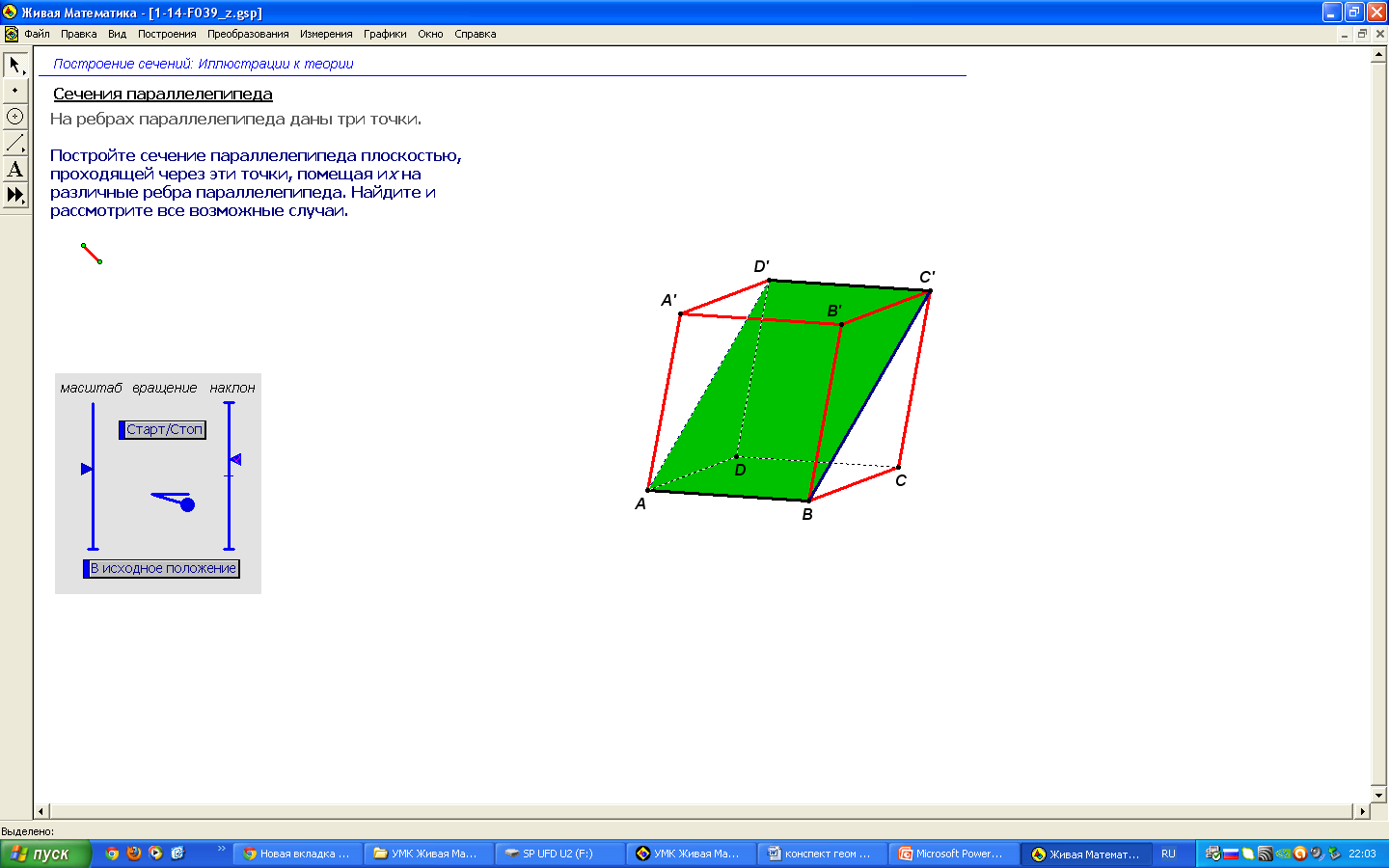
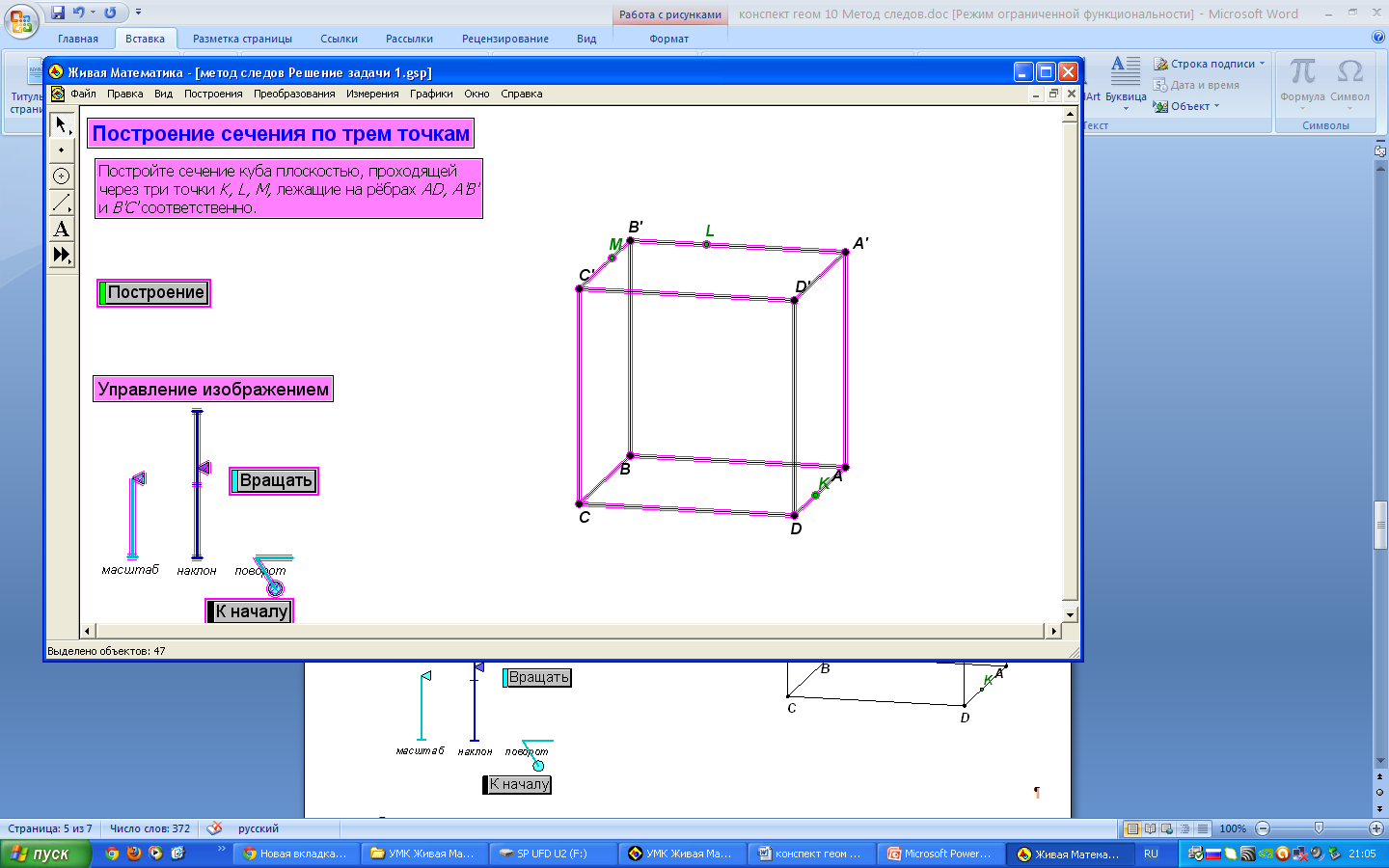
Постройте сечение куба плоскостью, проходящей через три точки K, L, M, лежащие на рёбрах AD, A'B' и B'C' соответственно. (программа - живая математика задача 1 построение сечений куба).
|
|
|
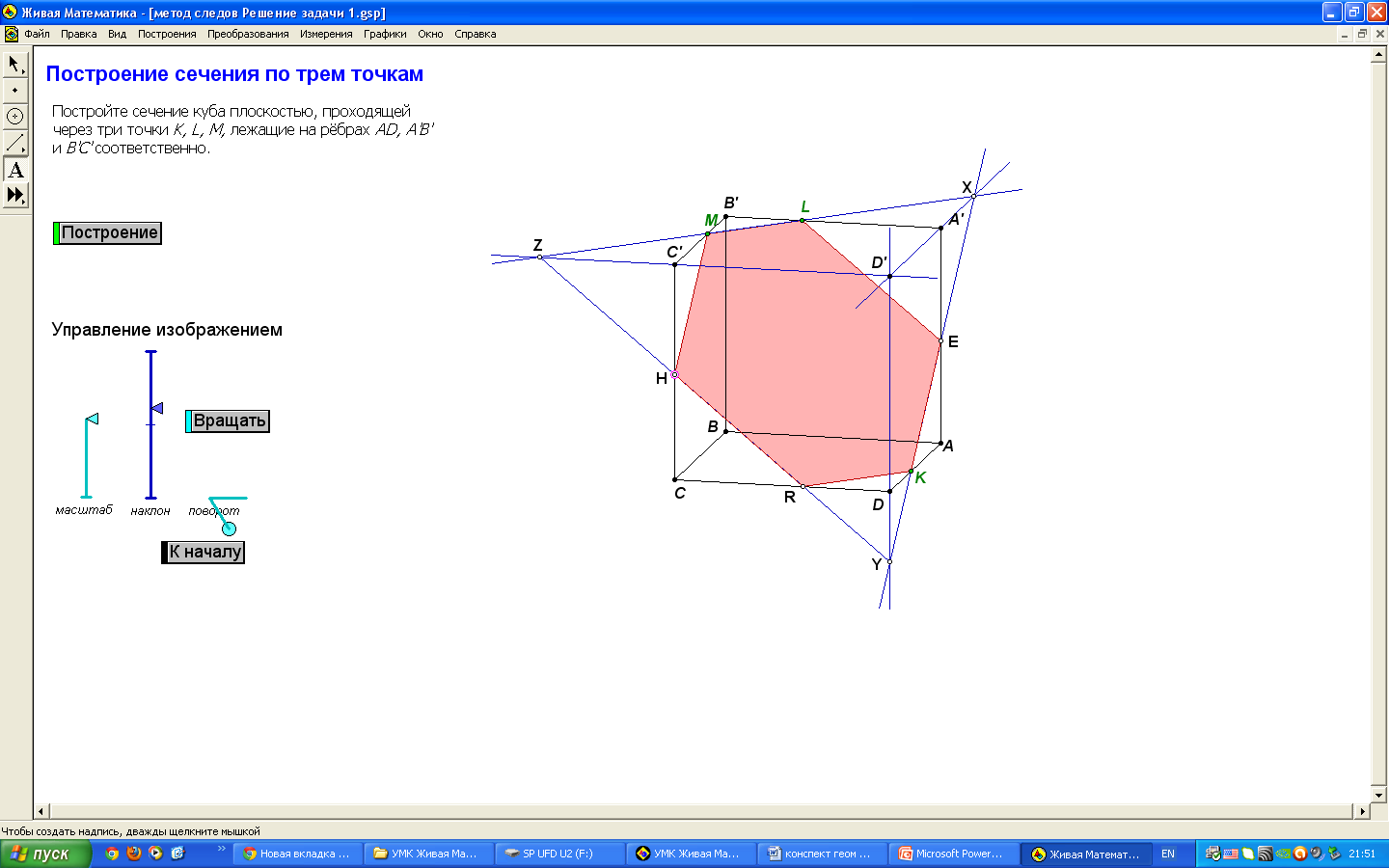
Алгоритм построения (слайд 7)
Соединить точки M и L.
Построить пересечение прямых ML и D'A'. Обозначим точку Х.
Находим линию пересечения плоскости β с гранью AA'D'D, проводим прямую XK.
Построить пересечение прямых XK и D'D. Обозначим точку Y.
Построить пересечение прямых ML и D'C'. Обозначим точку Z.
Соединить точки Z и Y.
Соединив последовательно точки, получим искомое сечение β.
Подведение итога урока.
Что называется сечением?
Что может получится в результате сечения тетраэдра и параллелепипеда?
Как построить сечение методом следов?
Домашнее задание:
п.14, № 80, № 75.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект урока по теме «Построение сечений в многогранниках методом следов» с применением алгоритма построения. (997 KB)
Конспект урока по теме «Построение сечений в многогранниках методом следов» с применением алгоритма построения. (997 KB)
 0
0 184
184 5
5 Нравится
0
Нравится
0


