Муниципальное бюджетное общеобразовательное учреждение «Подвязновская средняя школа» Ивановского района Ивановской области
Конспект урока в 8 классе
учителя высшей квалификационной категории Ражевой Н.В.
Тема урока: Площадь трапеции.
Тип урока: урок изучения и первичного закрепления новых знаний.
Цель: изучение и первичное восприятие формулы площади трапеции, осмысление
связей и отношений к объекту изучения.
Задачи:
Вывести формулу площади трапеции методом разбиения, рассмотреть различные подходы.
научиться заполнять таблицу по опорным знаниям (таблица – опорный сигнал для дальнейшего вывода формулы).
показать разнообразие подходов к решению одной задачи.
применять знания в практической деятельности.
| № п.п. | Этапы урока | Содержание этапа. Деятельность педагога. | Деятельность учащихся. | ||||||||||||||||||
| 1 | Организация и начало урока | Приветствие учащихся: Здравствуйте, ребята. Сегодня у нас урок получения новых знаний. Эпиграф урока: «Знание – самое превосходное из владений, все стремятся к нему. Само оно не приходит!»- (1 слайд) и, поэтому, предлагаю вам поработать на уроке под девизом: «Все в ваших руках». |
| ||||||||||||||||||
| 2 | Мотивация учебной деятельности | Разгадайте ребус: (2 слайд)
Как вы поняли, сегодня на уроке предметом нашего внимания будет трапеция Дайте определение трапеции.
У трапеции, как у любого многоугольника, можно найти… (метод недописанного тезиса). Как найти периметр трапеции? Площадь? Сегодня на уроке мы с вами выведем формулу для нахождения площади трапеции. |
Трапеция
-это четырехугольник, две стороны которого параллельны, а другие две нет.
периметр, площадь.
-формулы не знаем. | ||||||||||||||||||
| 3 | Актуализация опорных знаний | Площади каких фигур вы уже научились находить? Заполните, пожалуйста, таблицу формул.
Рекомендации: стороны фигур обозначить малыми буквами a, b, с высоту: h
Какие фигуры в геометрии называются равными?
Что можно сказать о площадях равных фигур? В основу измерения площадей положено утверждение: Площадь фигуры, составленной из непересекающихся фигур, равна… (энциклопедический словарь юного математика) И поэтому, при вычислении площадей многоугольников используется простой прием, называемый методом разбиения. | Квадрата, прямоугольника, параллелограмма, треугольника
Самопроверка: верно: + неверно: -
«5» - все верно, «4» – верно 4 «3» – верно 3, «2» - верно 2 и меньше.
- которые совмещаются наложением.
-они равны.
-сумме их площадей
| ||||||||||||||||||
| 4 | Изучение нового материала | Каким способом можно разбить трапецию на фигуры, площади которых мы умеем находить?
Работа в группах – 4 Опорный сигнал: Обозначьте необходимые элементы фигур малыми буквами достройте недостающие для определения площади. Запишите площадь каждой фигуры. Найдите площадь трапеции, как сумму площадей фигур, из которых она состоит. Упростите получившуюся формулу. Оказание педагогической поддержки в случае необходимости.
Какая формула для нахождения площади трапеции у вас получилась?
«Да, путь познания не гладок, но знаем мы со школьных лет, загадок больше чем разгадок, и поискам предела нет». (Татьяничева)
В энциклопедическом словаре юного математика сказано: «Площадь составной фигуры не изменится, если ее части расположить по-другому, но опять без пересечения. Две фигуры, имеющие разную форму, но одинаковые площади называются равновеликими. Предлагается вниманию учащихся доказательство площади трапеции с использованием интернет сайта http//www.etudes.ru/ru/etudes/. Математические этюды. | Перебор способов: 1
2
3
4
S =
Отчет каждой группы о проделанной работе.
| ||||||||||||||||||
| 5 | Первичная проверка усвоения знаний | Найдите площадь трапеции, изображенной на рисунке: 15 8 13
9 12 Какие элементы трапеции надо знать, чтобы найти ее площадь? (основания и высоту)
|
a= 7 b =9 + 12 =21 h = 8 S = = 14 | ||||||||||||||||||
| 6 | Подведение итогов урока. Рефлексия | Что нового вы узнали на сегодняшнем уроке?
Возьмите, пожалуйста, в руки фигуру, которая соответствует одному из содержаний, которое вы испытали на уроке сегодня. И на этой фигуре поставьте +, если урок понравился, - если урок не понравился. | С. 127. Чтение теоремы о площади трапеции.
Я понял, как находить площадь трапеции.
Я узнал много подходов к доказательству теоремы.
Я испытывал затруднения при выводе новой формулы. | ||||||||||||||||||
| 7 | Информация о домашнем задании | п.53, № 480 |
|
Литература:
Учебник «Геометрия7-9», Л.С.Атанасян, В.Ф.Бутузов и др.
Энциклопедический словарь юного математика.
Использование: интернет ресурсов и ИКТ.
Опорный сигнал:
Обозначьте необходимые элементы фигур малыми буквами
достройте недостающие для определения площади.
Запишите площадь каждой фигуры.
Найдите площадь трапеции, как сумму площадей фигур, из которых она состоит.
Упростите получившуюся формулу.
________________________________________________________________________
Опорный сигнал:
Обозначьте необходимые элементы фигур малыми буквами
достройте недостающие для определения площади.
Запишите площадь каждой фигуры.
Найдите площадь трапеции, как сумму площадей фигур, из которых она состоит.
Упростите получившуюся формулу.
________________________________________________________________________
Опорный сигнал:
Обозначьте необходимые элементы фигур малыми буквами
достройте недостающие для определения площади.
Запишите площадь каждой фигуры.
Найдите площадь трапеции, как сумму площадей фигур, из которых она состоит.
Упростите получившуюся формулу.
________________________________________________________________________
Опорный сигнал:
Обозначьте необходимые элементы фигур малыми буквами
достройте недостающие для определения площади.
Запишите площадь каждой фигуры.
Найдите площадь трапеции, как сумму площадей фигур, из которых она состоит.
Упростите получившуюся формулу.

 Получите свидетельство
Получите свидетельство Вход
Вход








 .
.
 .
. 


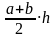



 7
7








 Конспект урока по геометрии "Площадь трапеции" (94.33 KB)
Конспект урока по геометрии "Площадь трапеции" (94.33 KB)
 0
0 677
677 20
20 Нравится
0
Нравится
0









