Конспект урока для дистанционного обучения учащихся

Карта урока для организации занятий с использованием

дистанционных технологий обучения

Учитель: Побегуца Светлана Владимировна

Предмет: математика

Класс: 10 А

Дата проведения урока: 6 апреля 2020 года, 7 апреля 2020 года

Если проблемы с виртуальной школой:

Выполненное практическое задание необходимо предоставить в любом доступном формате (скан, фотография, документ MS Word)

- электронным письмом на адрес [email protected]

Название файла (сообщение) должно содержать название предмета, фамилию ученика и класс. Например: физикаИванов9А.doc

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №34. Формулы сложения (сайт РЭШ Раздел Алгебра и начала математического анализа 10 класс Урок 34 Формулы сложения https://resh.edu.ru/subject/lesson/4734/main/199309/)

Перечень вопросов, рассматриваемых в теме:

• формулы синуса суммы и разности аргументов; косинуса суммы и разности аргументов; тангенс суммы и разности аргументов;

• преобразование тригонометрических выражений на основе использования формулы синуса, косинуса, тангенса и котангенса суммы и разности аргументов;

• вычисление значения тригонометрических выражений на основе формулы синуса, косинуса, тангенса и котангенса суммы и разности аргументов;

• доказательство тригонометрических тождеств на основе формулы синуса, косинуса, тангенса и котангенса суммы и разности аргументов.

Глоссарий по теме

Формулы сложения - это формулы синуса суммы и разности аргументов; косинуса суммы и разности аргументов; тангенс суммы и разности аргументов.

.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Рассмотрим единичную окружность в прямоугольной системе координат хОу. (рис. 1)

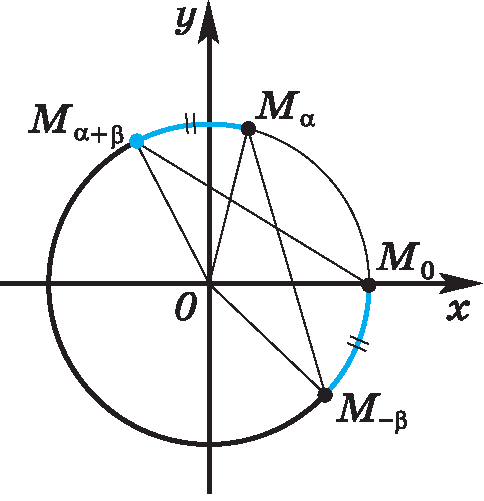
Рисунок 1 – единичная окружность

Точка   получена поворотом точки Мₒ(1;0) на угол   , а точка   на угол   и точка   на угол  .

Углы   и   равны, отрезки  . Значит, треугольник   равен треугольнику   , следовательно у них одинаковые стороны   и  .

Так как синус это ордината точки на единичной окружности, а косинус её абсцисса, то точки имеют координаты

;

;

).

Подставим координаты точек   и   в формулу для нахождения расстояния между ними. Получим:

.

Преобразуем левую часть, используя формулы квадрата суммы и разности двух выражений и тригонометрические тождества:

Преобразуем правую часть:

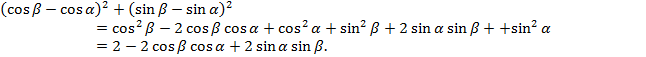
Соединим левую и правую части:

Разделим на  каждое слагаемое :

Получили формулу косинуса суммы.

Заменим   и учтём, что  , получим формулу косинуса разности

Докажем, что 

Так как  ,  , то по формуле косинуса разности получаем:

 Заменим   получим

Так, например, , потому что  .

Докажем, что 

Подставим в формулу   значение  , получим:

Для тангенса и котангенса тоже справедливы формулы

Выведем формулу синуса суммы и разности:

.

В этой формуле заменим   и получим формулу синуса разности:

Для тангенса тоже есть формула суммы и разности. По определению  .

Тогда tg  , разделим числитель и знаменатель на

Получаем формулу тангенса суммы  .

Заменим в ней   и учтём, что tg⁡〖(-α)=〖-tg〗⁡α 〗, получим формулу тангенса разности

.

Пример. Вычислим  .

Для котангенса суммы и разности применяют формулы:

Примеры и разбор решения заданий тренировочного модуля

Пример 1. Найти 

Решение: Представим  , так как нам известны значения косинуса углов   и   Подставим в формулу косинуса суммы. Получаем:

.

Ответ:  .

Пример 2. Найти  .

Решение: Представим  , так как нам известны значения синуса углов   и   Подставим в формулу синуса суммы. Получаем:

.

Ответ:  .

Пример 3. Вычислите  .

Решение: Применяем формулу синуса разности:  .

Ответ:  .

2. Просмотрев Урок 34 на сайте РЭШ, сделать в своих тетрадях записи формул и примеров.

3. Домашнее задание: Выполнить тренировочные задания данного урока, сделать скриншот результата+ решение в тетради.