Конспект урока "Десятичная запись дробных чисел" Тип урока: урок открытия новых знаний.

Конспект урока.

Тема: «Десятичная запись дробных чисел» (5 класс)

Цели урока:

Образовательная: сформировать понятие «десятичная дробь».

Воспитательная: воспитывать аккуратность и настойчивость в достижении цели.

Развивающая: способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления.

Оборудование: учебник, презентация «Десятичная запись дробных чисел»

Тип урока: урок открытия новых знаний.

Ход урока.

1. Подготовительный этап:

Цель: актуализировать знания (единицы измерения длины, позиционная запись цифр в числе, разряд числа, целая и дробная часть числа).

Метод: репродуктивный.

Форма: фронтальный опрос.

Ход:

Учитель: Здравствуйте ребята! Откройте тетради, запишите в них число и «Классная работа».

Давайте вспомним, какие мы знаем единицы измерения длины?

Дети: Миллиметры, сантиметры, дециметры, метры, километры.

Учитель: Правильно, молодцы. А как эти единицы измерения связаны между собой? Сколько миллиметров в 1 сантиметре?

Дети: В сантиметре 10 миллиметров.

Учитель: Какую часть сантиметра составляет 1 мм?

Дети: 1 мм это 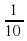часть сантиметра.

Учитель: Сколько сантиметров в 1 метре?

Дети: В 1 метре 100 сантиметров.

Учитель: Какую часть метра составляет 1 см?

Дети: 1 см – это 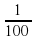часть метра.

Учитель: Выразите 6 дм 3 см в дм. (числовые выражения фиксируются на доске и в тетрадях)

Ученик у доски: .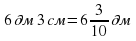

Учитель: Как называется получившееся число.

Дети: У нас получилось смешанное число.

Учитель: Чему равны целая и дробная часть смешанного числа?

Дети: Целая часть равна 6, а дробная часть равна .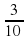

Учитель: Какую часть метра составляют 72 см?

Ученик у доски: 72 с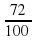м = м.

Учитель: Какую часть км составляет 305 м?

Ученик у доски: 305 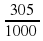м = км.

Учитель: Посмотрите внимательно, что общего у всех полученных дробей?

Дети: У всех дробей в знаменателе находится единица и нули.

Учитель: Да, молодцы. Действительно, в знаменателе этих дробей записана разрядная единица. Чтобы освежить в памяти это понятие, посмотрите не слайд. (Слайд 1)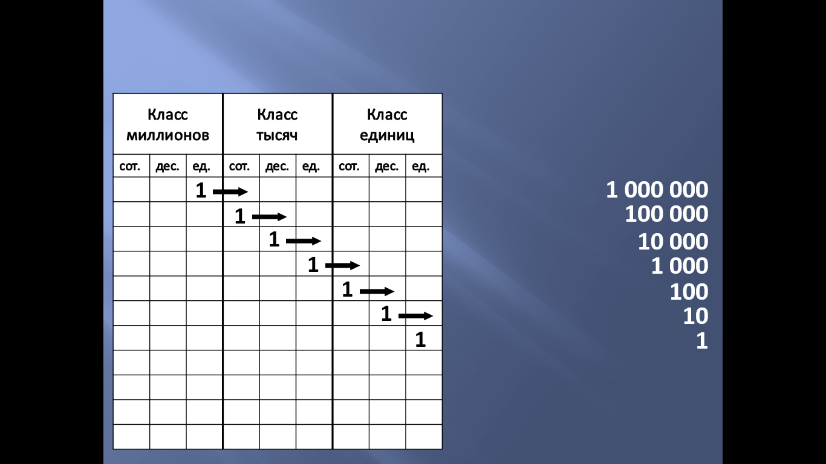

1. Мотивационный этап:

Цель: способствовать возникновению интереса у обучающихся к понятию «десятичная дробь», сформулировать тему и цель урока.

Вид: возбуждение интереса учащихся к изучению понятия «десятичная дробь».

Прием: историческая справка.

Ход:

Учитель: Ребята, оказывается дроби, у которых в знаменателе находится разрядная единица, можно записать по-другому: короче и проще. Эта запись будет называться десятичной записью дробных чисел или десятичной дробью.

Историческая справка:

Уже несколько тысячелетий человечество пользуется дробными числами, а вот записывать их удобными десятичными знаками оно додумалось значительно позже.

В начале XV века математик и астроном аль-Коши из Самарканда (Узбекистан) стал пользоваться десятичными дробями и в своей книге "Ключ к арифметике" сообщает правила умножения и деления таких дробей. Европейцам этот труд был не известен, и пришлось изобретать десятичные дроби заново.

Лишь в конце XVI века мысль записывать дробные числа десятичными знаками пришла некоему Симону Стевину из Фландрии (теперь Бельгии). В своей книге "Десятая" он не только излагает теорию десятичных дробей, но и старается убедить людей пользоваться ими, говоря, что при их использовании "изживаются трудности, распри, ошибки, потери и прочие случайности, обычные спутники расчетов".

Учитель: Вы все, наверно, уже догадались какая тема будет на сегодняшнем уроке.

Дети: Десятичная запись дробных чисел.

Учитель: Молодцы! Запишите, пожалуйста, тему сегодняшнего урока в тетраде. А какова будет цель нашего урока?

Дети: Научиться записывать обыкновенные дроби в знаменателе которых находится разрядная единица в виде десятичной дроби.

1. Ориентировочный этап:

Цель: познакомить с понятием «десятичная дробь», научить читать десятичные дроби, записывать обыкновенную дробь и смешанное число в виде десятичной дроби и десятичную дробь в виде обыкновенной дроби или смешанного числа.

Метод: частично-поисковый.

1. Этап введения понятия десятичной дроби.

Цель: ввести понятие «десятичная дробь».

Способ: конкретно-индуктивный.

Ход:

Учитель: Итак, давным-давно математики договорились о том, чтобы обыкновенные дроби, у которых в знаменателе стоит разрядная единица писать по-другому, попроще и покороче. Решили, что будут писать только целую часть и числитель обыкновенной дроби. А чтобы их как-то разделять, договорились ставить между ними запятую. Читается десятичная запись числа точно так же, как и само смешанное число – пять целых четыре десятых. Как вы видите знаменатель дроби обязательно проговаривается. А как же, не написав знаменателя, по виду десятичной дроби определить его.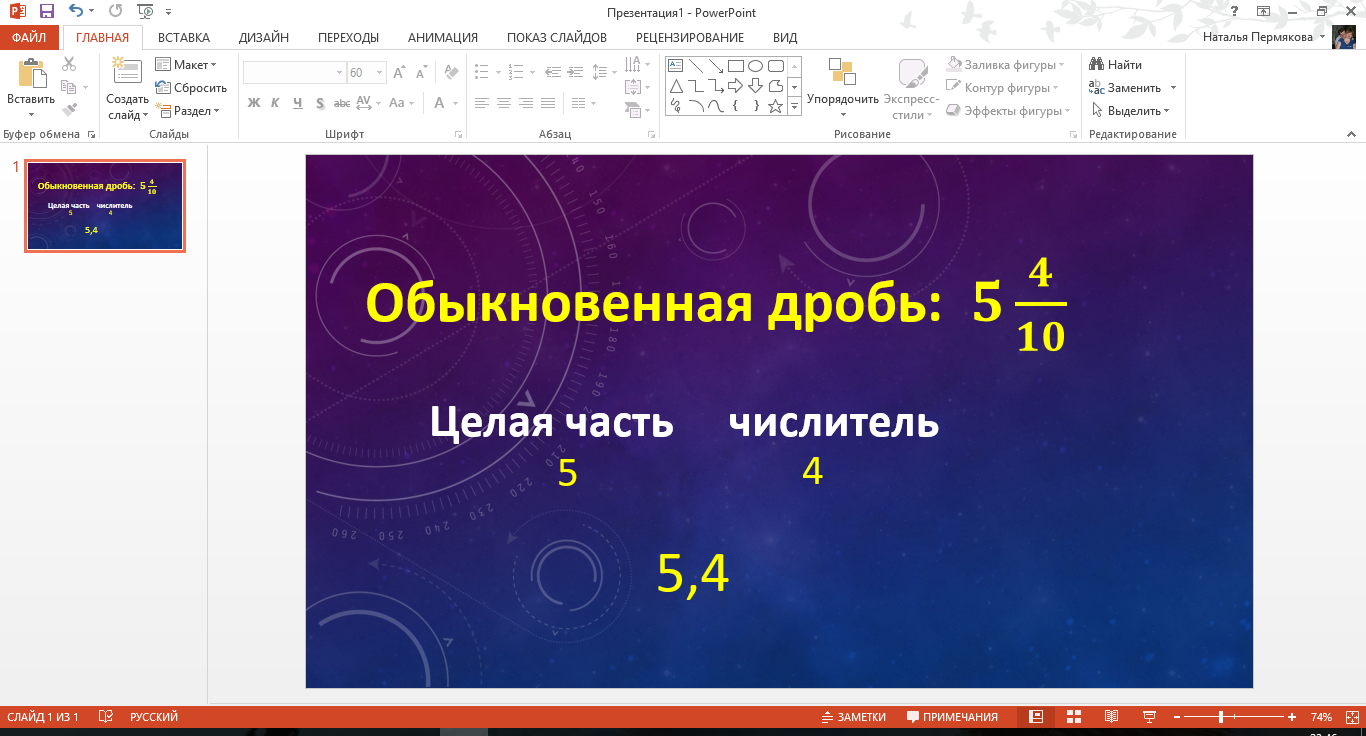

Учитель: Существует правило, число цифр после запятой и число нулей у разрядной единицы должно быть одним и тем же! Посмотрим на пример выше.

Учитель: Сколько нулей у единицы в знаменателе?

Дети: Один.

Учитель: Сколько цифр после запятой в десятичной дроби?

Дети: Одна.

Учитель: Правило выполняется?

Дети: Да. Хорошо.

Учитель: Давайте запишем число 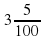в виде десятичной дроби. Для этого мы должны записать только целую часть и числитель, отделив их друг от друга запятой. Но помним правило! Число нулей в знаменателе обыкновенной дроби и число цифр после запятой должно быть одно и то же! То есть нуля в знаменателе два, значит и после запятой должно быть 2 цифры. Нам на помощь придет «0». Надо приписать «0» к «5». А здесь давайте подумаем: с какой стороны можно дописать 0, чтобы число не изменилось?

Дети рассуждают: Если припишем ноль справа – получим число 50, но 5 и 50 это разные числа, значит писать ноль справа нельзя! Теперь давайте напишем 0 слева. Получим число 05, оно равно 5.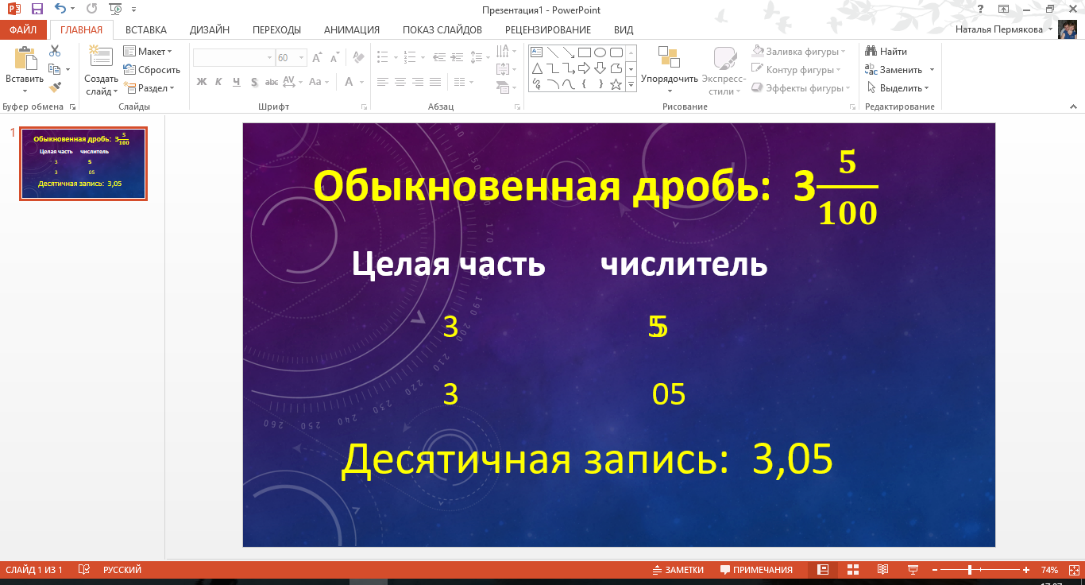

Учитель: Значит смешанное число 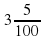можно записать по-другому: 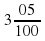. Теперь количество цифр в числителе равно количеству нулей в знаменателе. Теперь сможем записать это число в десятичном виде?

Дети: Да, сможем.

Учитель:Как будет выглядеть десятичная запись?

Дети: 3,05.

1. Этап формирования ведущего действия

Цель: сформировать умение записывать обыкновенные дроби и смешанные числа в виде десятичных дробей.

Метод: объяснительно-иллюстрационный.

Ход:

Учитель: Составим алгоритм действий, с помощью которого мы будем записывать обыкновенную дробь в десятичном виде, т.е. с помощью запятой.

Алгоритм

1. Определить целую часть смешанного числа -

   

2. Определить числитель дробной части –

3. Сравнить количество цифр в числителе и количество нулей в знаменателе:

а) если одинаково – перейти к пункту 4.

б) если количество разное - уравнять количество цифр в числителе и количество нулей в знаменателе, приписав к числителю нули слева.

1. Записать целую часть и преобразованный числитель рядом, отделив их запятой.

Учитель: Давайте попробуем, используя этот алгоритм записать несколько обыкновенных дробей в десятичном виде:

Пример 1: :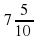

1. Целая часть – 7

2. Числитель – 5

3. А)

4. 7,5

Пример 2: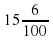

1. Целая часть – 15

2. Числитель – 6

3. Б) 06

4. 15,06

Пример 3: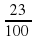

1. Целая часть – 0

2. Числитель – 23

3. А)

4. 0,23

1. Этап формирования других действий, связанных с понятием.

Цель: Сформировать умение записывать неправильные дроби в десятичном виде, записывать десятичную дробь в виде обыкновенной дроби или смешанного числа, читать десятичные дроби, распознавать десятичные дроби.

Метод: репродуктивный.

Ход:

Учитель: Ребята, до этого момента мы записывали в десятичном виде только смешанные числа и правильные дроби. Давайте посмотрим, как можно записать в десятичном виде неправильную дробь с разрядной единицей в знаменателе.

Пример 1.

Учитель: Запишем в виде десятичной дроби число 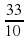. Чтобы записать целую часть числа надо ее сначала выделить из неправильной дроби: 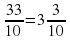. Дальше действуем по алгоритму: целая часть – 3, числитель – 3, количество цифр в числители и количество нолей в знаменателе одинаково, поэтому пишем целую часть и числитель через запятую – 3,3.

Пример 2.

Учитель: Еще один пример: запишем в десятичном виде число дробь 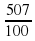. Определяем, что дробь неправильная, выделяем целую часть: 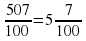. Записываем целую часть и числитель дроби через запятую, учитывая, что количество цифр после запятой и количество нулей в знаменателе должно быть одинаково: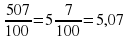

Учитель: Ребята, не всегда в матиматике требуется переписывать обыкновенную дробь в десятичном виде, иногда нужно сделать обратное: записать десятичную дробь в виде обыкновенной дроби. Давайте попробуем.

Пример 3.

Запишем в виде обыкновенной дроби десятичную дробь 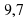. Мы знаем, что для записи десятичной дроби используют целую часть и числитель обыкновенной дроби: значит целая часть равна 9, а числитель раввен 7. Остается определить знаменатель: 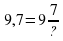. Мы знаем, что в знаменателе должна быть единица с таким количеством нулей, сколько цифр в числителе. Здесь числитель состоит из одной цифры – значит у единицы 1 ноль.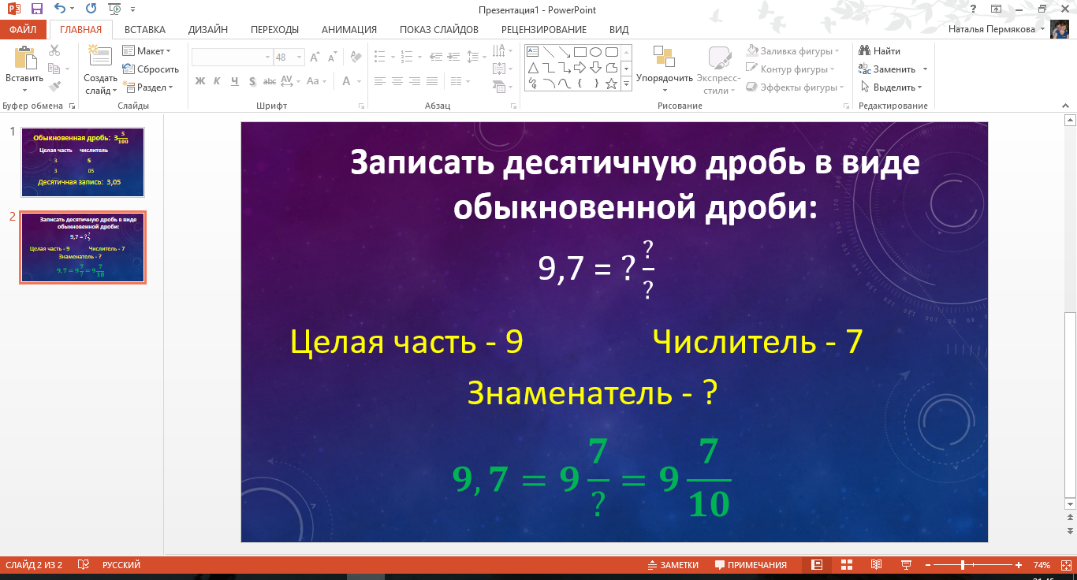

Значит: . (Слайд)

И еще раз хочу напомнить, что одна и та же дробь, записанная в разном виде, поэтому и читается она одинаково!

Учитель: Прочитайте следующие десятичные дроби слайд):

6,7; 13,1; 8,07; 0,25; 45,015; 607,0002; 2,00458.

Дети: (читают вслух числа)

Учитель: Хорошо, ребята, если десятичная дробь и обыкновенная одинаково читаются, то как их отличить друг от друга по виду?

Дети: Обыкновенная дробь записывается с помощью дробной черты, а десятичная – с помощью запятой.

Учитель: Запишите числа, записанные на доске по столбикам: в первый столбик запишите натуральные числа, во второй столбик обыкновенные дроби и смешанные числа, в третий столбик десятичные дроби:

Дети:

Дети:

1. Этап обучения применению понятия «десятичная дробь».

Цель: закрепить умение записывать обыкновенные дроби в десятичном виде и десятичной дроби в виде обыкновенной дроби или смешанного числа, читать десятичные дроби.

Метод: репродуктивный

Ход:

Учитель: Теперь я буду называть числа, а вы будете их записывать в виде десятичных дробей: (дублируется учениками у доски)

- пять целых 8 десятых (5,8)

- тринадцать целых тринадцать сотых (13,13)

- ноль целых сорок семь тысячных (0,047)

- девяносто девять целых пять сотых (99,05)

- триста двадцать шесть целых пять тысяч сто шесть десятитысячных (326,5106)

- сорок одна целая две милионных (41,000002)

Учитель: Ребята, а теперь у доски решим № 1144 из учебника (5 примеров):

Вам в помощь я раздала карточки, которые вам помогут себя проверить. В них разряды чисел, но теперь не только целой части, но и дробной.

Дети: (решают у доски, проговаривая каждое действие по алгоритму, читают полученную дробь)

; ;

;

;

; ; ; ;

;

Учитель: Молодцы, теперь решим № 1147 (ученики по очереди решают у доски, читая десятичные дроби и проговаривая процесс их записи в виде обыкновенных дробей)

; ; ; ;

; ; ; ; .

1. Домашнее задание:

№ 1146, 1149.

1. Рефлексия (подведение итогов урока)

Ребята, заканчивая наш урок, подведем итоги:

Учитель: Какую цель мы ставили в начале урока?

Дети: Научиться записывать обыкновенные дроби в знаменателе которых находится разрядная единица в десятичном виде

Учитель: Достигли ли мы поставленной цели?

Дети: Да, достигли.

Учитель: Какие еще математические действия мы научились выполнять на этом уроке?

Дети: Научились записывать десятичные дроби.

Учитель: Что осталось непонятым на уроке? (?)

Учитель: Поднимите руки те, кто теперь умеет записывать обыкновенные дроби с разрядной единицей в знаменателе в виде десятичной дроби.

Учитель: Поднимите руки те, кто умеет записывать десятичные дроби в виде обыкновенной дроби?

Учитель: Молодцы!!! Урок окончен.

4