3
Тема урока «Делимость произведения»
Цель урока: создать условия для «открытия» формулировки признака делимости произведения на число
Задачи урока:
Обучающие: вырабатывать умения и навыки применения признака делимости произведения на число при решении задач
Развивающие: формировать у учащихся логическое мышление, культуру математической речи, умение аргументировать свои выводы
Воспитательные: формировать навыки самостоятельной работы, доброжелательное отношение друг к другу, умение выполнять самоконтроль и самооценку своих учебных действий
Структура урока:
Организационный момент
Актуализация опорных знаний
Формулировка темы. Постановка цели урока.
Изучение нового материала
Физкульминутка
Первичное закрепление материала
Закрепление изученного в процессе решения задач
Подведение итогов урока, рефлексия
Домашнее задание
Организационный момент
Актуализация опорных знаний учащихся
Эпиграф урока: «Числа правят миром»
«Все вещи можно представить в виде чисел», - говорил древнегреческий ученый и философ Пифагор. Таким образом, он давал понять, что миром правят числа и за каждым числом прячется тайна. Пифагор считал, что через число можно выразить все закономерности мира. Сегодня на уроке с помощью чисел мы тоже попробуем выявить некоторую закономерность
Давайте вспомним, какие новые понятия были изучены на предыдущих уроках?
Дайте определение понятиям: кратное, делитель.
Более подробно вспомним - делитель и кратное.
Математический диктант
Укажите все делители числа 18; 45.
Из чисел 3,6,10,22,17,30,120 выберите те, которые являются
делителями числа 60; 66.
Какие из чисел 15,25,100,300 кратны 20?
Назовите несколько кратных 16.
Формулировка темы. Постановка цели урока.
Выполним задания учебника № 740 – 742 (стр. 167).
Как вы думаете, что мы попытаемся выяснить сегодня на уроке?
Тема урока – ДЕЛИМОСТЬ ПРОИЗВЕДЕНИЯ
В тетрадях запишем тему урока: «Делимость произведения»
Цель урока: Научиться определять делится ли произведение чисел на данное число или нет
Задачи урока:
Получить правило делимости произведения на данное число
Научиться применять его при решении задач
1
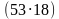 делится 3;
делится 3;
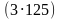 делится 25;
делится 25;
(21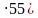 делится 77.
делится 77.
4. Изучение нового материала
- Сейчас мы с вами постараемся сформулировать правило, по которому будем определять - делится произведение на некоторое число или нет. Для этого выполним работу в парах (по рядам).
Работа в парах
1)Заполните таблицу:
| Произведение чисел делится на 3? | Произведение чисел делится на 3 (приведите примеры) | Произведение чисел не делится на 3 (приведите примеры) |
| 7 ∙ 11 = |
|
|
| 21 ∙ 8 = |
|
|
| 2 ∙ 29 = |
|
|
| 23 ∙24 = |
|
|
| 18 ∙ 6 = |
|
|
| Произведение чисел делится на 5? | Произведение чисел делится на 5 (приведите примеры) | Произведение чисел не делится на 5 (приведите примеры) |
| 7 ∙ 20 = |
|
|
| 24 ∙ 8 = |
|
|
| 15 ∙ 45 = |
|
|
| 35 ∙ 49 = |
|
|
| 19 ∙ 6 = |
|
|
| Произведение чисел делится на 7? | Произведение чисел делится на 7 (приведите примеры) | Произведение чисел не делится на 7 (приведите примеры) |
| 56 ∙ 11 = |
|
|
| 22 ∙ 8 = |
|
|
| 12 ∙42 = |
|
|
| 14 ∙ 42 = |
|
|
| 17 ∙ 6 = |
|
|
2) Постарайтесь сформулировать правило деления произведения на число 3(5, 7) из рассмотренных примеров:
Если……………………………..делится на число …, то и произведение ………………
3) Постарайтесь сформулировать правило деления произведения на некоторое число:
| Если…………………………………..делится на некоторое число …, то и произведение ……………………… |
Докажите предположение, заполняя следующие пропуски
4) Дано произведение 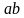 , причем
, причем 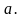
Докажем, что произведение 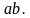
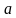 , значит, существует такое натуральное число k, что
, значит, существует такое натуральное число k, что 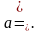
Тогда 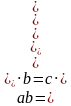 , где
, где 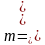 ,
,
 – натуральное число.
– натуральное число.
Значит, существует такое натуральное число , что
, что 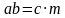 . Следовательно, произведение
. Следовательно, произведение 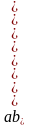 .
.
Дано произведение 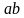 , причем
, причем 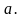
Докажем, что произведение 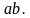
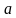 , значит, существует такое натуральное число k, что
, значит, существует такое натуральное число k, что 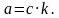
Тогда 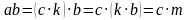 , где
, где 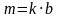 ,
,
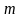 – натуральное число.
– натуральное число.
Значит, существует такое натуральное число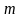 , что
, что 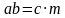 . Следовательно, произведение
. Следовательно, произведение 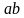 нацело делится на с.
нацело делится на с.
- Данное утверждение называется признаком делимости (см. стр. 169 учебника) – дома записать в тетрадь для правил
Физкультминутка
Быстро встали, улыбнулись,
Выше-выше подтянулись.
Ну-ка плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали, сели, встали,
И на месте побежали.
А теперь вздохнули дружно.
Нам урок продолжить нужно.
Подравнялись, тихо сели
И в тетрадки посмотрели.
6. Первичное закрепление материала
Выполним устно задание № 743 (стр. 743)
Остановимся подробно на пункте 5.
Произведение – делится на 10?
Произведение – делится на 10?
Приведите примеры, когда ни один из множителей не делится на некоторое число, а произведение делится на это число.
Приведите примеры, когда ни один из множителей не делится на некоторое число и произведение не делится на это число.
7. Закрепление изученного в процессе решения задач
Не выполняя вычислений, покажите, что произведение делится на 4.
Образец:
Вернемся к выполнению заданий № 740 – 742.
а) покажите, что произведение делится на 3;
б) покажите, что произведение кратно 25;
в) покажите, что произведение 21 кратно 77.
3) Выполним задание № 744 (а, б) по рядам (со взаимопроверкой)
(проверить 2 работы), в это время у доски ученик выполняет задание
№ 744(в)
4) Выполните задание № 747(а)
Покажите, что данную дробь можно сократить на 9.
Образец:
Подведение итогов урока, рефлексия
Цель урока: Научиться определять делится ли произведение чисел на данное число или нет
Какие задачи с вами решили на этом уроке?
Получили правило делимости произведения на данное число
Научились применять его при решении задач
Домашнее задание
п. 26, выучить признак делимости произведения на некоторое число.
№ 744(г), 747(б), 755(а-в)

 Получите свидетельство
Получите свидетельство Вход
Вход











 Конспект урока "Делимость произведения" (46.81 KB)
Конспект урока "Делимость произведения" (46.81 KB)
 0
0 302
302 13
13 Нравится
0
Нравится
0







