Открытый урок по теме «Методы решения иррациональных уравнений»
11 класс
| Методическая информация | ||||||||||
| Тип урока | Урок обобщения и систематизации знаний | |||||||||
| Цели урока
| Цель урока: обобщение и систематизация способов решения иррациональных уравнений, формирование у учащихся способностей к самостоятельному построению новых способов решения более сложных типов иррациональных уравнений. | |||||||||
| Задачи урока | образовательные: выработать алгоритмы решения различных видов уравнений, правильно отбирать способы решения рассмотреть примеры иррациональных уравнений в том числе и при выполнении заданий ЕГЭ. развивающие: • развитие внимания, памяти, умения рассуждать и аргументировать свои действия через решение проблемной задачи; • развитие познавательного интереса к предмету; • формирование эмоционально-положительного настроя у учащихся путем применения активных форм ведения урока; • развитие рефлексивных умений через проведение анализа результатов урока и самоанализа собственных достижений. воспитательные: • развитие коммуникативных умений учащихся через организацию групповой, фронтальной работы на уроке. | |||||||||
| Используемые педагогические технологии, методы и приемы | Применяемая технология: технология деятельностного метода обучения Методы организации работы: - словесные методы (беседа, чтение), - наглядные (интерактивная доска), - проблемно-поисковый, -метод рефлексивной самоорганизации (деятельностный метод). Формы организации работы: - групповая, - коллективная (фронтальная), - индивидуальная. | |||||||||
| Время реализации урока | Третий урок по теме «Иррациональные уравнения» | |||||||||
| Знания, умения, навыки и качества, которые актуализируют/приобретут/ закрепят/др. учащиеся в ходе урока | Знания, умения, навыки: Учащиеся должны знать и уметь применять свойства арифметического корня, решать квадратные уравнения. - ясно, точно, грамотно излагать свои мысли в устной и письменной речи, использовать различные языки математики (словесный, символический), свободно переходить с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства; - проводить доказательные рассуждения, аргументировать, выдвигать гипотезы и их обосновывать; - осуществлять поиск, систематизировать, анализировать и классифицировать информацию, использовать информационные источники, включая учебную литературу. Перечень универсальных учебных действий: - личностные (Л), - коммуникативные (К), - познавательные (общеучебные и логические) (П), - регулятивные (Р). | |||||||||
| Необходимое оборудование и материалы | Компьютер, проектор, интерактивная доска. | |||||||||
| Дидактическое обеспечение урока | - компьютерная презентация, - карточки с заданиями, - карточки с практическим заданием по теме. | |||||||||
| Список учебной и дополнительной литературы | Алгебра и начала математического анализа: Учебник для 11 кл. базовый уровень/ Колмогоров А. Н., М.: Просвещение, 2010. | |||||||||
| Ход и содержание урока деятельность учителя и учеников | ||||||||||
| 1. Самоопределение к деятельности Цели для преподавателя: - создание условий для возникновения у учащихся внутренней потребности включения в учебную деятельность («хочу»); -установление тематических рамок («могу»). Для учащихся: -включение в учебную деятельность. | Здравствуйте ребята и гости! Наш урок я хочу начать притчей: «Однажды молодой человек пришел к мудрецу. Каждый день по пять раз я произношу фразу: «Я принимаю радость в мою жизнь, но радости в моей жизни нет». Мудрец положил перед собой ложку, свечу и кружку и попросил: «Назови, что ты выбираешь из них». «Ложку» - ответил юноша. «Произнеси это 5 раз». Я выбираю ложку» - послушно произнес юноша 5 раз. «Вот видишь» - сказал мудрец, «повторяй хоть миллион раз в день, она не станет твоей. Надо…» «Что же надо?» Надо протянуть руку и взять ложку. Вот и вам сегодня надо взять свои знания и применить их на практике. Слайд № 2. Слайд № 3. Эпиграфом к нашему уроку станут слова С. Коваля: «Уравнения – это золотой ключик, открывающий все математические сезамы». То есть другими словами можно сказать, что если вы будете уметь решать уравнения, то экзамена по математике вам не стоит бояться. Посмотрите на уравнения. Как они решаются? Давайте их решим. Запишите в тетрадях число, классная работа, пустая строка – тема урока. Минутка знаний: Слайд № 4 Решить уравнения: (Три человека решают на доске). х2-24=-5х (-8;3)
Последнее уравнение отличается от первых двух. Чем? Каким методом мы его решили? | |||||||||
| 2. Актуализация теоретических знаний Цели для преподавателя: -актуализация изученных способов действий, достаточных для построения нового знания, их обобщение и знаковая фиксация; -актуализация соответствующих мыслительных операций и познавательных процессов; -мотивирование учащихся к пробному учебному действию и его самостоятельное осуществление. Для учащихся: -фиксирование индивидуальных затруднений в выполнении пробного учебного действия или его обосновании. | Преподаватель: -Каким еще методом мы решали иррациональные уравнения? (Методом введения новой переменной или метод подстановки) Преподаватель: Сейчас вам предлагается решить ещё 1 иррациональное уравнение методом подстановки: Слайд № 5
На доске 1 человек решение. Ответ: 64 Преподаватель: Какое из двух иррациональных уравнений вызывает наибольшие затруднения? (предполагаемый ответ учащихся – 2)
Как вы думаете какова будет тема нашего урока? | |||||||||
| 3.Постановка учебной задачи. Цели для преподавателя: -создание условий для постановки учебной задачи. Для учащихся: -выявление места и причины затруднения, постановка цели урока
| Слайд № 6 Методы решения иррациональных уравнений. Преподаватель: запишем тему урока на доске и в тетрадях. Слайд № 7. И цель нашего урока - систематизация методов решения иррациональных уравнений, решение более сложных типов иррациональных уравнений. Сегодня именно знание методов решения иррациональных уравнений станет для нас теми кирпичиками, с помощью которых мы сможем решать более сложные уравнения.
| |||||||||
| 4. Групповая работа Цели для учащихся: -выбор способа решения учебной задачи; -выдвижение и обоснование гипотезы. Для преподавателя: - создание условий для фиксирования в речи учащихся и знаково нового способа действий, помогает найти правильный путь решения. | Преподаватель: А сейчас предлагается работа по группам. Я приготовила для вас карточку - информатор, чтобы вы воспользовавшись ею, смогли решить, предложенные вам уравнения. Время ____ Задание. Решите уравнения методом введения новой переменной: Слайд № 8
Ответы: на экране. Слайд № 9 2 84 630 (идёт работа в группах, сверка ответов с доской, проходит общее обсуждение и делается общий вывод). Преподаватель дает рекомендации по ходу обсуждения. Преподаватель: У доски один учащийся предлагает своё решение из любой группы. Класс принимает участие, по необходимости задают вопросы. Остальные 2 решения появляются на слайде. Слайды № 10, 11,12 1.Введём новую переменную. Пусть По условию подходит а =1. 2.Введём новую переменную. Пусть По условию подходит а =3. 3.Введём новую переменную. Пусть По условию подходит а =5. Давайте еще раз сделаем общий вывод: вспомним алгоритм решения иррациональных уравнений введением новой переменной. Слайд № 13 Алгоритм решения методом введения новой переменной: Введём новую переменную Решим полученное уравнение Найдём значение искомой переменной Выполним проверку. Преподаватель обобщает: итак, вы вспомнили основные методы решения иррациональных уравнений, которые обогатили ваш математический арсенал. В каждом методе есть свои тонкости, о которых надо помнить. Физминутка. (Музыка). Слайд № 14 (Карточки крупным шрифтом) Если уравнение линейное – руки вверх, если – квадратное – приседаем, если иррациональное – руки на поясе.
Х2-14х+48=0
Х2-11х+30=0
Х2-9х+20=0 -
| |||||||||
| 5. Первичное закрепление Цели для преподавателя: -создание условий для первичного закрепления. Для учащихся: -усвоение нового способа действий. | Преподаватель: Давайте решим ещё одно уравнение. Обратите внимание на столах другого цвета карточки – информаторы, которые вам помогут. Слайд № 15. Выполнить задание из учебника № 425 (б) с комментарием у доски: Слайд № 16 2
тогда
(один учащийся озвучивает решение у доски с обязательным проговариванием вслух правила) | |||||||||
| 6. Включение в систему знаний и повторение. Цели для преподавателя: -создание условий для включения «открытия» в систему знаний, повторение и закрепление ранее изученного. Для учащихся: -включение «открытия» в систему знаний, повторение и закрепление ранее изученного. | Преподаватель: Конечно, недостаточно просто научиться решать иррациональные уравнения. Необходимо знать, где их можно ещё применить. Рассмотренные сегодня примеры взяты из экзаменационных заданий ЕГЭ. А сейчас вам предлагается разобрать задачу, в которой полученные сегодня знания пригодятся для практического применения. Решаем задачу, 1 человек выходит к доске. Слайд 17, 18 Решить задачу: При движении ракеты её видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону , где Решение Найдём, при какой скорости длина ракеты станет равной 4м. Задача сводится к решению уравнения . Длина покоящейся ракеты Скорость света с=3 5 =4; = 1 - V=180000км/c. Решение. Найдем, при какой скорости длина ракеты станет равна 4 м. Задача сводится к решению уравнения при заданном значении длины покоящейся ракеты
км/с. Если скорость будет превосходить найденную, то длина ракеты будет менее 4 метров, поэтому минимальная необходимая скорость равна км/с. Ответ: 180 000. Ответ: 180000
| |||||||||
| 7. Самостоятельная работа в форме ЕГЭ с заполнением бланка | На экзамене вам придется ответы записывать в бланк. Давайте выполним задание и занесём в бланк ответы. Каждый учащийся берет свой бланк, заранее подписанный. Время _____ Слайд 19 № 1. Решите уравнения. Установите соответствие. 1. 2. 3. 4.
№ 2. Найдите сумму корней уравнения:
№ 3. Какому из промежутков принадлежат корни уравнения:
(-1;2) (2;4) № 4. Найдите среднее арифметическое корней уравнения:
№ 5. Решить уравнение:
Ответы: Слайд № 20 4312 -2 1 -1,5 -3;3 | |||||||||
| 8. Рефлексия учебной деятельности на уроке (итог урока) Цели для преподавателя: -создание условий для рефлексии учебной деятельности учащихся на уроке. Для учащихся: -самооценка результатов деятельности; -осознание метода построения, границ применения нового знания.
Задание для самоподготовки | Преподаватель: Сегодня мы с вами попытались обобщить и углубить знания по теме: Методы решения иррациональных уравнений» с целью качественной подготовки к ЕГЭ. Надеюсь, что урок вам понравился. Слайд № 21 Проведём самооценку результатов своей деятельности, ответив на вопрос: Такие уроки помогут мне: -с лёгкостью сдать базовый уровень ЕГЭ -быть уверенным на экзамене -проверить свои знания 2) Мое настроение: -стало лучше - стало хуже
Слайд № 22 Учебник № 425 (г), Сборник 4000 задач стр. 529 № 3366 | |||||||||
|
| Слайд № 23. Давайте вернемся к эпиграфу нашего урока (на доске - эпиграф): «Уравнения – это золотой ключик, открывающий все математические сезамы». Мне хотелось бы вам пожелать, чтобы каждый из вас нашел в жизни свой «золотой ключик», с помощью которого перед вами открывались бы любые двери. Всем спасибо за работу! | |||||||||

 Получите свидетельство
Получите свидетельство Вход
Вход



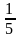 х2-5=0 (-5;5)
х2-5=0 (-5;5)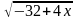 =2 (Оставить решение на доске) (9)
=2 (Оставить решение на доске) (9)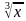 -
- 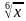 = 2;
= 2; 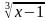 +2
+2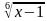 =3
=3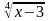 + 6 –
+ 6 – 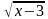 = 0;
= 0;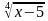 = 30-
= 30- 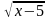
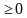 , тогда
, тогда 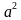 =0. Корни: -3 и 1.
=0. Корни: -3 и 1.








 Конспект урока алгебры в 11 классе "Методы решения иррациональных уравнений" (74.95 KB)
Конспект урока алгебры в 11 классе "Методы решения иррациональных уравнений" (74.95 KB)
 0
0 539
539 101
101 Нравится
0
Нравится
0


