Школа: КГУ « Школа-гимназия №10» акимата города Рудного
Учитель: Кирдина Татьяна Васильевна
Предмет: алгебра и начала анализа
Тема урока: Решение логарифмических уравнений .
Цель урока: Обеспечить усвоение учащимися темы «Логарифмические уравнения»
Обучающие: систематизация знаний учащихся по теме «Решение логарифмических уравнений»
Развивающие : способствование формированию умений применять полученные знания в новой ситуации, развитие навыков самопроверки и самооценки, навыков работы в группах .
Воспитывающие: воспитание интереса к математике , активности, мобильности; Формирование навыков адекватной самооценки деятельности.
Эпиграф урока
«Величие человека - в его способности мыслить».
Б. Паскаль
Ход урока:
Организационный момент.
На каждом этапе урока учащиеся будут самостоятельно, работая индивидуально или в группах, оценивать свои знания с помощью рейтинговых баллов, выставляя их в рейтинговые листы.
Рейтинговый лист
Тема: "Решение логарифмических уравнений"
Группа №1. Консультант:_____________________
|
№ п/п |
Ф.И. учащегося | Домашняя работа (учебный проект) |
Устные упражнения | Решение логарифмических уравнений | Работа по группам (решение уравнений) |
Тест | Общее кол-во баллов |
| Рейтинговый балл | 5-10 | 1 | 2 | 2-12 | 5-9 |
|
| 1. |
|
|
|
|
|
|
|
| 2. |
| |
|
|
|
|
|
| 3. |
|
|
|
|
|
|
|
| 4. |
|
|
|
|
|
|
|
| 5. |
|
|
|
|
|
|
|
|
Оценка | "3" "4" "5" | 30-39б 40-49 б 50-55 б |
|
II. Проверка домашнего задания.
Класс предварительно был разбит на 4 группы, в каждую входят учащиеся с разным уровнем обученности: I уровень – базовый, II уровень – повышенный (по сравнению с базовым), III уровень – высокий.
Каждая группа учащихся должна представить один из методов решения уравнений (теория) и подобранные из материалов ЕНТ уравнения разного уровня, при решении которых использовался один из выбранных методов:
I метод. Метод использование определения логарифма
II метод. Метод разложения на множители.
III метод. Метод введения новой переменной.
IV метод. Метод потенцирования.
Работа выполнена в виде учебных проектов с презентацией. Учащиеся оценивают свою работу в группе (самооценка, взаимооценка), выставляют баллы в рейтинговый лист.
Предложенные уравнения:
1 группа.
III метод (метод введения новой переменной).
lg2 x3 - 10lgx + 1=0
Приведём уравнение к квадратному:
Т.к. lg2 x3=(lgx3)2=(3lgx)2= 9lg2 x, то
9lg2 x - 10lgx+1=0.
Пусть lg x=y, тогда 9y2- 10y+1=0; D=64
y=1 или y=1/9
lgx=1 или lgx=1/9
x=10 или х=10 1/9.
Проверкой подтверждаем, что оба числа являются
корнями.
Ответ: 10; 10 1/9
.
2 группа.
I метод (метод использования определения логарифма).
log х+1(2x2+1)=2
По определению логарифма имеем: 2х2+1=(х+1)2,
X2 -2x=0
x=2 или x=0.
Проверка:
х=0 не может быть корнем данного уравнения, так как основание логарифма х+1≠1.
При х=2 log 2+1( 2•22 +1)=log39=2.
Ответ: 2.
III. Устные упражнения (по 1 баллу – за верное решение).
1Найдите значение выражения: Решите уравнение:
|
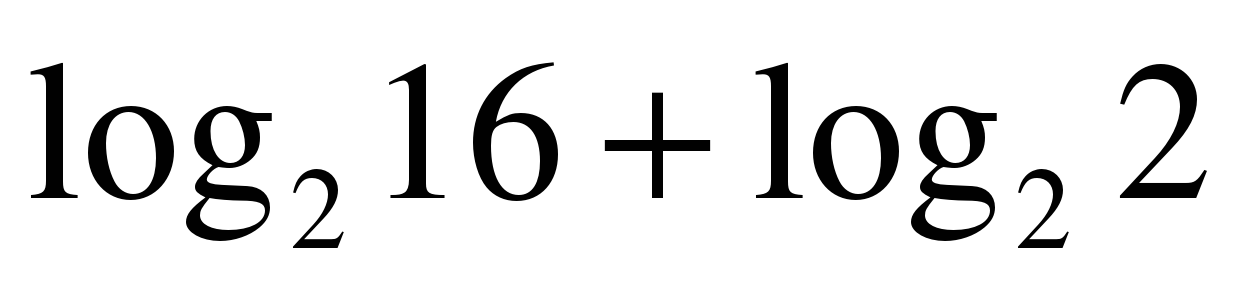 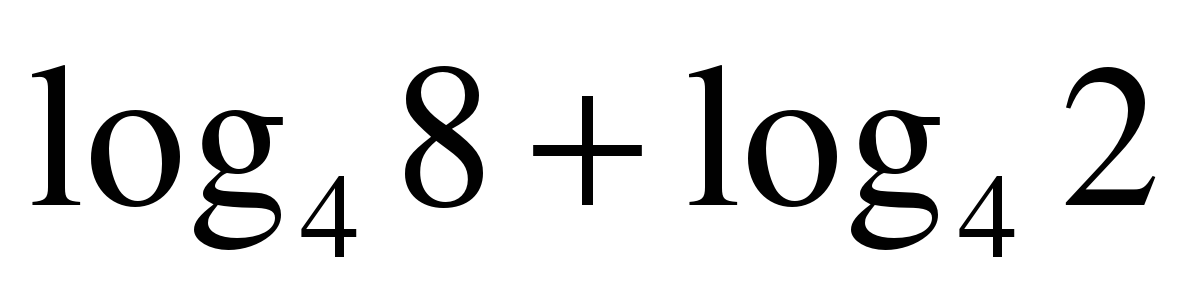 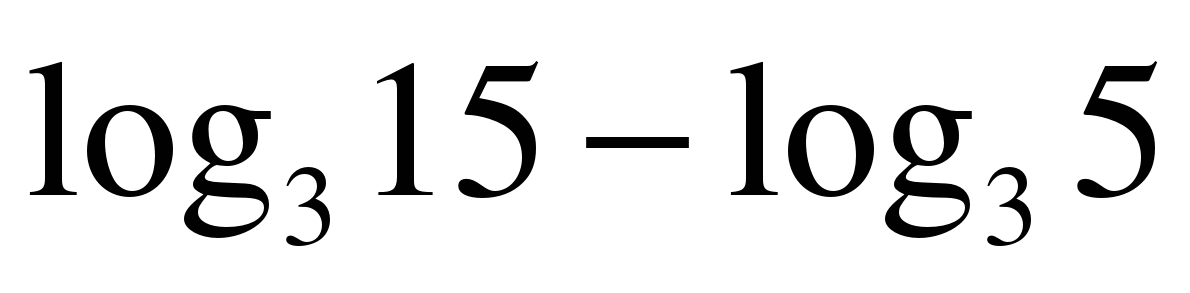 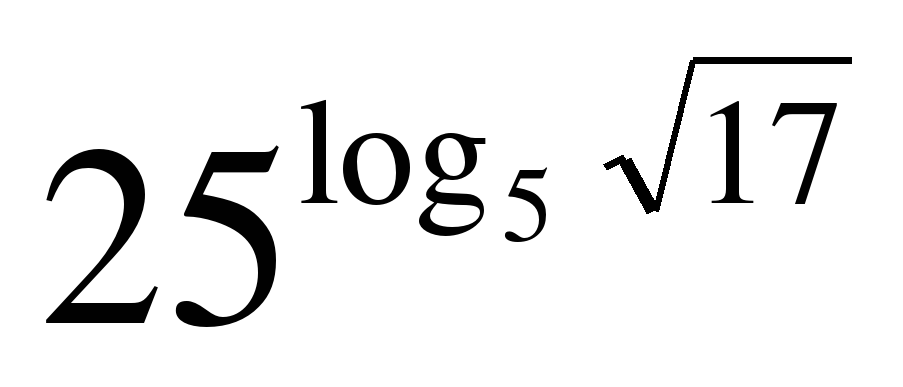
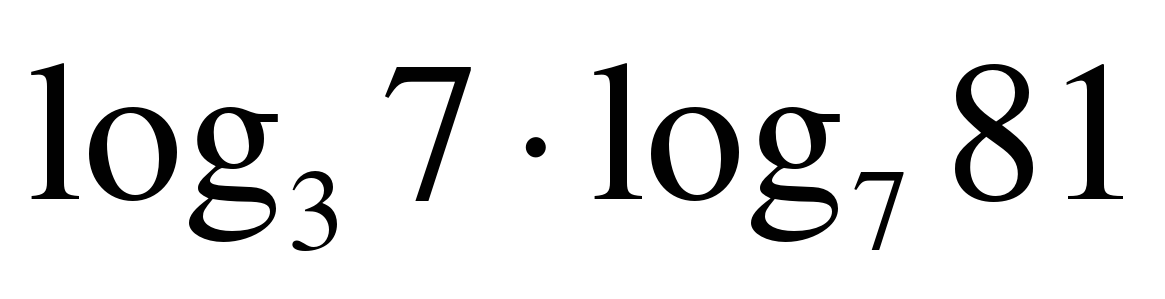
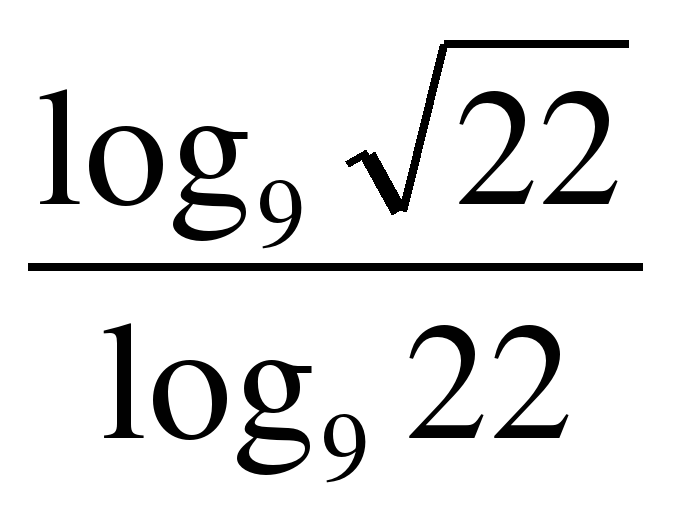
| log3x=4 log2(x+1)=3 logх16=2 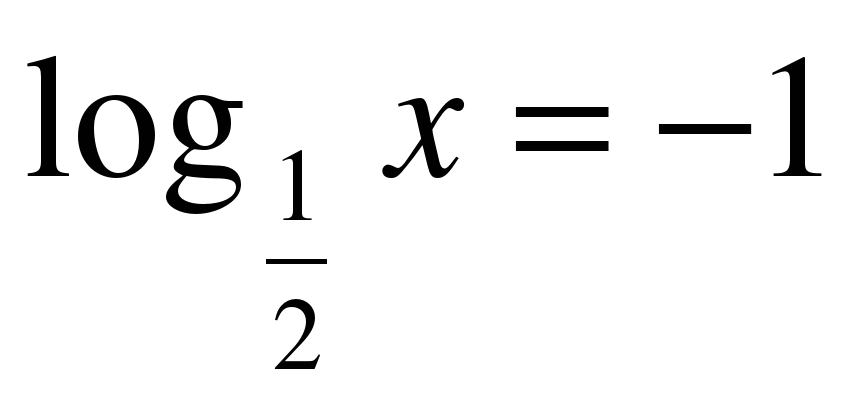 log3x=-3 log2(x-5)=-2
|
Актуализация базовых знаний
Решая уравнения, необходимо указать метод решения. ( по 2 балла за верное решение уравнений)
1) Укажите корень уравнения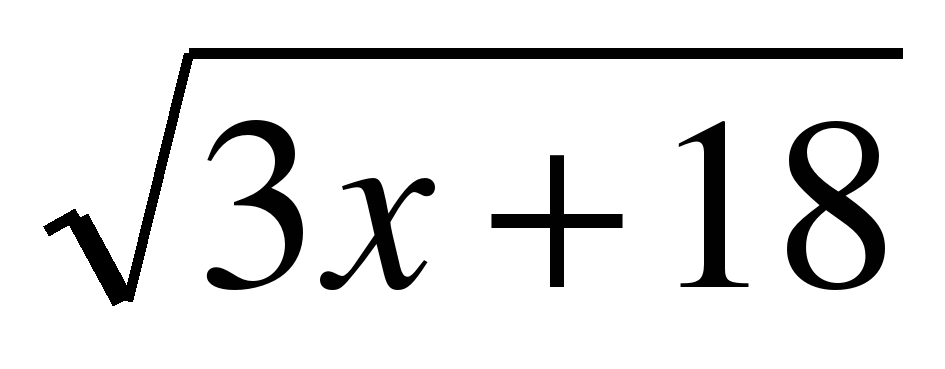 log4(4-х)=0
log4(4-х)=0
Ответ: х =-6; х=3 II метод.
2) Решите уравнение log3x + log3(x + 3) = log3(x + 24),
Ответ: х =4; I метод.
3) Решите уравнение lg (x+ 7) – lg (x+ 5) = 1.
Ответ: х=0; IV метод.
Решить уравнение ( если уравнение имеет 2 корня, то в ответ запишите сумму корней уравнения): lg (4x – 3) = 2lgx.
Ответ:1010 IV метод.
5) Решите уравнение 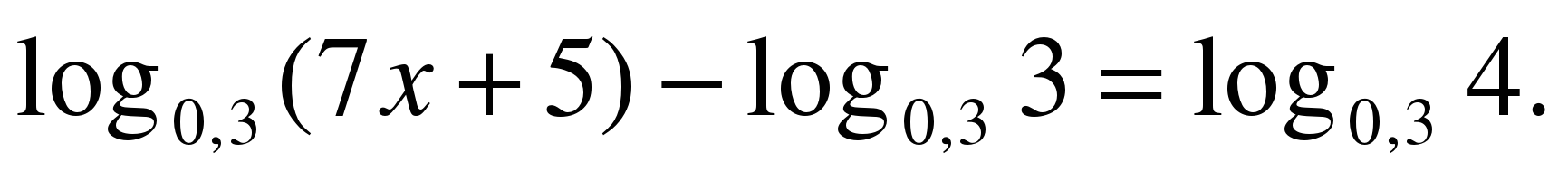
Ответ: х=1; I метод.
Укажите наименьший корень уравнение 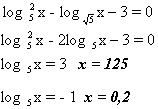
Ответ: х=0,2, III метод.
IV. Работа по группам (на карточках – задания разного уровня).
Учащиеся обсуждают решение уравнений в группах, определяют методы решения каждого уравнения, составляют план решения. Учащиеся, которые выбрали I уровень, решают уравнения самостоятельно (с последующей проверкой ответов), учащиеся II и III уровня решают уравнения на доске (по одному ученику от каждой группы).
Задания на карточках: I уровень (2 балл).
1. Решите уравнение 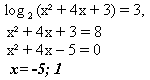
Ответ:х=1;х=-5 (I метод).
2. Решите уравнение log4(10-х)+ log4(х-3)=-1
Ответ: х = 4; х=9(IV метод).
3. Сколько различных корней имеет уравнение 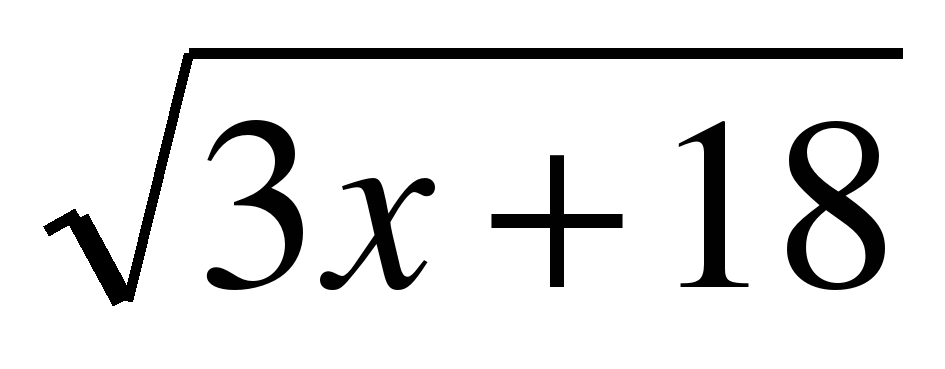 log4(x+4)=0
log4(x+4)=0
Ответ:1. (х1 = –3; II метод).
II уровень (3 балла).
1. Решите уравнение 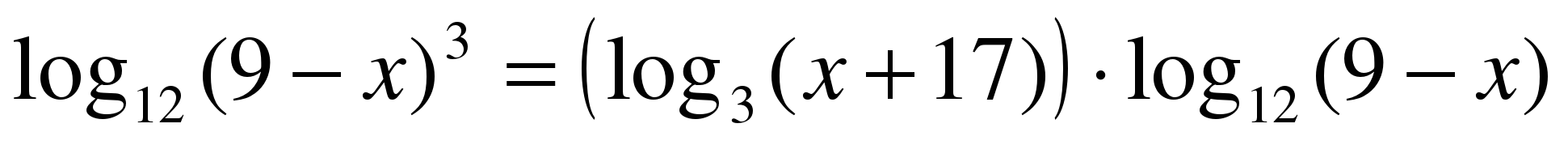 . Если уравнение имеет более одного корня, то в ответе укажите их сумму.
. Если уравнение имеет более одного корня, то в ответе укажите их сумму.
2. Найдите наибольший корень уравнения 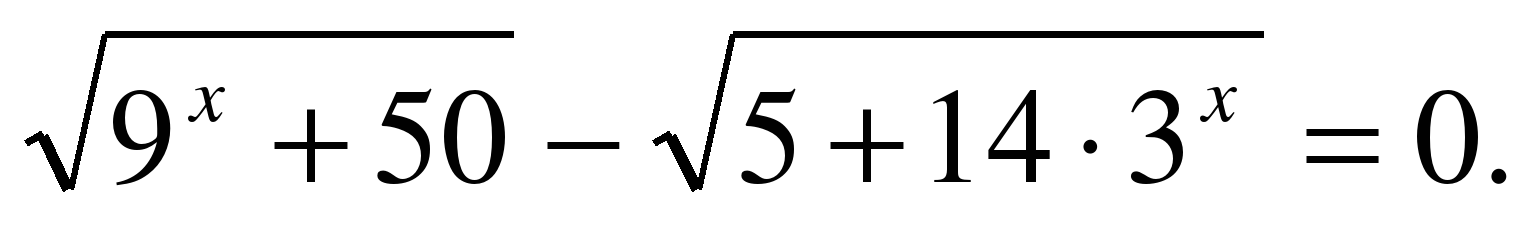
3. Решите уравнение 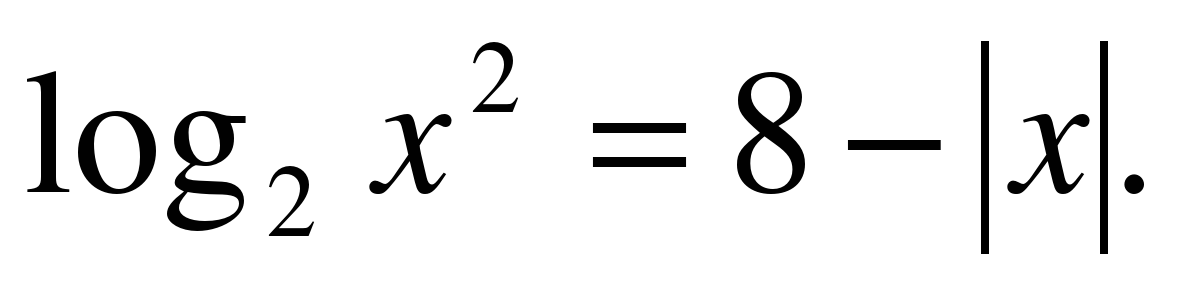 Если уравнение имеет больше одного корня, то в ответе укажите произведение его корней.
Если уравнение имеет больше одного корня, то в ответе укажите произведение его корней.
III уровень (4 балла)
С1. Решите уравнение lg (x+ 7) – lg (x+ 5) = 1.
С2. Решите уравнение 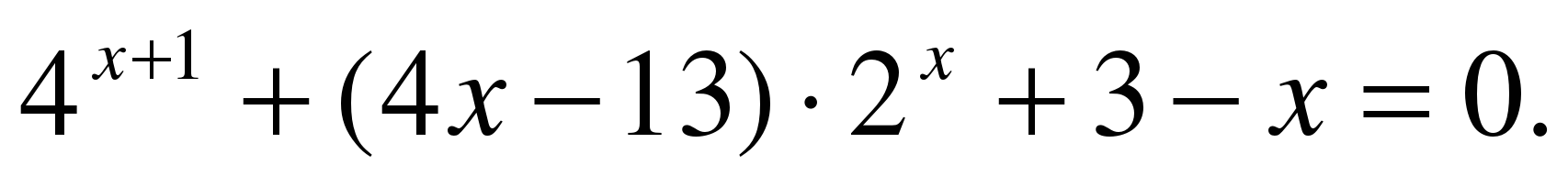
С3 Решите уравнение 4log64(х-3)+log 25 =50
Учащиеся проверяют решение уравнений и выставляют баллы за верные ответы. Самопроверка, самоконтроль.
Решение уравнений.
II уровень.
1. Решите уравнение 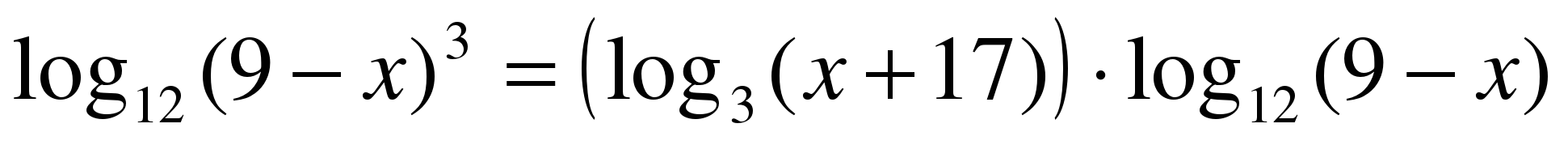 . Если уравнение имеет
. Если уравнение имеет
более одного корня, то в ответе укажите их сумму.
Решение. 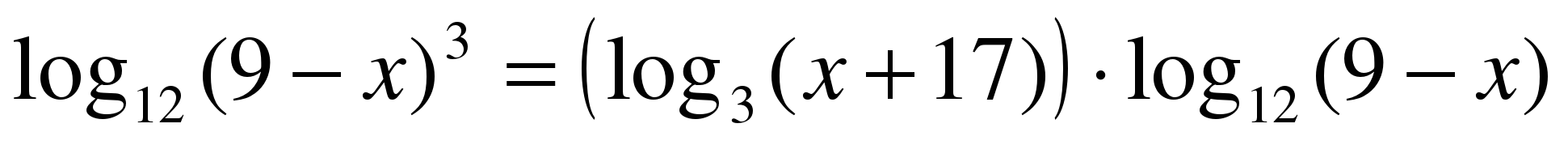 ,
, 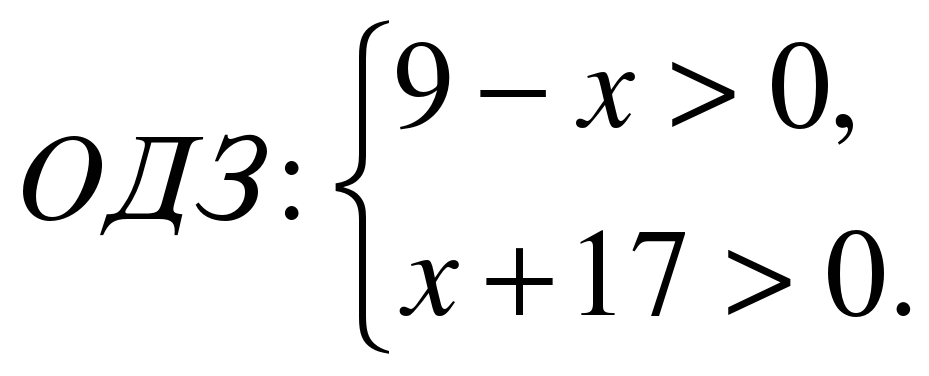
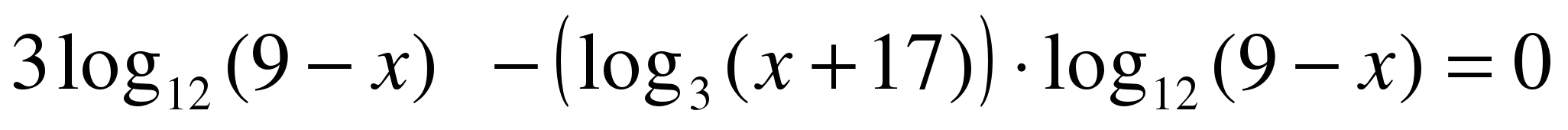 ,
, 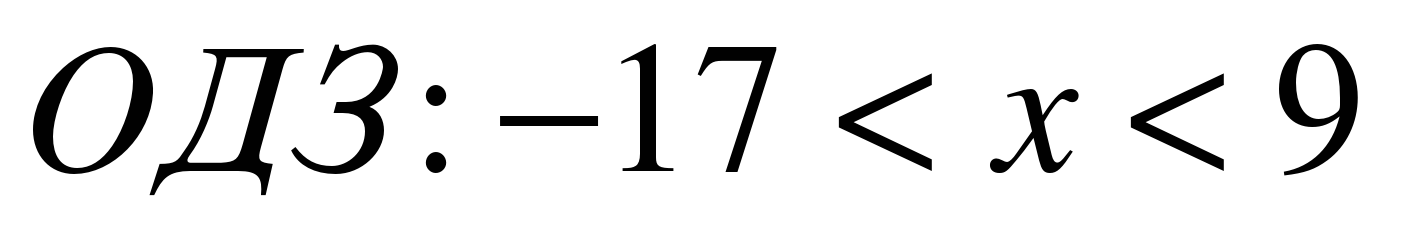 .
.
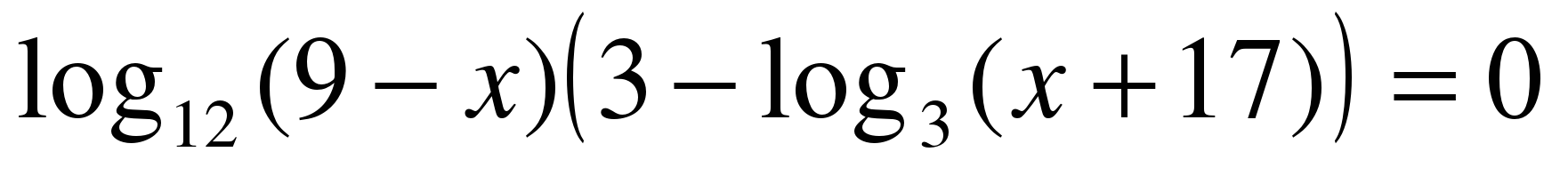 ,
,
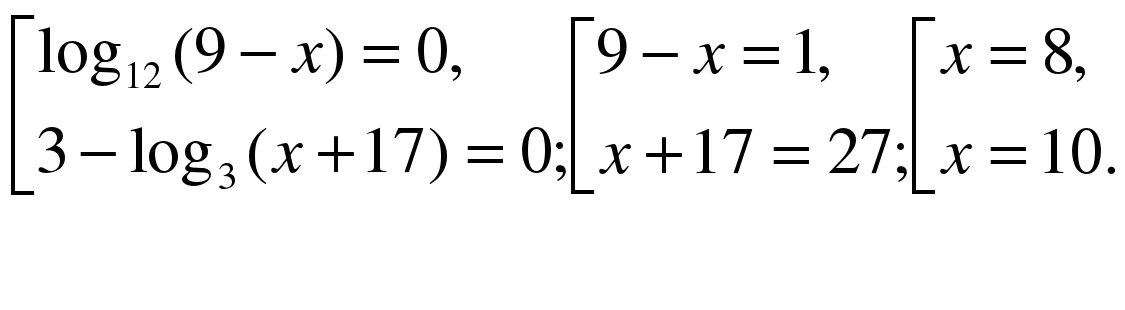
В ОДЗ входит корень х = 8. Ответ. 8.
2. Найдите наибольший корень уравнения 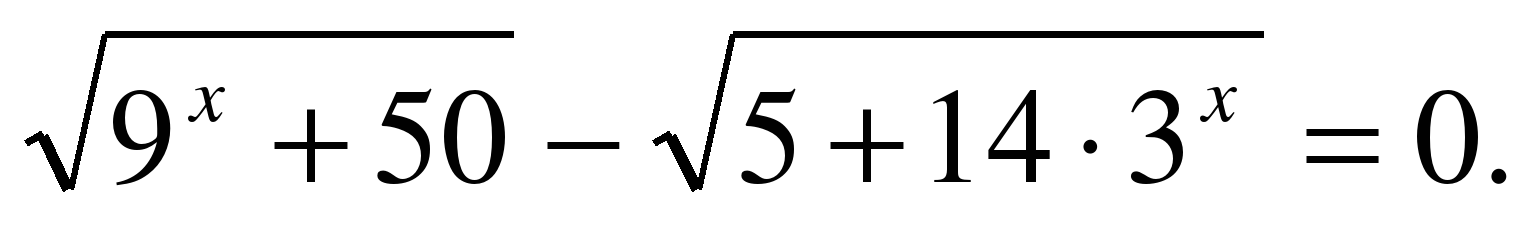
Решение. 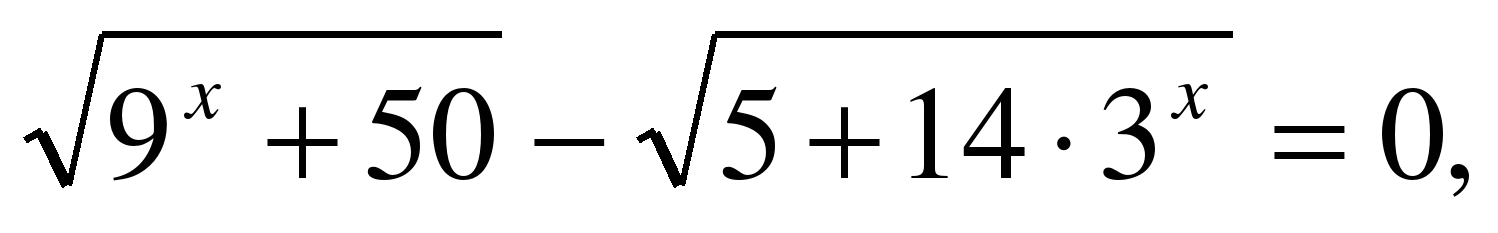 ОДЗ: х – любое действительное число,
ОДЗ: х – любое действительное число,
т.к. функция монотонная, то
Введем новую переменную
тогда
– наибольший корень. Ответ. 2.
3. Решите уравнение 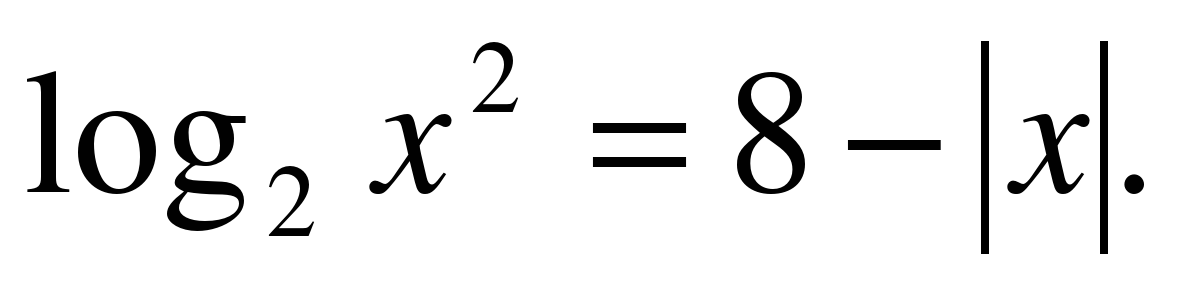 Если уравнение имеет более одного корня,то в ответе укажите произведение его корней.
Если уравнение имеет более одного корня,то в ответе укажите произведение его корней.
Решение.
1случай. При x0 функция возрастает, а функция убывает. Значит, уравнение , если имеет корень, то он
единственный. Находим его подбором: х=4.
2 случай. При x0 функция убывает, а функция
возрастает. Значит, уравнение , если имеет корень, то он единственный. Находим его подбором: х = – 4;
Ответ. – 16.
III уровень.
2. Решите уравнение 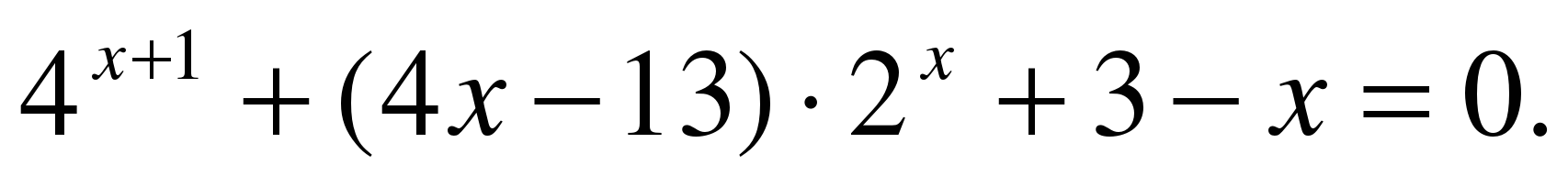
Решение. 1) Введем новую переменную
Получаем квадратное уравнение, в котором переменную х будем
считать параметром:
2) на R,
значит, уравнение имеет не более одного корня. Находим его подбором: х=1.
Ответ. 1; – 2.
V. Тестирование (задания 1 части оцениваются в 1 балл, задания 2 части – 1-2 балла).
ЧАСТЬ 1
1. Найдите сумму корней уравнения
2. Решите уравнение
3. Решите уравнение
4. Решите уравнение
Если уравнение имеет более одного
корня, то в ответе укажите их сумму.
5. Найдите количество корней уравнения
Если уравнение имеет более одного
корня, то в ответе укажите их сумму.
ЧАСТЬ 2
6.Решите уравнение
Если уравнение имеет более одного корня, то в ответе укажите их сумму.
7. Найдите сумму всех корней уравнения
8.Решите уравнение
Если уравнение имеет более одного корня, то в ответе укажите их сумму.
9. Решите уравнение
Ответы на слайдах.
Самопроверка по ответам. Выставление баллов в рейтинговый лист.
(Оценка за тест: "3" – 5-6 б., "4" – 7-8 б., "5" – 9б.)
VI. Подведение итогов
Учащиеся подсчитывают итоговые баллы по теме, переводят в оценку.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект урока по математике "Решение логарифмических уравнений" (0.2 MB)
Конспект урока по математике "Решение логарифмических уравнений" (0.2 MB)
 0
0 891
891 129
129 Нравится
0
Нравится
0


