Цель урока: изучение алгоритма нахождения наибольшего общего знаменателя; формирование навыков нахождения НОД чисел.
Развитие мыслительных операций; математической речи учащихся, познавательного интереса к предмету.
Воспитание коммуникативных навыков учащихся, аккуратности и сознательного отношения к учению.
Ход урока.
1. Орг. момент.
2. Мотивирование учеников к учебной деятельности.
Теоретический опрос: игра «Перестрелка»
1. Какие числа называются простыми числами?
2. Назови наименьшее простое число?
3. Является ли число 1 простым числом?
4. Сколько четных простых чисел?
5. Какое число называется составным числом?
6. Какие простые числа называются числами-близнецами?
7. Имеются ли простые числа, которые оканчиваются на 0?
8. Признак делимости на 3. Признак делимости на 9?
9. Можно ли назвать данное произведение-разложением на множители: а)3*4*5*7?
10. Можно ли назвать данное произведение-разложением на множители: а)2*3*5*7?

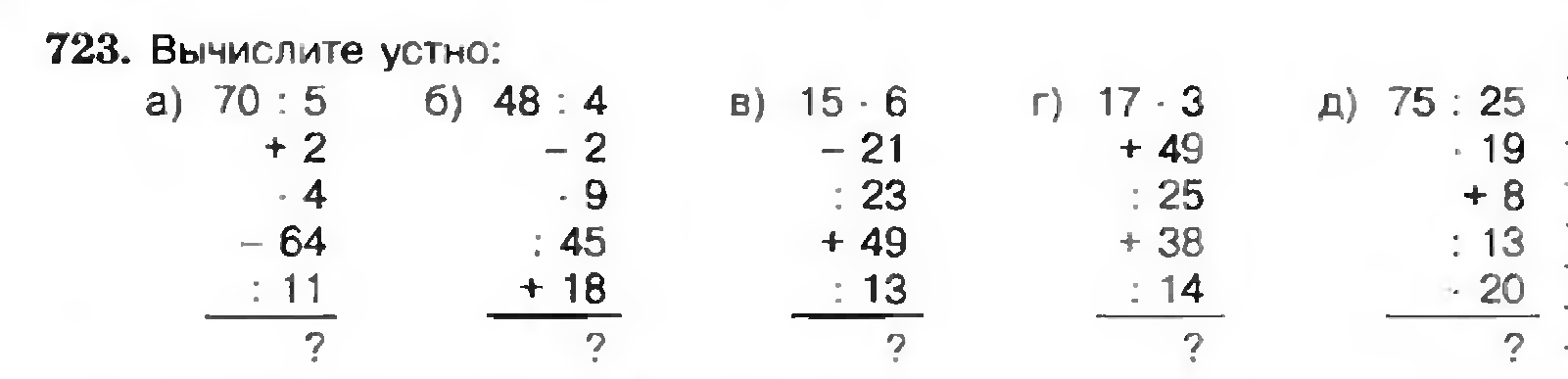
3. Устный счет. Игра «Кто быстрее» Угадать слово.
4. Изучение новой темы:
1) Учащиеся записывают в тетради число и тему урока.
И формулируют цель урока.
Задание: Учащиеся самостоятельно по учебнику ищут ответ на вопрос: «Какое число называют наибольшим общим делителем данных чисел»?
2) К доске вызывается ученик, который рассказывает нахождение НОД способом перебора, остальные ученики слушают и делают записи в тетрадях.
Стратегия «Смайлик»
3) Проблемный вопрос: Найти НОД(462 и 630)=?
Можно ли использовать метод перебора для нахождения НОД чисел?
4) Задание: Учащиеся самостоятельно изучают алгоритм нахождения НОД чисел способом разложения на простые множители.
Полную информацию смотрите в файле.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект урока по математике по теме "Наибольший общий делитель" (86.5 КB)
Конспект урока по математике по теме "Наибольший общий делитель" (86.5 КB)
 0
0 535
535 58
58 Нравится
0
Нравится
0


