Конспект урока по математике по теме «Касательная к графику функции. Обобщающий урок»

Цель: приведение усвоенных понятий в систему (предусматривающую раскрытие и усвоение связей и отношений между ее элементами).

Развивающие задачи: развитие логического мышления, грамотного математического языка, алгоритмической культуры.

Воспитательные задачи: формирование самостоятельности, аккуратности, точности, понимания значимости математики для общественного прогресса.

Оборудование урока:

1. Экран, проектор, ноутбук, презентация с иллюстративным материалом.

2. Учебник Алимова Ш. А. «Алгебра и начала анализа 10-11», М., Просвещение, 2005 г.

3. Листы с задачами из открытого банка заданий ЕГЭ по математике.

4. Листы с обязательными задачами (образец домашнего задания).

Ход урока:

1. Тема и цель урока.

Учитель сообщает тему, обосновывает цель (создание системы базовых знаний и умений – необходимое условие формирования творческой личности), тема и цель урока – на экране.

Вспомним определение касательной: касательная к кривой в точке Р определяется как предельное положение секущей при приближении точки по кривой к точке Р.

Слайд «Определение касательной».

2. Начальная мотивация учебной деятельности.

Учитель напоминает, зачем строили касательные к графикам малоизученных функций.

Учебник стр. 248, рис. 112

В окрестности нуля график синуса практически совпадает с прямой y = x, а линейная функция изучена вдоль и поперек.

Строя касательные к графикам функций с помощью аналитического метода, Г. Лейбниц одновременно с И. Ньютоном пришел к революционному открытию производной функции, cоздал математический аппарат, позволяющий рассчитывать динамические процессы, происходящие в реальности.

3. Актуализация опорных знаний.

Учитель: Как связано понятие производной функции с построением касательной к графику этой функции? (значение производной в точке касания равно тангенсу угла наклона касательной к оси абсцисс).

Слайд «Геометрический смысл производной»

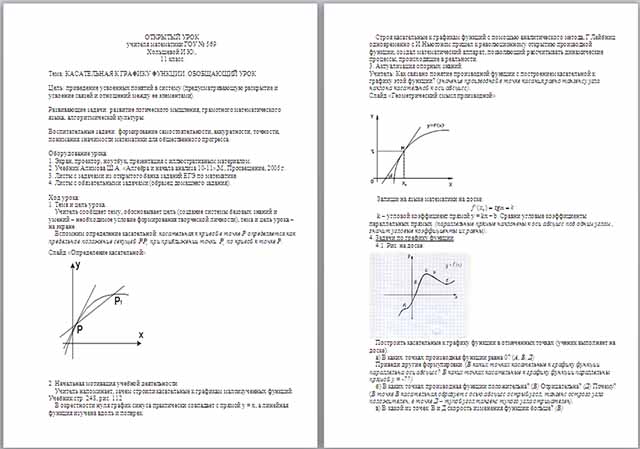
4. Задачи по графику функции.

4. 1. Рис. на доске:

Построить касательные к графику функции в отмеченных точках (ученик выполняет на доске).

а) В каких точках производная функции равна 0? (А, В, Д)

Приведи другие формулировки. (В каких точках касательные к графику функции параллельна оси абсцисс? В каких точках касательные к графику функции параллельны прямой у = -7?)

б) В каких точках производная функции положительна? (В) Отрицательна? (Д) Почему? (В точке В касательная образует с осью абсцисс острый угол, тангенс острого угла положителен, в точке Д – тупой угол тангенс тупого угла отрицателен).

в) В какой из точек В и Д скорость изменения функции больше? (В)

Почему? (Касательная круче, угловой коэффициент по модулю больше)

4. 2. Рис. на доске:

Объясните, как найти значение производной в точке касания.

Полную информацию смотрите в файле.