Конспект урока по математике на тему «Длина окружности, площадь круга, шар»

Цели урока:

1. Систематизировать, обобщить знания учащихся, проверить уровень освоения темы.

2. Прививать любовь к математике, желание познать новое, неизведанное, воспитывать честность в оценке своих знаний.

3. Развить творческое отношение к делу, самостоятельность.

План урока.

1. Теоретические вопросы.

2. Практическое задание.

3. Устный счет.

4. Игра «Светофор».

5. Музыкальная пауза.

6. Игра «Умеете ли вы считать?»

7. Зарядка.

8. Практическая работа «Определение неизвестных величин».

9. Из истории математики.

10. Математический диктант.

11. Подведение итогов урока. Задание на дом.

Ход урока.

I. Теоретические вопросы.

1. Каким свойством обладают точки окружности? [Точки окружности равноудалены от одной точки О]

2. Какой отрезок называется радиусом? Диаметром? [определения]

3. Чему равно отношение длины окружности к длине еѐ диаметра? [Отношение длины окружности к длине еѐ диаметра всегда одно и то же. Его обозначают буквой π, π ≈ 3 1/7]

4. Запишите формулу для вычисления длины окружности? [с = π d = 2 π r]

5. Что называют кругом? Приведите примеры. [Кругом называют часть плоскости, ограниченную окружностью. Например, дно стакана, поверхность крышки консервной банки]

6. Запишите формулу для вычисления площади круга? [S = π r ² ]

7. Приведите примеры тел, имеющих форму шара? [волейбольный мяч, глобус, арбуз]

II. Практическое задание.

Древнегреческий математик Архимед установил, что длина окружности  относится к длине диаметра приближенно как 22 : 7. Найдите длину окружности, диаметр которой 4,2 дм.

[Решение:  c/d = 22/7. с -  ?

с = π d, с = 22/7 * 4,2=(22 * 4,2)/(7/1) = (22 * 0,6)/1 = 132дм ]

III. Устный счет.

1. Вычислите длину окружности, диаметр которой равен: 1см; 1дм; 3дм; 10см; 0,1м.

2. Вычислите длину окружности, диаметр которого равен: 0,5 дм; 5 дм; 50см; 100мм; 0,05м.

3. Вычислите площадь круга, диаметр которого равен: 2см; 20см; 0,2см.

IV. Игра «Светофор».

Каждому ученику раздаются конверты, в которых содержатся: 3 круга (красный, желтый, зеленый); 5 квадратов; 1 треугольник – половина квадрата. Учитель готовит для игры 10 вопросов, на которые сам же отвечает. Ответ может быть не верным, неточным, верным. Ученики сигнализируют соответственно красным, желтым или зеленым кругом. Учитель включает действующую модель светофора, чтобы ученики могли видеть, верно ли они сигналили.

Если ученик верно оценил ответ, то зарабатывает треугольник, если даны два верных ответа, то квадрат. Ученик заработавший 4,5 и 5 квадратов получает оценку «5»; 4 квадрата – «4»; 3,5 квадрата – «3» и наконец, 3 квадрата – «2».

Вопросы:

1. Запишите формулу для вычисления длины окружности (через r)

2. Что называют кругом?

3. Дайте определение диаметра.

4. Запишите формулу для вычисления площади круга.

5. Запишите формулу для вычисления длины окружности (через d)

6. Что такое число π?

7. Что мы понимаем под числом π?

8. Какой отрезок называется радиусом?

9. Каким свойством обладают точки сферы?

10. Покажите на рисунке круг и окружность.

Весь материал - в документе.

Муниципальное образовательное учреждение Иркутского района муниципального образования

«Хомутовская средняя общеобразовательная школа №2»

Открытый урок по теме

«Длина окружности, площадь круга, шар»

7 класс

Игнатьева Валентина Александровна,

учитель математики

с.Хомутово, 2015

Форма проведения урока: игра «Поле чудес».

Цели урока:

1. Систематизировать, обобщить знания учащихся, проверить уровень освоения темы.

2. Прививать любовь к математике, желание познать новое, неизведанное, воспитывать честность в оценке своих знаний.

3. Развить творческое отношение к делу, самостоятельность.

Оборудование: магнитофон; проигрыватель; графопроектор; игра «Светофор»; таблица – игра «Сосчитай»; стенд, на котором помещены сочинения учащихся про шар.

План урока

1. Теоретические вопросы

2. Практическое задание

3. Устный счет

4. Игра «Светофор»

5. Музыкальная пауза

6. Игра «Умеете ли вы считать?»

7. Зарядка

8. Практическая работа «Определение неизвестных величин»

9. Из истории математики

10. Математический диктант

11. Подведение итогов урока. Задание на дом

Ход урока

I. Теоретические вопросы

1. Каким свойством обладают точки окружности? [Точки окружности равноудалены от одной точки О]

2. Какой отрезок называется радиусом? Диаметром? [определения]

3. Чему равно отношение длины окружности к длине еѐ диаметра? [Отношение длины окружности к длине еѐ диаметра всегда одно и то же. Его обозначают буквой π, π ≈ 3 1/7]

4. Запишите формулу для вычисления длины окружности? [с = π d = 2 π r]

5. Что называют кругом? Приведите примеры. [Кругом называют часть плоскости, ограниченную окружностью. Например, дно стакана, поверхность крышки консервной банки]

6. Запишите формулу для вычисления площади круга? [S = π r ² ]

7. Приведите примеры тел, имеющих форму шара? [волейбольный мяч, глобус, арбуз]

II. Практическое задание

Древнегреческий математик Архимед установил, что длина окружности относится к длине диаметра приближенно как 22 : 7. Найдите длину окружности, диаметр которой 4,2 дм.

[Решение: c/d = 22/7. с - ?

с = π d, с = 22/7 * 4,2=(22 * 4,2)/(7/1) = (22 * 0,6)/1 = 132дм ]

III. Устный счет

1. Вычислите длину окружности, диаметр которой равен: 1см; 1дм; 3дм; 10см; 0,1м.

1. Вычислите длину окружности, диаметр которого равен: 0,5 дм; 5 дм; 50см; 100мм; 0,05м.

1. Вычислите площадь круга, диаметр которого равен: 2см; 20см; 0,2см.

IV. Игра «Светофор»

Каждому ученику раздаются конверты, в которых содержатся: 3 круга (красный, желтый, зеленый); 5 квадратов; 1 треугольник – половина квадрата. Учитель готовит для игры 10 вопросов, на которые сам же отвечает. Ответ может быть не верным, неточным, верным. Ученики сигнализируют соответственно красным, желтым или зеленым кругом. Учитель включает действующую модель светофора, чтобы ученики могли видеть, верно ли они сигналили. Если ученик верно оценил ответ, то зарабатывает треугольник, если даны два верных ответа, то квадрат. Ученик заработавший 4,5 и 5 квадратов получает оценку «5»; 4 квадрата – «4»; 3,5 квадрата – «3» и наконец, 3 квадрата – «2».

Вопросы:

1. Запишите формулу для вычисления длины окружности (через r)

2. Что называют кругом?

3. Дайте определение диаметра.

4. Запишите формулу для вычисления площади круга.

5. Запишите формулу для вычисления длины окружности (через d)

6. Что такое число π?

7. Что мы понимаем под числом π?

8. Какой отрезок называется радиусом?

9. Каким свойством обладают точки сферы?

10. Покажите на рисунке круг и окружность.

V. Музыкальная пауза

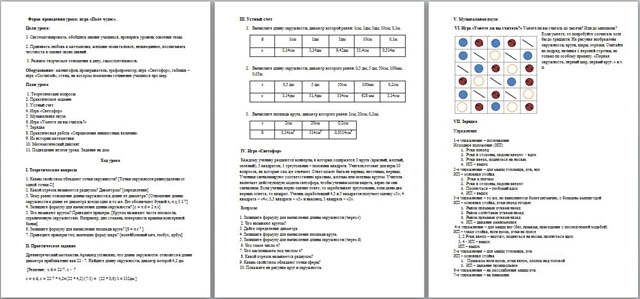
VI. Игра «Умеете ли вы считать?» Умеете ли вы считать до тысячи? Или до миллиона? Если умеете, то попробуйте сосчитать хотя бы до тридцати. На рисунке изображены окружности, круги, шары, отрезки. Считайте их подряд, начиная с верхней строчки, но только по особому правилу. «Первая окружность, первый шар, первый круг..» и т. д.

VII. Зарядка

Упражнения

1-е упражнение – потягивание

Исходное положение (ИП)

1. Руки вперед

2. Руки в стороны, ладони кверху - вдох

3. Руки вверх, подняться на носках

4. ИП – выдох

2-е упражнение – для мышц туловища, рук, ног

ИП – основная стойка

1. Руки к плечам

2. Руки в стороны, ладони кверху

3. Прогнуться – глубокий вдох

4. ИП – выдох

3-е упражнение – то же, но выполняется более ритмично, с большем амплитудой

ИП – основная стойка, руки перед грудью

1. Рывок прямыми руками назад

2. Рывок согнутыми руками назад

3. Рывок прямыми руками назад

4. ИП – дыхание равномерное

4-е упражнение – для мышц ног (бег, прыжки, приседание с последующей ходьбой)

ИП – узкая стойка, ноги врозь, руки на поясе

1, 2 Руки вверх – наружу, подняться на носки, прогнуться вдох

3, 4 - ИП – выдох

ИП – выдох

5-е упражнение – для мышц туловища, рук

ИП – основная стойка

1. Прыжком ноги врозь, руки вверх, хлопок над головой

2. ИП – дыхание произвольное

6-е упражнение – на расслабление мышц рук

7-е упражнение – на внимание

VIII. Практическая работа

1. r – 11мм1,1см; r -?

2. D = 22 мм = 2,2 см; d - ?

3. c = с = πd = 3,14 * 2,2 = 69,08мм = 6,908см ≈ 6,9 см; с - ?

4. S = π r ² = 3,14 * 11 ² = 3,14 * 121 = 379,94мм ² =3,7994 см ² ≈ 3,8 см ², S -?

IX. Из истории математики

Вопросы:

1. Кто, по приданию, из великих геометров древности сказал солдату, пришедшему его убить: «Не тронь моих кругов?» [Архимед]

2. Что, по приданию, завещал Архимед высечь на своем надгробном камне?

[Шар, вписанный в цилиндр]

1. Назовите великого геометра и механика Древней греции, нашедшего значение π ≈ 3 1/7. [В одном из наиболее известныхроизведений Архимеда изложены доказательсьва трех предложений, одно из которых следующее: отношение любой окружности к ее диаметру меньше 3 1/7 и больше 3 10/71. Иначе говоря, архимед указал границы числа π: 3 10/71

Познакомимся с происхождением некоторых терминов и понятий.

1. Циркуль – от лат. circulus – «круг»

2. Центр - от лат. «кентрон» - колющее оружие, которым в древности подгоняли животных в упряжке, а также острие ножки циркуля.

3. Радиус - от лат. radius – луч, спица в колесе

4. Диаметр - от греч. «диаметрос» - поперечник, насквозь измеряющий

5. Хорда – от греч. «корде» - струна, тетива

X. Математический диктант

Вариант 1:

1. Округлите число π до целых и запишите результат. [π ~ 3,14 ~ 3]

2. Вычислите длину окружности, диаметр которой равен 100 м, число π округлите до сотых. [d = 100м, π = 3,14; c = πd = 314 ( м)].

3. Напишите формулу по которой можно вычислить площадь круга, если известна длина его радиуса. [S = πr ² ]

4. Вычислите площадь круга, радиус которого равен 2 дм, округлив число π до сотых. [ r = 2 дм, π = 3,14; S = πr ² = 3,14 * 22 = 12,56 (дм ² )]

5. Начертите окружность. Обозначьте буквой М еѐ центр. Проведите в этой окружности радиус МВ и диаметр КД.

Вариант 2:

1. Округлите число π до десятых и запишите результат. [π ~ 3,14 ~ 3,1]

2. Вычислите длину окружности, радиус которой равен 5 дм, число π округлите до сотых. [r = 5 дм, π = 3,14; c = 2πr = 2 * 3,14 *5 = 31,4 ( дм)].

3. Напишите формулу по которой можно вычислить площадь круга, если известна длина его радиуса. [S = πr ² ]

4. Начертите окружность. Обозначьте буквой О еѐ центр. Проведите в этой окружности радиус ОВ и диаметр КМ.

5. Вычислите площадь круга, радиус которого равен 1 м, округлив число π до сотых. [ r = 1м, π = 3,14; S = πr ² = 3,14 * 12 = 3,14 (м ² )]

XI. Подведение итогов урока. Задание на дом.

Решите следующую задачу: Всем известны пушкинские строки:

У лукоморья дуб зеленый,

Золотая цепь на дубе том.

И днем и ночью кот ученый

Все ходит по цепи кругом.

Какую линию описывает кот при своем движении?

1. На первый взгляд может показаться, что он при таком движении описывает окружность. Но это неверно. Ведь цепь все время наматывается или сматывается с дуба так, что она натянута и образует касательные к окружности ствола. Ее концы при этом описывают линию, которая называется эвольвентой окружности, а окружность при этом называется эволютой данной эвольвенты.

2. Замкнутая цепь набросана на дуб так, что ученый кот при хождении по цепи описывает окружность, т. е. геометрическую фигуру. При этом он может ходить и налево и направо.

3. Цепь незамкнутая, но набросана на дуб так, что обвивает его спиралью сверху вниз. Спираль – геометрическая фигура. И в этом случае при хождении по цепи ученый кот идет то налево, то направо, как об этом говорит Пушкин.