РОССИЙСКАЯ ФЕДЕРАЦИЯ
Республика Саха (Якутия)
Муниципальное бюджетное образовательное учреждение
«Средняя общеобразовательная школа № 1»
Городского округа «Жатай»
_________________________________________________________________
677902 РС(Я), п. Жатай, ул. Северная, 50, тел. 42-64-38, факс 42-65-36
Иванова Любовь Ивановна
учитель математики
МБОУ СОШ № 1 ГО»Жатай»
Республика Саха (Якутия)
Урок математики 5 класс
Автор учебника Н. Я. Виленкин и др.
Тема: «Действия с десятичными дробями»
Итоговый урок
Урок строится на принципах системно – деятельностного обучения, включая практическую работу, работу в группах и парах, самостоятельную работу с использованием различных форм проверки.
Предполагаемые результаты:
Формулировать правила действия с десятичными дробями.
Выполнять вычисления с десятичными дробями.
Умение анализировать и осмысливать текст задачи.
Извлекать из текста необходимую информацию.
Осуществлять самоконтроль, проверяя ответ задачи на соответствие условию.
Строить логическую цепочку, оценивать полученный результат.
Исследовать простейшие числовые закономерности.
Развитие логического и критического мышления.
Цели урока:
Систематизировать, обобщить,повторить сложение, вычитание и умножение десятичных дробей.
Закрепить умение и навыки учащихся при решении упражнений и задач.
Развивать память, внимание, познавательные способности; воспитывать умение внимательно выслушивать мнение других, уважительно относиться ответам одноклассников; учить работать в группах; совершенствовать сочетание индивидуальной и коллективной форм работы учащихся.
Оборудование:
Магнитная доска.
Различные виды карточек.
Проектор и мультимедийное сопровождение.
Организационный момент.
Мотивация к учебной деятельности.
Решение задач - практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано, научиться ему можно. «Если вы хотите плавать, смело входите в воду, а если хотите решать задачи, то решайте их», - советовал учащимся известный американский математик Джорж Пойа в книге «Как решить задачу». Решение любой достаточно трудной задачи требует напряженного труда, воспитывает волю, упорство, развивает любознательность, смекалку. Это очень нужные качества в жизни человека, ведь даже в пословице говорится: «Ум без догадки гроша не стоит». Сегодня у нас урок по теме « Действия с десятичными дробями».
Устная работа «Думай и соображай»
Известно, какое важное значение имеет запятая в русском языке. От неправильной расстановки запятых смысл предложения может резко измениться. Например, « Казнить, нельзя помиловать» и «Казнить нельзя, помиловать». В математике от положения запятой зависит верность или неверность равенства.
Расставьте в следующих забавных равенствах запятые:
3,2 + 1,8 = 5; 63 - 2,7 = 60,3;
7,36 - 3,36 = 4; 3 - 1,08 = 4,08;
1,4 · 5 = 7; 1,2 · 50 = 60;
Даны две суммы :
7,82 + 5,64 + 3,47 + 1,23 и 1,18 + 3,36 + 5,53 + 7,77
Найдите сумму этих сумм.
Найдите сумму 20 чисел:
0,1 + 0,2 + 0,3 + … + 1,8 + 1,9 + 2.
4. В двух корзинах было поровну яблок. Если в одной корзины взять 8,2 кг яблок, то во второй окажется яблок в два раза больше, чем в первой. Сколько килограммов яблок было в каждой корзине?
5. Разрежьте фигуру на две равные части, оставляя клетки целыми. Какую часть фигуры составляет каждая полученная часть?
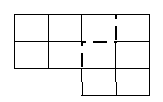
6. Найдите значение выражения:
( 0,5 –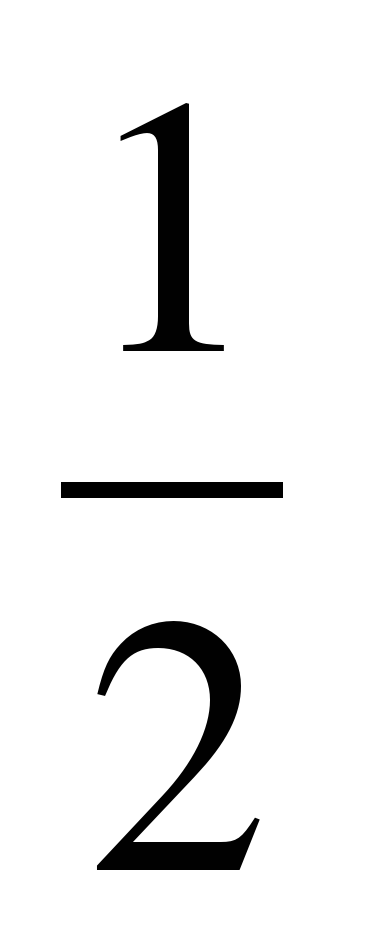 
) (13 – 2,46 · 3,54 ).
7. Вычислите наиболее простым способом:
а) 5,94 · 0,07 + 0,33 · 5,94 + 0,4 · 0,06
б) 6,85 ·3,2 – 6,85 · 1,7 + 1,5 · 4,15
III Дидактическая игра «Заполни таблицу»
| А | В | С | А + В + С | А + В | А + С | В + С |
|
0,8 |
1,3 |
2,7 |
|
|
|
|
|
|
7,3 |
15,5 |
|
|
18,3 |
|
|
|
0,7 |
|
15 |
|
|
12,2 |
|
|
|
|
26,7 |
22,4 |
23,5 |
|
|
|
|
|
|
20,6 |
12,9 |
18,5 |
В первой строке таблицы даны три числа А, В и С. Устно вычислите их общую сумму и парные суммы. Ответы запишите в соответствующие пустые клетки строки.
Во второй строке даны два числа и одна сумма. Заполните остальные пустые клетки строки.
В + С = 7,3 +15,5 = 22,8
А = 18,3 – 15,5 = 2,8
А + В = 2,8 + 7,3 = 10,1
А + В + С = 18,3 + 7,3 = 7,5
3 . В третьей строке дано одно число и две суммы.
1) А = 15 – 12,2 = 2,8
2) С = 12,2 – 4,7 = 7,5
3) А + +С = 2,8 + 7,5 = 10,3
4) А + В = 2,8 + 4,7 = 7,5
4 . Задача ( по четвертой строке). Три неразлучных друга – Вини – Пух Кролик и Пятачок – решили узнать свой вес. Но шкала весов до 20 килограммов была повреждена и показания по ней прочитать не представлялось возможным. Поэтому Вини – Пух взвесился сначала с Кроликом : получилось 22,4 кг; затем с Пятачком, получилось 23,5 кг; а затем они взвесились все вместе и получили 26,7 кг. Какова масса каждого из них в отдельности?
1) 26,7 – 22,4 = 4,3 (кг) – Пятачок;
2) 26,7 – 23, 5 = 3,2 (кг) – Кролик;
3) 22,4 – 3,2 = 19,2 (кг) – Вини – Пух.
5. Решили Вини - Пух, Кролик и Пятачок купить горшочек меда стоимостью 24 р. У Винни – Пуха с Кроликом было 20,6р., у Вини – Пуха с Пятачком 12,9р., а у Кролика с Пятачком 18,5р. Купят ли они горшочек меда, если сложат свои деньги? Сколько денег имел каждый?
1) 20,6 +12,9 + 18,5 = 52 (р) – удвоенная сумма Вини – Пуха, Кролика и Пятачка.;
2) 52 : 2 = 26( р) – было у Вини –Пуха, Кролика и Пятачка вместе;
3) 26 – 20,6 = 5,4 (р) – у Пятачка;
4) 26 – 12,9 = 13,1 (р) – у Кролика;
5) 26 – 18,5 = 7,5 (р) – у Винни –Пуха.
IV Денежные единицы и десятичные дроби
Каждое государство имеет собственную денежную единицу. В Росси это 1 рубль, в США – 1 доллар. Используют и более мелкие единицы : 1 копейку (0,01 рубля), 1 цент (0,01 доллара). Людям часто приходится обменивать деньги одного государства на деньги другого. Сейчас за 1 доллар США наши банки дают 56,26 р. (показать мультимедийно). Сколько российских денег нужно заплатить за 10, 100, 1000 долларов? Сколько будет стоить компьютер в России, если в Америке он стоит 2000 долларов?
2000 · 56,26 = 112520
Продолжи ряд чисел
Посмотрите на числа в каждом ряду; догадайтесь по какому признаку они собраны вместе и запишите еще по три числа в каждый ряд.
0,2; 0,7; 1,2; ….. ;
1,1; 2,2; 4,4; …..;
1,3; 2,5; 5; 6,2; 12,4; ……
VI. Задачи на движение
1. Из двух пунктов, расстояние между которыми 50км, выехали одновременно на встречу друг другу два всадника. Скорость одного 10,6км/ч, а скорость другого 14,4км/ч. Вместе с первым всадником выбежала собака, скорость которой 18,2 км/ч. Встретив второго всадника, она повернула назад; добежав до первого всадника, она снова повернула назад и бегала так до тех пор, пока всадники не встретились. Сколько километров пробежала собака до встречи всадников?
Вопросы:
Как можно найти расстояние, которое пробежала собака?
( Умножить ее скорость на время бега.)
Как найти время бега собаки?
( Оно равно времени движения всадников до встречи.)
Как найти время движения всадников до встречи?
(Нужно расстояние, которое они проехали до встречи, разделить на скорость их сближения)
Решение 1). 10,6 + 14,4 = 25 (км/ч) – скорость сближения всадников;
2). 50 : 25 = 2 (ч) – время встречи;
3). 18,2 · 2 = 36,4 (км) – пробежит собака.
Ответ : 36,4 км.
По железной дороге равномерно движется поезд длиной 136,5 м. Параллельно ему по шоссе едет велосипедист со скоростью 2,5 м/с. В какой – то момент времени поезд догоняет велосипедиста и обгоняет его за 7с. С какой скоростью едет поезд?
Вопросы:
1 . Как найти скорость поезда?
(разделить расстояние, пройденное поездом за время движения)
Как найти путь, пройденный поездом за 7с ?
( за 7 с поезд проходит расстояние равное сумме пути, пройденного велосипедистом и длины поезда)
Решение. 1) 2,5 · 7 = 17,5 (м) – проехал велосипедист за время обгона;
2) 17,5 + 136,5 = 154 (м) – проехал поезд за 7с;
3) 154 : 7 = 22 (м/с) – скорость поезда.
Ответ : 22м/с.
3 . Поезд проходит мост длиной 450м за 45,5 с, а мимо светофора за 15,5с. Найдите длину поезда и его скорость?
Решение. За 45,5с поезд проходит расстояние, равное длине моста и длине поезда вместе, а за 15,5 с расстояние равное длине поезда. Следовательно, длину моста (450м0 он проходит за 30с, т.е. его скорость равна 450 : 30 = 15 (м/с). Свою длину поезд «протягивает» мимо светофора за 15,5с, со скоростью 15 м/с. Значит, его длина равна
15 · 15,5 = 232,5 (м).
VII . Рефлексия учебной деятельности и оценивание учащихся.
Какое значение имеют десятичные дроби в жизни?
Перед Вами на доске расположены три ромашки разного цвета : белый, синий, желтый. Если Вам понравился урок, возьмите себе на память белый лепесток; если Вам не понравился урок – синий; если Вам все равно – желтый (учителю обратить внимание детей каких лепестков осталось меньше.)
Значение десятичных дробей в жизни велико. « С их помощью» строят дома, возводят мосты, лечат людей,измеряют время. В спортивных состязаниях решающую роль играют, порой, сотые доли секунды. Значение десятичных дробей трудно переоценить.
VIII.Домашнее задание (по карточкам).
Восстановите запись:
СУМК, А (7926,5
+ +
СУМК, А 7926,5
БАГАЖ 15853)
Решение.
Так как сумма дробей равна целому числу, то А = 5. Так А сумма – пятизначное число, а целые части – четырехзначные, то Б = 1, С = 7. У и К – цифры, большие 5, перебором находим решение.
Полный бидон с молоком весит 35кг.
Наполовину полный – 18,5кг.
Сколько весит бидон - ? кг
Решение.
Способ 1.
35 – 18,5 = 16,5 (кг) – половина молока.;
18,5 – 16,5 = 2(кг)– бидон.
Способ 2.
18,5 · 2 = 37 (кг) – все молоко и два таких бидона;
37 – 35 = 2 (кг) – бидон
Способ 3.
Х (кг) – половина молока.
Х + 18,5 =35,
Х = 16,5;
18,5 – 16,5 = 2 (кг) – бидон.
3, В пустые клетки квадрата вписать дроби так, чтобы по любой горизонтали, вертикали и диагонали сумма чисел была равна 3.
Получите свидетельство
Вход
Конспект урока по математике на тему: «Действия с десятичными дробями» (64.5 КB)
0
329
64
Нравится
0
