Геометрический смысл производной
Предварительная подготовка к уроку: учащиеся должны знать следующие темы: «производная степенной функции», «Правила дифференцирования», «Производные некоторых элементарных функций», «Геометрический смысл производной», уметь составлять уравнения касательной.
Цели урока:
1) образовательная: повторение определения углового коэффициента прямой, угла прямой и осью Ох; геометрического смысла производной, проверка знаний об уравнении касательной к графику функции;
2) воспитательная: воспитание познавательного интереса;
3) развивающая: развитие внимания и умения применять теоретические знания на практике.
Оборудование: записи на доске, проектор, тест.
Тип урока: урок-смотр знаний.
Ход урока
I. Организационный момент.
(Сообщение темы и целей урока).
II. Повторение.
Задание 1. Тест.
Задания этого типа предусматривают индивидуальную работу с последующей взаимопроверкой.
На слайдах отображаются задания с перечнем ответов для выбора, но на них не отмечаются правильные ответы, так как они будут представлены позже общим списком на отдельном слайде, чтобы ученики смогли самостоятельно осуществить взаимопроверку.
Слайд 1. - 1. Если k – угловой коэффициент касательной к графику функции y = 𝑓(x) в точке (х0; 𝑓(х0)) и α – угол между касательной и осью Ох, то геометрический смысл производной состоит в том, что:
а) k = 𝑓'(x);
б) k = 𝑓'(x0);
в) k = α;
г) tg α = 𝑓(x).
Слайд 2. - 2. Уравнение касательной к графику функции y = 𝑓(x) в точке (х0; 𝑓(х0)) имеет вид:
а) y = 𝑓'(x) + 𝑓'(x0)(x – x0);
б) y = 𝑓(x0) - 𝑓'(x)(x – x0);
в) y = 𝑓(x0) + 𝑓'(x0)(x – x0);
г) y = 𝑓'(x0)(x – x0) - 𝑓(x0).
Слайд 3. - 3. Угол между касательной к графику функции y = cos x в точке (0;1) и осью Ох равен:
а) 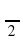 ;
;
б) 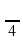 ;
;
в) 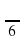 ;
;
г) 0.
Слайд 4. - 4. Если y = kx + b и k = tg α, то α – это угол:
а) между прямой y = kx + b и осью Ох;
б) между прямой y = kx + b и осью Оу;
в) между осями Ох и Оу;
г) между прямой y = kx + b и прямой y = kx.
Слайд 5. - 5. Угловой коэффициент касательной к графику функции 𝑓(х) = lnх в точке с абсциссой х0 = 2 равен:
а) 1;
б) 2;
в) 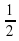 ;
;
г) 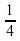 .
.
Слайд 6. - 6. Угол между прямой и осью Ох отсчитывается от положительного направления оси против часовой стрелки к прямой. Если угловой коэффициент касательной k х:
а) прямой;
б) развернутый;
в) острый;
г) тупой.
Слайд 7. - 7. Если графики функций у = k1x + b1 и y = k2x + b2 параллельны, то:
а) k1 = k2;
б) k1 k2;
в) b1 = b2;
г) k1 k2.
Слайд 8.
1. Б
2. В
3. Г
4. А
5. В
6. Г
7. А.
Задание 2. Запишите алгоритм нахождения уравнения касательной к графику функции y = 𝑓(x) в точке с абсциссой х0.
Алгоритм:
Текст указывается на слайде.
1) общий вид уравнения касательной: y = 𝑓(x0) + 𝑓'(x0)(x – x0);
2) найти 𝑓(x);
3) найти 𝑓'(x);
4) найти 𝑓'(x0);
5) подставить в уравнение касательной числовые значения 𝑓(x0), 𝑓'(x0), х0;
6) упростить полученное выражение.
- Проведем взаимопроверку. Проверяем тест.
- Оцените тест.
III. Практическая работа.
Задание 3. Составьте уравнение касательной к графику функции в точке с данной абсциссой х0.
(Выполняется самостоятельно по вариантам).
Вариант I
y = x – 5x2, x0 = 2.
Вариант II
y = ex, x0 =1.
Вариант III
𝑓(x) = cos x, x0 = 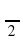 .
.
Все решения с ответами находятся на слайдах.
- Проверяем решение I варианта. Один ученик читает ответ;
Аналогичным способом проверяются ответы I и II вариантов.
Задание 4. Найдите абсциссы точек графика функции y = 2x3 + 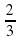 x +
x + 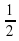 , в которой касательные, проведенные к нему, параллельны прямой у = 2х.
, в которой касательные, проведенные к нему, параллельны прямой у = 2х.
Данное задание выполняется у доски.
Решение этой задачи отображается на слайде.
Пусть k1 - угловой коэффициент касательных, k2 – угловой коэффициент прямой у = 2х. Так как касательные параллельны прямой, то k1 = k2.
k1 = 𝑓'(х) =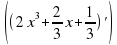 = 6х2 +
= 6х2 +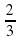 ; k2 = 2;
; k2 = 2;






 6х2 +
6х2 + 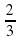 = 2 6х2
= 2 6х2 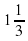 х2
х2 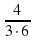 х2
х2 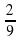 х1,2
х1,2
Ответ: 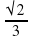 , -
, - 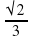 .
.
Задание 5. Найдите абсциссы точек графика функции у = 𝑓(х), в которых касательная к этому графику параллельна прямой у = рх.
а) 𝑓(х) = 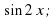 р = 2.
р = 2.
На слайде – Решение: Находим производную: 𝑓'(х) = (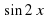 )' = 2
)' = 2 . Так как касательная параллельна прямой у = рх, то 2
. Так как касательная параллельна прямой у = рх, то 2 = р = 2. Отсюда
= р = 2. Отсюда  = 1, или 2х = 2πn, n ϵ Z.
= 1, или 2х = 2πn, n ϵ Z.
Ответ: х = πn, n ϵ Z.
б) 𝑓(х) =  3х+1; р =
3х+1; р =  .
.
На слайде – Решение: Находим производную: 𝑓'(х) = ( 3х+1)' =
3х+1)' =  . Так касательная параллельна прямой у = рх, то
. Так касательная параллельна прямой у = рх, то  = р =
= р =  .
.
Отсюда  3х+1 = 2, или х = 1.
3х+1 = 2, или х = 1.
Ответ: х =1.
в) 𝑓(х) = х +  ; р = 0.
; р = 0.
На слайде – Решение: Находим производную: 𝑓'(х) = (х +  )' = 1 +
)' = 1 +  . Так как касательная параллельной прямой у = 0, то 1 +
. Так как касательная параллельной прямой у = 0, то 1 +  = 0, или
= 0, или  = -1.
= -1.
Ответ: х = π + 2πn, n ϵ Z.
Задание 6. Выясните, при каких значениях а касательная, проведенная к графику функции у = х3 – ах в точке с абсциссой х0 = 1, проходит через точку М(2;3).
Задание выполняется у доски. См. слайд.
Задание 7. Прямая касается гиперболы у =  в точке (1;4). Найдите площадь треугольника, ограниченного этой касательной и осями координат.
в точке (1;4). Найдите площадь треугольника, ограниченного этой касательной и осями координат.
Дополнительное задание. См. слайд.
IV. Подведение итогов урока.
Учащиеся оценивают свои знания, умения по данной теме и работу на уроке.
Творческое домашнее задание.
Составь кроссворд по теме «Производная».
Приложение для работы на уроке
Все приложения отображаются на слайдах презентации и непосредственно используются по ходу работы учителя с заданиями.
Решения
Задание 3.
Вариант I.
Решение.
у = 𝑓(х0) + 𝑓'(х)(х – х0),
𝑓'(х) = (х – 5х2)' = 1 – 10х,
𝑓(х0) = 𝑓(2) = 2 – 5 22 = 2 – 20 = - 18,
22 = 2 – 20 = - 18,
𝑓'(х0) = 𝑓'(2) = 1 – 10  2 = - 19.
2 = - 19.
Итак, уравнение касательной у = - 18 – 19(х -2), у = 20 – 19х.
Ответ: у = 20 – 19х.
Вариант II.
Решение.
у = 𝑓(х0) + 𝑓'(х)(х – х0),
𝑓'(х) = (ех)' = ех,
𝑓(х0) = 𝑓(1) = е,
𝑓'(х0) = 𝑓'(1) = е.
Итак, уравнение касательной у = е + е(х – 1), или у = ех.
Ответ: у = ех.
Вариант III.
Решение.
у = 𝑓(х0) + 𝑓'(х)(х – х0),
𝑓'(х) = (сosx)' = - sin x,
𝑓(х0) = 𝑓( = 0,
= 0,
𝑓'(х0) = 𝑓'( = -1.
= -1.
Итак, уравнение касательной у = 0 – 1(х - 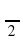 ), или у = - х +
), или у = - х + 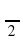 .
.
Ответ: у = - х + 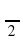 .
.
Задание 6.
Решение. Напишем уравнение касательной к графику функции 𝑓(х) = х3 – ах в точке с абсциссой х0 = 1. Общий вид касательной у = 𝑓(х0) + 𝑓'(х)(х – х0). Находим
𝑓(х0) + 𝑓(1) = 1 – а. Вычисляем производную 𝑓'(х) = (х3 – ах)' = 3х3 – а, а в точке х0 = 1 получим 𝑓'(1) = 3·12 – а = 3 – а. Итак, уравнение касательной имеет вид
у = 1 – а + (3 – а)(х – 1), или у = - 2 + (3 – а)х.
Так как касательная проходит через точку М(2;3), то верно равенство:
3 = - 2 + (3 – а) · 2, откуда 5 = 6 – 2а, т.е. а = 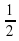 .
.
Ответ: а = 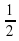 .
.
Задание 7.
Решение. Составим уравнение касательной. Для функции 𝑓(х) =  уравнение касательной в точке с абсциссой х0 = 1 имеет вид 𝑓(1) + 𝑓'(1)(х – 1).
уравнение касательной в точке с абсциссой х0 = 1 имеет вид 𝑓(1) + 𝑓'(1)(х – 1).
Вычисляем производную: 𝑓'(х) = ( -
-  .
.
Имеем 𝑓(1) = 4 и 𝑓'(1) = -4.
Значит, уравнение касательной имеет вид у = 4 – 4(х – 1), т.е. у = 8 – 4х.
Чтобы найти пересечение прямой с осями координат, надо в уравнение касательной подставить сначала х = 0, а потом у = 0. Получим, что касательная пересекается с осями координат в точках А(0;8) и В(2;0). Поэтому искомая площадь равна:
SAOB = 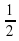 OB · OA =
OB · OA = 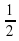 · 8 · 2 = 8 (кв. ед.).
· 8 · 2 = 8 (кв. ед.).
Ответ: S = 8 (кв. ед.).


 Получите свидетельство
Получите свидетельство Вход
Вход



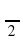 ;
; 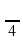 ;
;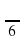 ;
;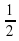 ;
;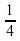 .
.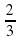 x +
x + 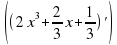 = 6х2 +
= 6х2 +

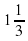 х2
х2 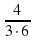 х2
х2 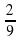 х1,2
х1,2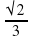 , -
, - 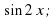 р = 2.
р = 2. 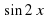 )' = 2
)' = 2








 Конспект урока по математике "Геометрический смысл производной" (31.4 КB)
Конспект урока по математике "Геометрический смысл производной" (31.4 КB)
 0
0 804
804 125
125 Нравится
0
Нравится
0


