Конспект урока по теме «Системы счисления. Непозиционные и позиционные системы счисления. Перевод целых и дробных чисел из n-ой в 10-ую систему счисления» для 10 (профильного) класса.
Цели урока:
Образовательная: рассмотреть историю систем счисления, деление на позиционные и непозиционные, дать понятие системы счисления, ее алфавита и основания, дать формулу развернутой записи числа, научить переводить целые и дробные числа из n-ой системы счисления в десятичную;
Воспитательная: способствовать воспитанию понимания значения чисел в истории человечества;
Развивающая: способствовать развитию кругозора, развитию аналитического мышления и навыков обработки информации.
Тип урока: Изучение новых знаний.
Формы и методы работы: Лекция, эвристическая беседа, программированный метод.
Материально-техническое обеспечение урока: компьютер, проектор, доска, презентация, выполненная в MS Power Point.
План урока:
Организация начала урока.
Изучение нового материала.
Закрепление знаний.
Подведение итогов урока.
Домашнее задание.
Ход урока.
Организация начала урока.
Организационный момент. Приветствие. Сообщение темы, цели и плана урока.
Изучение нового материала.
Мы с вами сегодня попытаемся раскрыть историю возникновения чисел и углубиться в мир систем счисления.
Давайте проанализируем запись числа с использованием арабских цифр, например, 111 и запись числа с использованием римских цифр, например III. «Чем отличается принцип получения значения многоразрядных чисел, записанных арабскими и римскими цифрами?»
Итак, и в том и в другом способе записи числа используют определенные цифры и имеются правила, которые позволяют понять значение числа по их записи, позволяют выполнять операции с числами.
Давайте запишем определение:
Система счисления – это способ представления чисел с помощью цифр и соответствующие правила действия над числами.
Однако в римском способе записи чисел значение цифры не зависит от ее позиции, а в арабском - зависит. Вспоминаем, что же такое непозиционная и позиционная системы счисления? В непозиционной системе счисления значение цифры не зависит от ее позиции. В позиционной системе счисления значение цифры зависит от ее позиции.
Самой распространенной из непозиционных систем счисления является римская. В качестве цифр используются буквы:
| I | V | X | L | С | D | M |
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
Значение цифры не зависит от ее положения в числе. Величина числа в римской системе счисления определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа – прибавляется.
В числе XXX цифра X встречается трижды и в каждом случае обозначает одну и ту же величину – 10. Так как величина используемой цифры одинакова, то получаем: XXX= 10+10+10=30.
В числе VII использованы цифры V,I,I. В данном случае меньшая цифра стоит справа от большей, поэтому мы прибавляем значение данных цифр и получаем: VII = 5+1+1=7.
В числе IV тоже использованы цифры V,I, но в данном случае меньшая цифра расположена слева от большей, поэтому мы вычитаем из большего значения меньшее и получаем: IV= 5-1=4.
В непозиционных системах счисления выполнять вычисления неудобно, потому что запись больших чисел требует введения новых символов, а также невозможно представлять дробные и отрицательные числа, сложно выполнять простейшие арифметические операции.
Первая позиционная система счисления была придумана еще в древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, так как в ней использовалось 60 цифр. При измерении времени мы до сих пор ее используем (основание равно 60 – в 1часе – 60 минут, в минуте – 60 секунд). Наиболее известна десятичная позиционная система счисления. В Индии впервые появилась знакомая всем нам сегодня десятичная система счисления.
Позиционных систем счисления существует бесконечное множество и отличаются они друг от друга алфавитом (упорядоченное множество цифр) и основанием (количество цифр в алфавите).
Давайте рассмотрим алфавиты различных позиционных систем счисления:
| Основание | Название | Алфавит |
| 10 | Десятичная | 0,1,2,3,4,5,6,7,8,9 |
| 2 | Двоичная | 0,1 |
| 8 | Восьмеричная | 0,1,2,3,4,5,6,7 |
| 16 | Шестнадцатеричная | 0,1,2,3,4,5,6,7,8,9,A(10),B(11),C(12),D(13),E(14),F(15) |
| 3 | … | … |
В системах счисления с основанием не больше 10 используют только арабские цифры, а если основание больше 10, то используют латинские буквы в алфавитном порядке (к примеру, шестнадцатеричная система счисления).
Для указания на основание системы, которой относится число, вводится индексное обозначение. Например, 2510 - это число указывает, что это десятичная система счисления. Обратите внимание, что нельзя говорить «двадцать пять», правильно произносить – «два пять».
В416 – шестнадцатеричное число. Индекс всегда записывается десятичным числом, так как в любой системе счисления ее основание будет равно 10 (один, ноль).
Давайте рассмотрим число 532. В нем самая первая цифра обозначает пять единиц, вторая – три десятка и третья – две сотни. Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим. Число 532 записано в свернутой форме. Для записи развернутой формы числа необходимо над каждым числом определить степень основания, в которую данное основание системы будет возводиться (начиная с нулевого), с самого крайнего целого числа. В развернутой форме запись числа в десятичной системе счисления будет выглядеть таким образом:
53210= 5*102 + 3*101 + 2*100, то есть позиция цифры показывает, в какую степень надо возвести основание в развернутой форме. Итак, мы с вами получили правило позиционной системы счисления: чтобы получить значение числа, надо цифры умножить на основание в степени позиции и сложить.
Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 532, 25 в развернутой форме будет записываться следующим образом:
532,2510 = 5*102 + 3*101 + 2*100 + 2*10-1 + 5*10-2.
В общем случае в десятичной системе счисления запись числа А10 , которое содержит n целых разрядов числа и m дробных числа, производится следующим образом: A10 = an-1*10n-1 + an-2*10n-2 + …+ a0*100 + a-1*10-1 + a-2*10-2 +…+ a-m*10-m. Запишите эту формулу в тетради.
Аналогично мы можем получить развёрнутую форму чисел в других системах счисления. Например, для двоичного числа. В двоичной системе счисления основание = 2, а ее алфавит состоит из двух цифр – 0 и 1. Следовательно, числа в двоичной системе в развернутой форме записываются в виде суммы разряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1. Рассмотрим пример двоичной системы счисления, в свернутой форме в двоичной системе выглядит таким образом:
A2 = 101,012.
В развернутой форме число в двоичной системе выглядит так:
A2 = 1*22 + 0*21 + 1*20 + 0*2-1 + 1*2-2 .
В общем случае в двоичной системе счисления запись числа A10 , которое содержит n целых разрядов числа и m дробных числа, производится следующим образом:
A2 = an-1 *2n-1 + an-2 *2n-2 +…+ a0 *20 + a-1 *2-1 + a-2 *2-2 +…+ a-m *2-m .
Так в восьмеричной системе основание равно 8, тогда записанное в свернутой форме восьмеричное число A8 = 673,28 в развёрнутой форме будет выглядеть так: A8 = 6*82 + 7*81 + 3*80 + 2*8-1.
Также в шестнадцатеричной системе счисления основание равно 16, тогда записанное в развернутой форме число A16 = 8A,F16 будет иметь вид:
A16 = 8*161 + A*160 + F*16-1.
Итак, в общем случае в системе счисления с произвольным основанием q запись числа Aq , которое содержит n целых разрядов числа и m дробных разрядов числа, производится следующим образом: Aq = an-1 *qn-1 + an-2 *qn-2 +…+ a0 *q0 + a-1 *q-1 + a-2 *q-2 +…+ a-m *q-m.
Чтобы перевести число, скажем, 12345N, из системы счисления с основанием 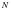 в десятичную систему, нужно умножить значение каждой цифры на
в десятичную систему, нужно умножить значение каждой цифры на 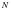 в степени, равной ее разряду:
в степени, равной ее разряду:
4 3 2 10 ← разряды
1 2 3 4 5N = 1·N4 + 2·N3 + 3·N2 + 4·N1 + 5·N0
Последняя цифра записи числа в системе счисления с основанием 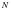 – это остаток от деления этого числа на
– это остаток от деления этого числа на 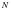 , две последние цифры – это остаток от деления на
, две последние цифры – это остаток от деления на 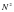 , и т.д.
, и т.д.
Какой остаток от деления на 8 числа 124? Какие две последние цифры от деления на 2 числа 1352?
У позиционной системы счисления может быть любое основание. Ребята, приведите свои примеры чисел в троичной, пятеричной и других системах счисления, запишите эти числа в развернутой форме.
Теперь, когда мы подробнее познакомились с позиционными системами счисления, давайте поговорим о переводе. Запишите подзаголовок: «Перевод чисел из n-ой системы счисления в 10-ую».
Возьмем произвольное двоичное число, например 11102. Запишем его в развернутой форме и произведем вычисления: 11102 = 1*23 + 1*22 + 1*21 + 0*20 = 1410.
Возьмем восьмеричное число 67,58. Запишем его развернутой форме и произведем вычисления: 6*81 + 7*80 + 5*8-1 = 55,62510.
Возьмем число 19F16 запишем в развернутой форме и произведем вычисления: 19F16 = 1*162 +9*161 +F*160 = 1*256 + 9*16 + 15*1= 41510.
Рассмотрим задачу из ЕГЭ.
Найдите основание системы счисления, в которой выполнено сложение: 144 + 24 = 201.
Для решения такого задания составляем уравнение: 144х + 24х = 201х. Запишем в развернутом виде: х2 + 4х + 4 + 2х + 4 = 2х2 + 1.
х2 – 6х – 7 = 0
D = 36 + 4 * 7 = 64.
Отрицательный корень не берем, т.к. он основание системы счисления положительно.
х = 7.
Закрепление знаний.
Теперь выполните перевод в десятичную систему счисления самостоятельно. Поочередно вызываются учащиеся для решения к доске, после чего всем классом проверяется и обсуждается решение.
11000010012;
1111110110,012;
457,38;
563,48;
AE3,616;
F18,C16 .
Задача: Найдите основание системы счисления, в которой выполнено умножение: 3·213 = 1043.
Подведение итогов урока.
Итак, сегодня мы узнали краткую историю систем счисления, а также вспомнили определения систем счисления, их алфавита и основания. Кроме того, мы изучили развернутую форму записи числа и научились переводу из n-ой в десятичную систему счисления.
Домашнее задание.
Выполните перевод в десятичную систему счисления:
11000000002;
11010111112;
1011001101,000112;
746,18;
174,28;
E26,A16;
B4B,716 .
Задачи из ЕГЭ:
В системе счисления с некоторым основанием десятичное число 83 записывается в виде 123. Укажите это основание.


 Получите свидетельство
Получите свидетельство Вход
Вход



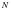 в десятичную систему, нужно умножить значение каждой цифры на
в десятичную систему, нужно умножить значение каждой цифры на 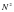 , и т.д.
, и т.д.








 Конспект урока по информатике «Системы счисления. Непозиционные и позиционные системы счисления. Перевод целых и дробных чисел из n-ой в 10-ую СС» (39.99 КB)
Конспект урока по информатике «Системы счисления. Непозиционные и позиционные системы счисления. Перевод целых и дробных чисел из n-ой в 10-ую СС» (39.99 КB)
 0
0 2025
2025 189
189 Нравится
0
Нравится
0


