Келтіру формулалары

19.02.13 жыл

Біліктілік: Оқушыларға сүйір бұрыштың тригонометриялық функциясының әрбір бұрышындағы синустыың, косинустың, тангенстің, котангенстің келтіру формулаларымен таныстыру, осы формулаларды тригонометриялық өрнектерді түрлендіруде және есептерді шығару кезінде қолдануды үйрету;

Дамытушылық: Оқушылардың ақыл-ойын дамыту, ойлау қабілетін жетілдіру.

Тәрбиелік: Оқушылардың алгебра пәніне қызығушылығын арттыру, оқушыларды алғырлыққа, шапшандыққа тәрбиелеу.

І. Ұйымдастыру.

ІІ. Үй тапсырмасын тексеру

ІІІ. Жаңа сабақ. “Ой қозғау”

ІҮ. Бекіту бөлімі.

1.Сәйкестендіру тесті

2.“Математикалық жәрмеңке” деңгейлік тапсырмалар

Ү. Бағалау

Егер бұрышының функциялары берілсе, онда оларды α бұрышына байланысты тригонометриялық функцияларға келтіру ыңғайлы.

Келтіру формулаларын k =1 ;2;3;4 болған жағдайда, өрнегін, яғни бұрыштары үшін қарастырамыз.

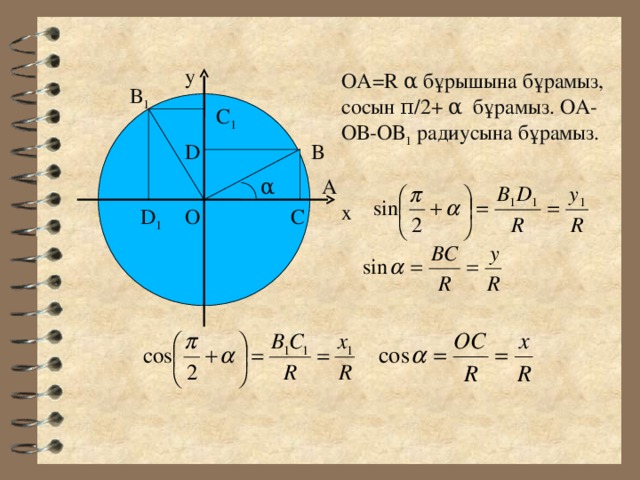
у

ОА= R α бұрышына бұрамыз, сосын π /2+ α бұрамыз. ОА- ОВ-ОВ 1 радиусына бұрамыз.

В 1

C 1

B

D

α

A

х

C

O

D 1

У

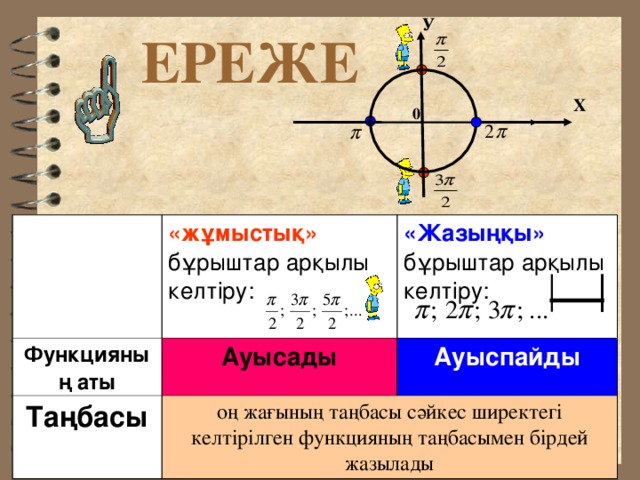
ЕРЕЖЕ

Х

0

Функцияның аты

«жұмыстық» бұрыштар арқылы келтіру:

«Жазыңқы» бұрыштар арқылы келтіру:

Ауысады

Таңбасы

Ауыспайды

оң жағының таңбасы сәйкес ширектегі келтірілген функцияның таңбасымен бірдей жазылады

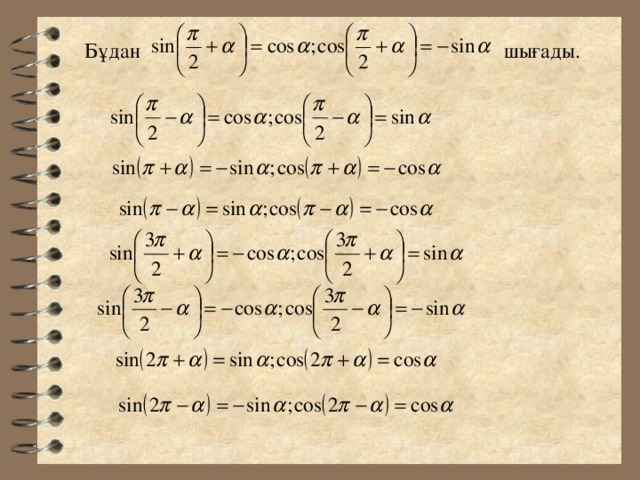
Бұдан шығады.

Жоғарыдағы формулаларды пайдаланып, tg α ,ctg α - н ің келтіру формуласын шығаруға болады.

Есте са қта!!!

• Егер келтірілген тригонометриялық функцияның аргументі (бұрышы) π ± α (180 ± α ), 2 π ± α (360 ± α ) түрінде болса, онда оның аты өзгермейді.
• Егер келтірілген тригонометриялық функцияның аргументі (бұрышы) π /2 ± α (90 ± α ), 3 π /2 ± α (270 ± α ) түрінде болса, онда синус косинусқа, косинус синусқа, тангенс котангенске, котангенс тангенске өзгереді;
• Келтіру формуласының оң жағының таңбасы сәйкес ширектегі келтірілген функцияныі таңбасымен бірдей жазылады.

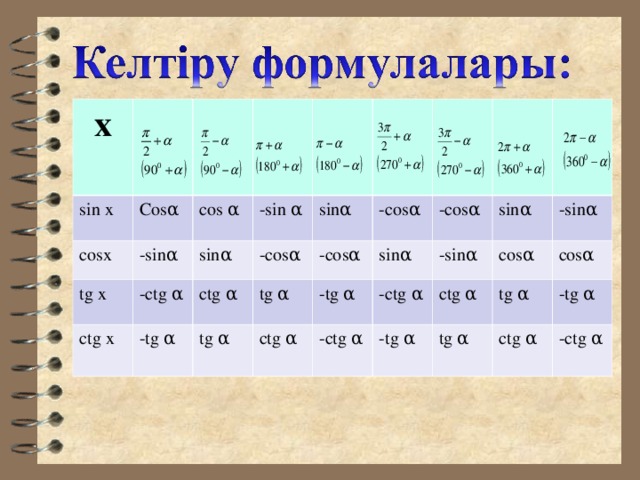
х

sin x

Cos α

cosx

cos α

-sin α

tg x

sin α

-ctg α

ctg x

-sin α

sin α

-cos α

ctg α

-tg α

tg α

tg α

-cos α

-cos α

ctg α

sin α

-tg α

-cos α

sin α

-sin α

-ctg α

-ctg α

-tg α

cos α

ctg α

-sin α

tg α

cos α

tg α

-tg α

ctg α

-ctg α

1. Сәйкестендіру тесті(өрнекті ықшамда)

tg( π - α )

cos α

ctg( π + α )

tg α

sin(360- α )

- tg α

cos(360- α )

ctg α

ctg(360- α )

- sin α

tg(360+ α )

- ctg α

Оқулықпен жұмыс №334

1. 2 .

а)75 ә) 150 б)200 бұрыштарының барлық тригонометриялық функциясын аргументі 45- тан аспайтын функциямен ауыстырыңдар.

1. 2 .