Календарно – тематическое планирование по МАТЕМАТИКЕ: АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА, ГЕОМЕТРИЯ
10 класс (углубленный уровень)
Учебник: 1) Г.К.Муравин, О.В.Муравина. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс. Углубленный уровень: учебник. М.: Дрофа. 2018г.
2) Е.В.Потоскуев, Л.И. Звавич. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10 класс. Углубленный уровень: учебник. М.: Дрофа. 2017г.
Е.В.Потоскуев, Л.И. Звавич. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10 класс. Углубленный уровень: задачник. М.: Дрофа. 2017г.
6 часов в неделю. По тематическому плану 204 часа.
| №урока
|
| № пунк та | Тема урока | Кол-во часов | Содержание | Дата проведения | Кор-ректи ровка | |||||||||||||||||
|
| План | факт |
| |||||||||||||||||||||
|
| 10а | 10б | 10а | 10б | ||||||||||||||||||||
|
|
|
| Повторение | 9 |
|
|
|
|
|
| ||||||||||||||
| 1 | Модуль «Алгебра и начала анализа» |
| Повторение. Числа и вычисления. Проценты | 1 | Решение задач с использованием свойств чисел и систем счисления, делимости, долей и частей, процентов, модулей чисел. Решение задач с использованием градусной меры угла. Модуль числа и его свойства. |
|
|
|
|
| ||||||||||||||
| 2 |
| Повторение. Многочлены. Дробно-рациональные выражения. Степени и корни | 1 | Решение задач с использованием свойств степеней и корней, многочленов, преобразований многочленов и дробно-рациональных выражений. |
|
|
|
|
| |||||||||||||||
| 3 |
| Повторение. Уравнения, системы уравнений | 1 | Решение задач на движение и совместную работу, смеси и сплавы с помощью линейных, квадратных и дробно-рациональных уравнений и их систем. |
|
|
|
|
| |||||||||||||||
| 4 |
| Повторение. Неравенства, системы неравенств
| 1 | Решение задач с помощью числовых неравенств и систем неравенств с одной переменной, с применением изображения числовых промежутков. Использование операций над множествами и высказываниями. Использование неравенств и систем неравенств с одной переменной, числовых промежутков, их объединений и пересечений. |
|
|
|
|
| |||||||||||||||
| 5 |
| Повторение. Функции, их свойства и графики. Арифметическая и геометрическая прогрессии | 1 | Решение задач с использованием числовых функций и их графиков. Использование свойств и графиков линейных и квадратичных функций, обратной пропорциональности и функции |
|
|
|
|
| |||||||||||||||
| 6 | Модуль «Геометрия» |
| Повторение. Фигуры на плоскости и их свойства. Измерения на плоскости | 1 | Решение задач с использованием свойств фигур на плоскости. Решение задач с использованием теорем о треугольниках, соотношений в прямоугольных треугольниках, фактов, связанных с четырехугольниками. Решение задач с использованием фактов, связанных с окружностями Решение задач на измерения на плоскости, вычисления длин и площадей. |
|
|
|
|
| ||||||||||||||
| 7 |
| Повторение. Векторы и координаты. Задачи на доказательства | 1 | Решение задач с помощью векторов и координат. Решение задач на доказательство и построение контрпримеров. Применение простейших логических правил. |
|
|
|
|
| |||||||||||||||
| 8,9 |
|
| Входная контрольная работа | 2 |
|
|
|
|
|
| ||||||||||||||
|
| Модуль «Алгебра и начала анализа» |
| Множества | 3 |
|
|
|
|
|
| ||||||||||||||
| 10 |
| Множества и операции над ними | 1 | Множества (числовые, геометрических фигур). Характеристическое свойство, элемент множества, пустое, конечное, бесконечное множество. Способы задания множеств. Подмножество. Отношения принадлежности, включения, равенства. Операции над множествами. Круги Эйлера. Конечные и бесконечные, счетные и несчетные множества. |
|
|
|
|
| |||||||||||||||
| 11 |
| Высказывания. Кванторы. Законы логики | 1 | Истинные и ложные высказывания, операции над высказываниями. Алгебра высказываний. Связь высказываний с множествами. Кванторы существования и всеобщности.Законы логики. Основные логические правила. Решение логических задач с использованием кругов Эйлера, основных логических правил. |
|
|
|
|
| |||||||||||||||
| 12 |
| Умозаключения. Теоремы | 1 | Умозаключения. Обоснования и доказательство в математике. Теоремы. Виды математических утверждений. Виды доказательств. Математическая индукция. Утверждения: обратное данному, противоположное, обратное противоположному данному. Признак и свойство, необходимые и достаточные условия. |
|
|
|
|
| |||||||||||||||
|
| Гл.1 | Функции и графики | 21 | Нули функции, промежутки знакопостоянства, монотонность. Наибольшее и наименьшее значение функции. Функции «дробная часть числа» |
|
|
|
|
| |||||||||||||||
| 13-16 |
| Понятие функции | 4 |
|
|
|
|
| ||||||||||||||||
| 17-21 |
| Прямая, гипербола, парабола и окружность | 5 |
|
|
|
|
| ||||||||||||||||
| 22-26 |
| Непрерывность и монотонность функций | 5 |
|
|
|
|
| ||||||||||||||||
| 27-32 |
| Квадратичная и дробно-линейная функции. Преобразование графиков | 6 |
|
|
|
|
| ||||||||||||||||
| 33 |
| Контрольная работа №1 на тему: «Функции и графики» | 1 |
|
|
|
|
| ||||||||||||||||
|
| Модуль «Геометрия» | Гл.1 | Введение в стереометрию | 5 | Наглядная стереометрия. Призма, параллелепипед, пирамида, тетраэдр. Основные понятия геометрии в пространстве. Аксиомы стереометрии и следствия из них. Понятие об аксиоматическом методе. . Построение сечений многогранников методом следов. Центральное проектирование. Построение сечений многогранников методом проекций. |
|
|
|
|
| ||||||||||||||
| 34 |
| Предмет стереометрии. Основные понятия. | 1 |
|
|
|
|
| ||||||||||||||||
| 35 |
| О некоторых пространственных фигурах | 1 |
|
|
|
|
| ||||||||||||||||
| 36 |
| Аксиомы стереометрии | 1 |
|
|
|
|
| ||||||||||||||||
| 37 |
| Следствия из аксиом. Способы задания плоскости | 1 |
|
|
|
|
| ||||||||||||||||
| 38 |
| Рисунки на доске и в тетради | 1 |
|
|
|
|
| ||||||||||||||||
|
| Гл.2 | Прямые в пространстве | 7 | Скрещивающиеся прямые в пространстве. Угол между ними. Методы нахождения расстояний между скрещивающимися прямыми.
|
|
|
|
|
| |||||||||||||||
| 39 |
| Классификация взаимного расположения двух прямых в пространстве | 1 |
|
|
|
|
| ||||||||||||||||
| 40 |
| Скрещивающиеся прямые | 1 |
|
|
|
|
| ||||||||||||||||
| 41,42 |
| Параллельные прямые в пространстве | 2 |
|
|
|
|
| ||||||||||||||||
| 43 |
| Угол между лучами в пространстве | 1 |
|
|
|
|
| ||||||||||||||||
| 44,45 |
| Угол между прямыми в пространстве. Перпендикулярные прямые | 2 |
|
|
|
|
| ||||||||||||||||
|
| Гл.3 | Прямая и плоскость в пространстве | 12 | Теоремы о параллельности прямых и плоскостей в пространстве. Параллельное проектирование и изображение фигур. Перпендикулярность прямой и плоскости. Ортогональное проектирование. Наклонные и проекции. Теорема о трех перпендикулярах.
|
|
|
|
|
| |||||||||||||||
| 46,47 |
| Параллельность прямой и плоскости | 2 |
|
|
|
|
| ||||||||||||||||
| 48,49 |
| Признак перпендикулярности прямой и плоскости. Построение перпендикулярных прямой и плоскости | 2 |
|
|
|
|
| ||||||||||||||||
| 50 |
| О прямых, перпендикулярных плоскости | 1 |
|
|
|
|
| ||||||||||||||||
| 51,52 |
| Перпендикуляр и наклонная к плоскости. Теорема о трех перпендикулярах | 2 |
|
|
|
|
| ||||||||||||||||
| 53,54 |
| Угол между прямой и плоскостью | 2 |
|
|
|
|
| ||||||||||||||||
| 55,56 |
| Параллельное проектирование и его свойства. Ортогональное проектирование | 2 |
|
|
|
|
| ||||||||||||||||
| 57 |
| Контрольная работа №2 «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости в пространстве» | 1 |
|
|
|
|
| ||||||||||||||||
|
|
| Гл.2 | Степени и корни | 14 | Степень с действительным показателем, свойства степени. Степенная функция и ее свойства и график. Четные и нечетные функции. Иррациональные уравнения. Взаимно обратные функции. Графики взаимно обратных функций.
|
|
|
|
|
| ||||||||||||||
| 58-60 |
| Степенная функция у=хn при натуральном n. | 3 |
|
|
|
|
| ||||||||||||||||
| 61-63 |
| Понятие корня n-ой степени. | 3 |
|
|
|
|
| ||||||||||||||||
| 64-66 |
| Свойства арифметических корней. | 3 |
|
|
|
|
| ||||||||||||||||
| 67-70 |
| Степень с рациональным показателем | 4 |
|
|
|
|
| ||||||||||||||||
| 71 |
| Контрольная работа №3 на тему: «Степени и корни» | 1 |
|
|
|
|
| ||||||||||||||||
|
| Гл.3 | Показательная и логарифмические функции | 18 |
|
|
|
|
|
| |||||||||||||||
| 72-77 |
| Функция y= aх | 6 | Простейшие показательные уравнения и неравенства. Показательная функция и ее свойства и график. Логарифм, свойства логарифма. Десятичный и натуральный логарифм. Преобразование логарифмических выражений. Логарифмические уравнения и неравенства. Логарифмическая функция и ее свойства и график. |
|
|
|
|
| |||||||||||||||
| 78-82 |
| Понятие логарифма | 5 |
|
|
|
|
| ||||||||||||||||
| 83-88 |
| Свойства логарифмов | 6 |
|
|
|
|
| ||||||||||||||||
| 89 |
| Контрольная работа №4 «Показательная и логарифмическая функции» | 1 |
|
|
|
|
| ||||||||||||||||
|
| Модуль «Геометрия» | Гл.4 | Плоскости в пространстве | 13 | Общий перпендикуляр двух скрещивающихся прямых. Углы в пространстве. Перпендикулярные плоскости. Площадь ортогональной проекции. |
|
|
|
|
| ||||||||||||||
| 90,91 |
| Параллельность плоскостей. Признаки параллельности плоскостей | 2 |
|
|
|
|
| ||||||||||||||||
| 92,93 |
| Свойства параллельных плоскостей | 2 |
|
|
|
|
| ||||||||||||||||
| 94 |
| Двугранный угол и его измерение | 1 |
|
|
|
|
| ||||||||||||||||
| 95,96 |
| Угол между двумя плоскостями | 2 |
|
|
|
|
| ||||||||||||||||
| 97,98 |
| Перпендикулярность плоскостей. Признаки перпендикулярности двух плоскостей | 2 |
|
|
|
|
| ||||||||||||||||
| 99 |
| Свойства перпендикулярных плоскостей | 1 |
|
|
|
|
| ||||||||||||||||
| 100 |
| Общий перпендикуляр двух скрещивающихся прямых | 1
|
|
|
|
|
| ||||||||||||||||
| 101 |
| Площадь ортогональной проекции многоугольника | 1 |
|
|
|
|
| ||||||||||||||||
|
|
| Гл.5 | Расстояния в пространстве | 5 | Расстояния между фигурами в пространстве. Геометрические места точек в пространстве. |
|
|
|
|
| ||||||||||||||
| 102, 103 |
| Расстояние от точки до фигуры | 2 |
|
|
|
|
| ||||||||||||||||
| 104 |
| Расстояние между фигурами | 1 |
|
|
|
|
| ||||||||||||||||
| 105, 106 |
| Геометрические места точек, связанные с расстояниями в пространстве | 2 |
|
|
|
|
| ||||||||||||||||
| 107 |
| Контрольная работа №5 «Плоскости в пространстве. Расстояния в пространстве» | 1 |
|
|
|
|
| ||||||||||||||||
|
| Модуль «Алгебра и начала анализа» | Гл.4 | Тригонометрические функции и их свойства | 57 |
|
|
|
|
|
| ||||||||||||||
| 108,109 | п.12 | Угол поворота | 2 | Радианная мера угла, тригонометрическая окружность. Тригонометрические функции чисел и углов. Формулы приведения, сложения тригонометрических функций, формулы двойного и половинного аргумента. Преобразование суммы, разности в произведение тригонометрических функций, и наоборот. Периодические функции и наименьший период. Тригонометрические функции числового аргумента Обратные тригонометрические функции, их главные значения, свойства и графики. Тригонометрические уравнения. Однородные тригонометрические уравнения. Решение простейших тригонометрических неравенств. Простейшие системы тригонометрических уравнений.
|
|
|
|
|
| |||||||||||||||
| 110-112 | п.13 | Радианная мера угла | 3 |
|
|
|
|
| ||||||||||||||||
| 113-115 | п.14 | Синус и косинус любого угла | 3 |
|
|
|
|
| ||||||||||||||||
| 116-118 | п.15 | Тангенс и котангенс любого угла | 3 |
|
|
|
|
| ||||||||||||||||
| 119-122 | п.16 | Простейшие тригонометрические уравнения | 4 |
|
|
|
|
| ||||||||||||||||
| 123-125 | п.17 | Формулы приведения | 3 |
|
|
|
|
| ||||||||||||||||
| 126-129 | п.18 | Свойства и график функции y= sin x | 4 |
|
|
|
|
| ||||||||||||||||
| 130-133 | п.19 | Свойства и график функции y= cos x | 4 |
|
|
|
|
| ||||||||||||||||
| 134-136 | п.20 | Свойства и график функции y= tgx и у=ctg x | 3 |
|
|
|
|
| ||||||||||||||||
| 137 |
| Контрольная работа №6 «Тригонометрические функции и их свойства» | 1 |
|
|
|
|
| ||||||||||||||||
| 138-141 | п.21 | Зависимости между тригонометрическими функциями одного и того же аргумента | 4 |
|
|
|
|
| ||||||||||||||||
| 142-145 | п.22 | Синус и косинус суммы и разности двух углов | 4 |
|
|
|
|
| ||||||||||||||||
| 146-148 | п.23 | Тангенс суммы и тангенс разности двух углов | 3 |
|
|
|
|
| ||||||||||||||||
| 149-152 | п.24 | Тригонометрические функции двойного угла | 4 |
|
|
|
|
| ||||||||||||||||
| 153-156 | п.25 | Преобразование произведения тригонометрических функций в сумму. Обратное преобразование | 4 |
|
|
|
|
| ||||||||||||||||
| 157-163 |
| Решение тригонометрических уравнений | 7 |
|
|
|
|
| ||||||||||||||||
| 164 |
| Контрольная работа №7 «Преобразование тригонометрических выражений. Решение тригонометрических уравнений» | 1 |
|
|
|
|
| ||||||||||||||||
|
|
| Гл.6 | Векторный метод в пространстве | 8 | Векторы и координаты. Сумма векторов, умножение вектора на число. Угол между векторами. Скалярное произведение. Уравнение плоскости. Формула расстояния между точками. Уравнение сферы. Формула расстояния от точки до плоскости. Способы задания прямой уравнениями. Решение задач и доказательство теорем с помощью векторов и методом координат. Элементы геометрии масс.
|
|
|
|
|
| ||||||||||||||
| 165 |
| Понятие вектора. | 1 |
|
|
|
|
| ||||||||||||||||
| 166 |
| Линейные операции над векторами | 1 |
|
|
|
|
| ||||||||||||||||
| 167 |
| Компланарные векторы | 1 |
|
|
|
|
| ||||||||||||||||
| 168 |
| Разложение вектора на плоскости | 1 |
|
|
|
|
| ||||||||||||||||
| 169 |
| Разложение вектора по трем некомпланарным векторам | 1 |
|
|
|
|
| ||||||||||||||||
| 170 |
| Определение и свойства скалярного произведения векторов | 1 |
|
|
|
|
| ||||||||||||||||
| 171 |
| Признак перпендикулярности двух векторов | 1 |
|
|
|
|
| ||||||||||||||||
| 172 |
| Применение векторного метода к решению стереометрических задач | 1 |
|
|
|
|
| ||||||||||||||||
|
| Гл.7 | Координатный метод в пространстве | 9 |
|
|
|
|
| ||||||||||||||||
| 173 |
| Координаты вектора в пространстве. Линейные операции над векторами в координатах | 1 |
|
|
|
|
| ||||||||||||||||
| 174 |
| Скалярное произведение векторов в координатах | 1 |
|
|
|
|
| ||||||||||||||||
| 175 |
| Проекции вектора на ось в координатах | 1 |
|
|
|
|
| ||||||||||||||||
| 176 |
| Декартовы прямоугольные координаты точки | 1 |
|
|
|
|
| ||||||||||||||||
| 177 |
| Решение простейших задач стереометрии в координатах | 1 |
|
|
|
|
| ||||||||||||||||
| 178 |
| Уравнение сферы. Уравнение плоскости | 1 |
|
|
|
|
| ||||||||||||||||
| 179 |
| Прямая в пространстве в координатах. Взаимное расположение прямой и плоскости в координатах | 1 |
|
|
|
|
| ||||||||||||||||
| 180 |
| Расстояние от точки до плоскости в координатах | 1 |
|
|
|
|
| ||||||||||||||||
| 181 |
| Контрольная работа №8 «Векторный и координатный методы в пространстве» | 1 |
|
|
|
|
| ||||||||||||||||
|
|
| Гл.5 | Элементы теории вероятностей и комбинаторики | 6 | Вычисление частот и вероятностей событий. Вычисление вероятностей в опытах с равновозможными элементарными исходами. Использование комбинаторики. Формула Бинома Ньютона. |
|
|
|
|
| ||||||||||||||
| 182-184 | п.27 | Понятие о вероятности | 3 |
|
|
|
|
| ||||||||||||||||
| 185-187 | п.28 | Вычисление числа вариантов | 3 |
|
|
|
|
| ||||||||||||||||
|
|
|
| Итоговое повторение | 17 |
|
|
|
|
|
| ||||||||||||||
| 188 |
|
| Повторение. Функции и графики. Область определения и область значений функции | 1 |
|
|
|
|
|
| ||||||||||||||
| 189 |
| Повторение. Непрерывность и монотонность функции | 1 |
|
|
|
|
|
| |||||||||||||||
| 190 |
|
| Повторение. Обратимость функции. Обратные тригонометрические функции | 1 |
|
|
|
|
|
| ||||||||||||||
| 191 |
| Повторение. Четность и нечетность функции. Периодичность функции. Преобразование графиков | 1 |
|
|
|
|
|
| |||||||||||||||
| 192 |
| Повторение. Уравнения и неравенства. Равносильные преобразования. Область допустимых значений | 1 |
|
|
|
|
|
| |||||||||||||||
| 193 |
| Повторение. Показательная функция. Показательные уравнения и неравенства | 1 |
|
|
|
|
|
| |||||||||||||||
| 194 |
| Повторение. Логарифмическая функция. Свойства логарифмов | 1 |
|
|
|
|
|
| |||||||||||||||
| 195 |
| Повторение. Логарифмические уравнения и неравенства | 1 |
|
|
|
|
|
| |||||||||||||||
| 196 |
| Повторение. Тригонометрические функции и их свойства | 1 |
|
|
|
|
|
| |||||||||||||||
| 197 |
| Повторение. Решение тригонометрических уравнений | 1 |
|
|
|
|
|
| |||||||||||||||
| 198 | Модуль «Геометрия» |
| Повторение. Аксиомы стереометрии и их следствия. | 1 |
|
|
|
|
|
| ||||||||||||||
| 199 |
| Повторение. Прямые в пространстве | 1 |
|
|
|
|
|
| |||||||||||||||
| 200 |
| Повторение. Прямая и плоскость в пространстве | 1 |
|
|
|
|
|
| |||||||||||||||
| 201 |
| Повторение. Плоскости в пространстве. Расстояния в пространстве | 1 |
|
|
|
|
|
| |||||||||||||||
| 202 |
| Повторение. Векторы и координаты в пространстве. | 1 |
|
|
|
|
|
| |||||||||||||||
| 203,204 |
|
| Итоговая контрольная работа | 2 |
|
|
|
|
|
| ||||||||||||||

 Получите свидетельство
Получите свидетельство Вход
Вход



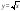 . Графическое решение уравнений и неравенств. Применение при решении задач свойств арифметической и геометрической прогрессии, суммирования бесконечной сходящейся геометрической прогрессии.
. Графическое решение уравнений и неравенств. Применение при решении задач свойств арифметической и геометрической прогрессии, суммирования бесконечной сходящейся геометрической прогрессии.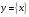 и «целая часть числа»
и «целая часть числа» 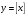 . Метод интервалов для решения неравенств. Преобразования графиков функций: сдвиг, умножение на число, отражение относительно координатных осей. Графические методы решения уравнений и неравенств.
. Метод интервалов для решения неравенств. Преобразования графиков функций: сдвиг, умножение на число, отражение относительно координатных осей. Графические методы решения уравнений и неравенств.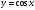 ,
, 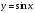 ,
,  ,
,  . Свойства и графики тригонометрических функций.
. Свойства и графики тригонометрических функций.








 Календарно – тематическое планирование по МАТЕМАТИКЕ: АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА, ГЕОМЕТРИЯ 10 класс (углубленный уровень) (56.96 KB)
Календарно – тематическое планирование по МАТЕМАТИКЕ: АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА, ГЕОМЕТРИЯ 10 класс (углубленный уровень) (56.96 KB)
 0
0 569
569 92
92 Нравится
0
Нравится
0


