Получите свидетельство
Вход
a, sinx cos x ≤ a , cos x a , cos x a, cos x tg x ≤ a , tg x a , tg x a, tg x ctg x ≤ a , ctg x a , ctg x a, ctg x түрінде берілген теңсіздіктер тригонометриялық теңсіздіктер деп аталады. Тригонометриялық теңсіздіктерді шешуде қолданылатын алгоритм: тригонометриялық теңсіздікті қарапайым тригонометриялық теңсіздікке келтіру; бір координаталық жазықтыққа теңсіздіктің құрамында берілген тригонометриялық функцияның графигін салу және y = a түзуін жүргізу; функциялар графиктерінің қиылысу нүктелерін табу; берілген теңсіздікті қанағаттандыратын қисықтың бөлігі мен бас аралықты анықтау; сәйкес кері тригонометриялық функцияның мәнін ескеріп, бас аралықтың шеткі нүктелерінің абциссаларының мәнін табу; Тригонометриялық функцияның периодтылық қасиетін пайдаланып, теңсіздіктің жалпы шешімін жазу. " width="640"
Тригонометриялық теңсіздіктер
Анықтама: sin x ≤ a , sin x a , sin x a, sinx
cos x ≤ a , cos x a , cos x a, cos x
tg x ≤ a , tg x a , tg x a, tg x
ctg x ≤ a , ctg x a , ctg x a, ctg x
түрінде берілген теңсіздіктер тригонометриялық теңсіздіктер деп аталады.
Тригонометриялық теңсіздіктерді шешуде қолданылатын алгоритм:
- тригонометриялық теңсіздікті қарапайым тригонометриялық теңсіздікке келтіру;
- бір координаталық жазықтыққа теңсіздіктің құрамында берілген тригонометриялық функцияның графигін салу және y = a түзуін жүргізу;
- функциялар графиктерінің қиылысу нүктелерін табу;
- берілген теңсіздікті қанағаттандыратын қисықтың бөлігі мен бас аралықты анықтау;
- сәйкес кері тригонометриялық функцияның мәнін ескеріп, бас аралықтың шеткі нүктелерінің абциссаларының мәнін табу;
- Тригонометриялық функцияның периодтылық қасиетін пайдаланып, теңсіздіктің жалпы шешімін жазу.
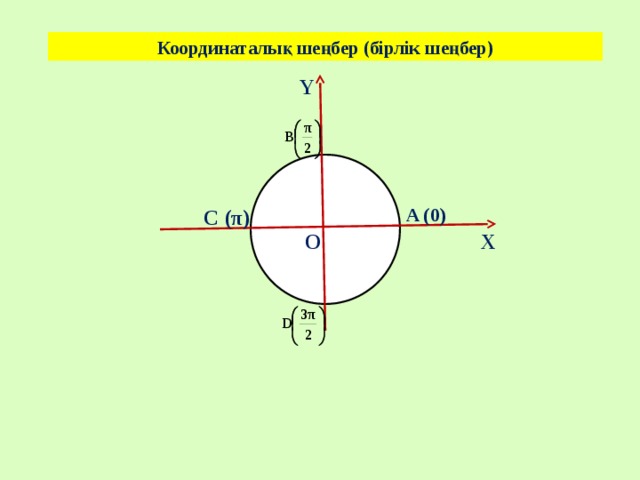
Координаталық шеңбер (бірлік шеңбер)
Y
A (0)
C (π)
X
O
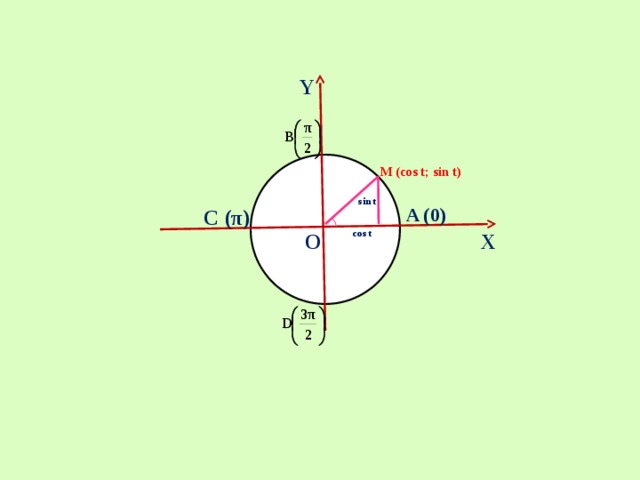
Y
M (cos t; sin t)
sin t
A (0)
C (π)
X
O
cos t
0 Y C (π) A (0) O X 02πn 2πn Z " width="640"
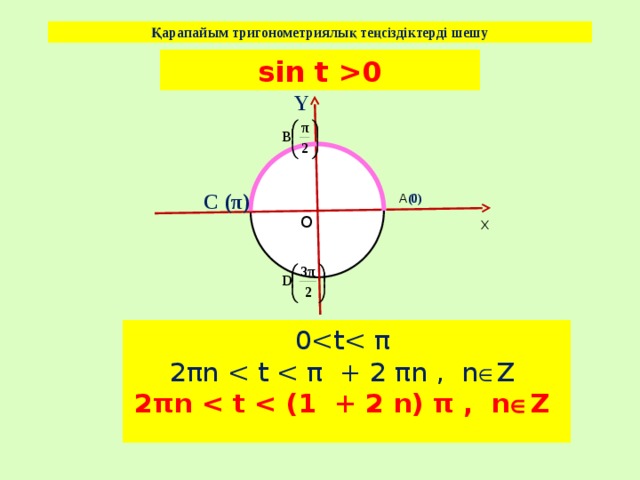
Қарапайым тригонометриялық теңсіздіктерді шешу
sin t 0
Y
C (π)
A (0)
O
X
0
2πn
2πn Z
0 -2π 2π -π O π X 02πk 2πk Z " width="640"
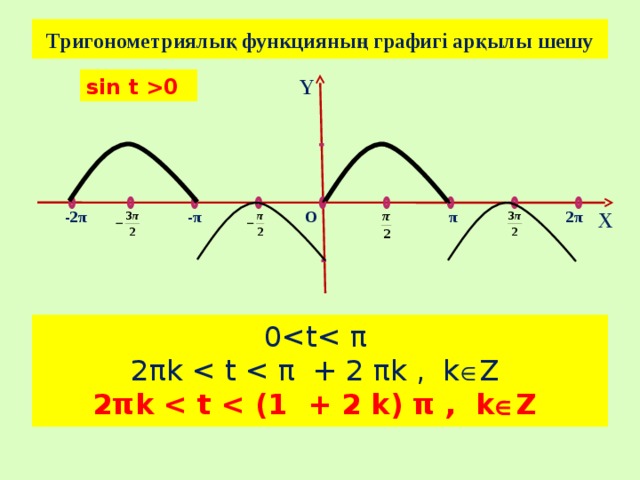
Тригонометриялық функцияның графигі арқылы шешу
Y
sin t 0
-2π
2π
-π
O
π
X
0
2πk
2πk Z
m , -1 Y Y B B N (π-α) M (α) A A C C X O X N M D D α = arcsin m arcsin m arcsin m + 2πn Z " width="640"
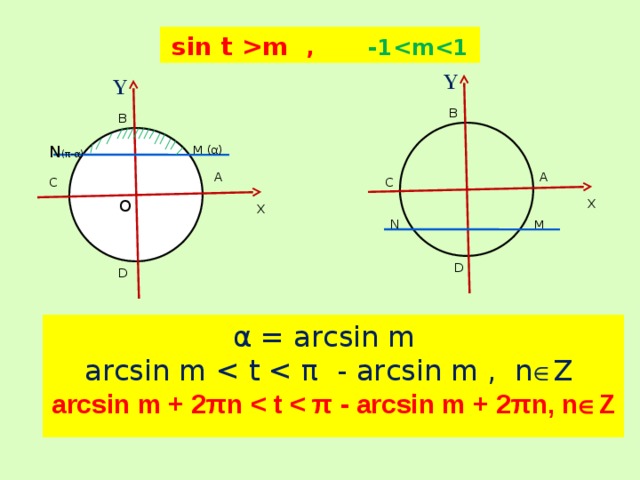
sin t m , -1
Y
Y
B
B
N (π-α)
M (α)
A
A
C
C
X
O
X
N
M
D
D
α = arcsin m
arcsin m
arcsin m + 2πn Z
-m arcsin (-m) + 2πn Z -arcsin m + 2πn Z z = -t -arcsin m + 2πn Z , (-1)-ге көбейтеміз arcsin m + 2πn t - π - arcsin m + 2πn, n Z - π - arcsin m + 2πn Z " width="640"
sin t , -1
t=-z sin(-z) -sin z sin z -m
arcsin (-m) + 2πn Z
-arcsin m + 2πn Z
z = -t
-arcsin m + 2πn Z , (-1)-ге
көбейтеміз
arcsin m + 2πn t - π - arcsin m + 2πn, n Z
- π - arcsin m + 2πn Z
m , -1 Y arccos m A (0) C (π) X O -arccos m -arccos m + 2πn Z " width="640"
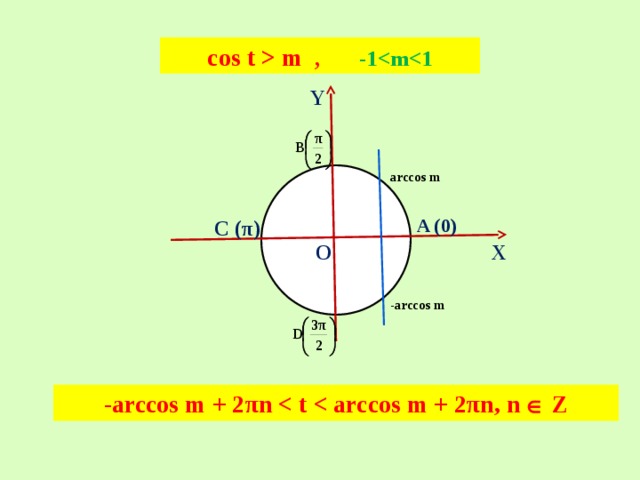
cos t m , -1
Y
arccos m
A (0)
C (π)
X
O
-arccos m
-arccos m + 2πn Z
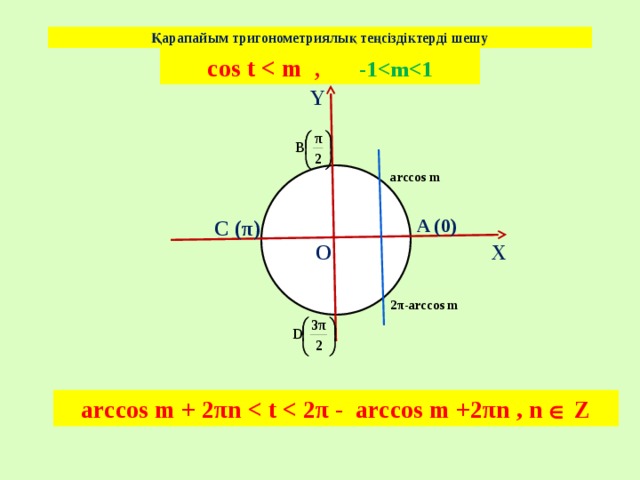
Қарапайым тригонометриялық теңсіздіктерді шешу
cos t , -1
Y
arccos m
A (0)
C (π)
X
O
2π-arccos m
arccos m + 2πn Z
m Y M (arctg m) A (0) C (π) X O arctg m + πn Z " width="640"
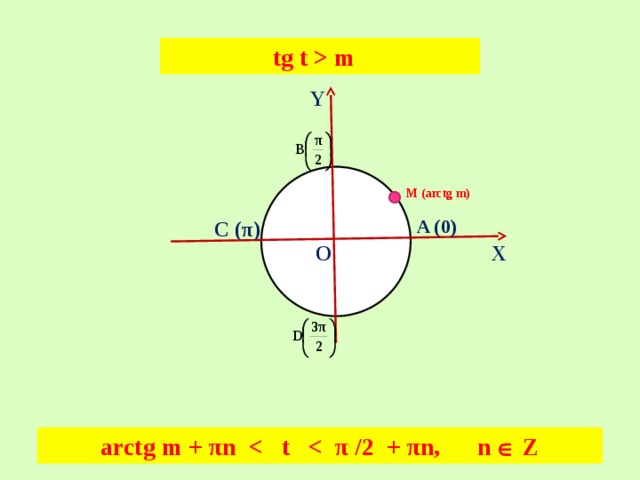
tg t m
Y
M (arctg m)
A (0)
C (π)
X
O
arctg m + πn Z
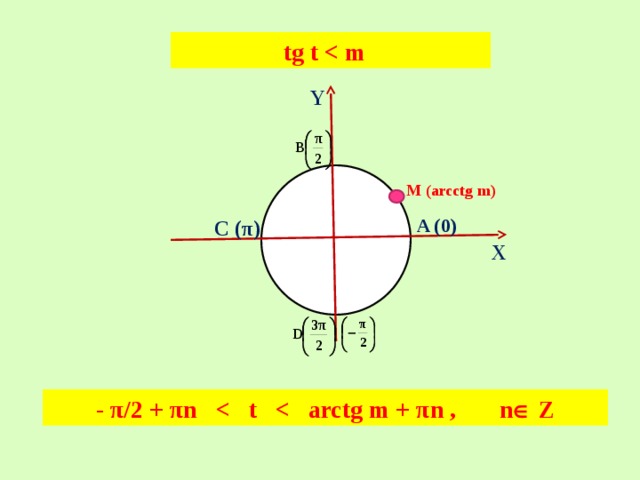
tg t
Y
M (arcctg m)
A (0)
C (π)
O
X
- π/2 + πn Z
m Y M (arcctg m) A (0) C (π) X πn Z " width="640"
ctg t m
Y
M (arcctg m)
A (0)
C (π)
X
πn Z
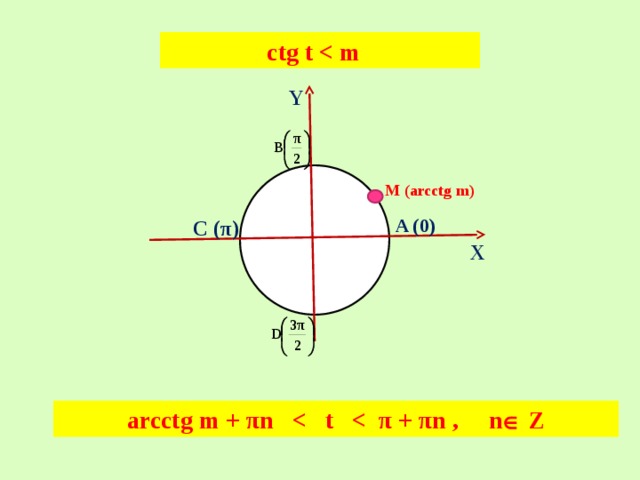
ctg t
Y
M (arcctg m)
A (0)
C (π)
X
arcctg m + πn Z
Қарапайым тригонометриялық теңсіздіктерді шешу. (155.57 KB)
1
15044
344
спасибо, классно