Излучение абсолютно черного тела

В физике часто рассматривается модель, в которой тело находится в термодинамическом равновесии с собственным излучением. В этом случае принято говорить о «чёрном теле» и о «чернотельном излучении». Поле излучения внутри чёрного тела однозначно определяется его температурой. Исследование спектра чёрного тела явилось началом теории атома. Хотя излучение чёрного тела в области малых частот может быть объяснено в рамках классической физики, его полный анализ можно провести только в рамках квантовой теории. Это следует хотя бы из того, что в аналитические формулы, описывающие спектр чёрного тела, входит введённая Планком постоянная ħ. Строго говоря, в природе абсолютно чёрное тело в чистом виде не существует, но его моделью может служить замкнутая полость с малым отверстием (рис.2.1).

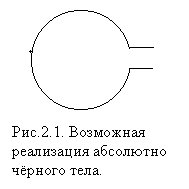
Спектральную плотность излучения чёрного тела будем обозначать U_ω. Её размерность — эрг/(см³·рад/с). Из соотношения

(1) ω = 2π 

между круговой ω и линейной  частотой следует, что U_ω в 2π раз меньше плотности энергии U_, рассчитанной на один герц:

U_ = 2π U_ω.

В теоретических построениях часто пользуются величиной U_ω, а в практических расчётах предпочитают U_. Важную роль в приложениях играет интенсивность излучения, которую для случая чёрного тела принято обозначать B_ω и B_.

Результаты наблюдений часто рассчитываются на единицу длины волны , а не частоты. Соответствующая интенсивность обозначается B_, а плотность энергии — U_. Количество энергии в определённом спектральном интервале, конечно, не зависит от выбора шкалы, поэтому U_ω, U_ и U_ связаны друг с другом соотношением

.

Диапазоны длин волн  и частот ω и  определяются функциональной зависимостью

(3)  = с/ ,  = 2π ω,

из которой следует

.

Следует обратить внимание на то, что спектральные интервалы равны модулям дифференциалов соответствующих переменных. Например, из (2.3) следует отрицательное значение производной d/d, в то время как  и ω существенно положительные величины.

Поле излучения внутри чёрного тела изотропно, поэтому его поток равен нулю. Тем не менее, существует специальная модель, в которой рассматривается не внутренняя область, а граница изотропного источника. Излучение границы анизотропно и, следовательно, поток от неё отличен от нуля. В рамках такой модели справедлив известный закон Стефана–Больцмана для полного, проинтегрированного по всему спектру потока излучения от чёрного тела: поток пропорционален четвёртой степени температуры.

В этом разделе мы изложим основные результаты экспериментов, на которых основана теория излучения чёрного тела.

В диапазоне предельно малых частот,

,

именуемом областью Рэлея–Джинса, плотность энергии пропорциональна температуре T и квадрату частоты ω:

На рис.2.1.1 эта область помечена РД. Формула Рэлея-Джинса может быть выведена чисто

классическим путём, без привлечения квантовых представлений. Чем выше температура чёрного тела, тем шире диапазон частот, в котором справедлива эта формула. Она объясняется в классической теории, но её нельзя распространять на высокие частоты (пунктирная линия на рис.2.1.1), так как просуммированная по спектру плотность энергии в этом случае бесконечно велика:

Эту особенность закона Рэлея-Джинса называют «ультрафиолетовой катастрофой».

В диапазоне больших частот (область В на рис.2.1.1) справедлива формула Вина:

Хорошо видно, что правая часть меняется немонотонно. Если частота не слишком велика, то преобладает множитель ω³ и функция U_ω возрастает. По мере увеличения частоты рост U_ω замедляется, она проходит через максимум, а затем убывает за счёт экспоненциального множителя. Наличие максимума в спектре излучения отличает виновский диапазон от области Рэлея-Джинса.

Чем больше температура тела, тем выше граничная частота, начиная с которой выполняется формула Вина. Величина параметра a в экспоненте правой части зависит от выбора единиц, в которых измеряются температура и частота. Вывод формулы Вина требует привлечения квантовых представлений о природе света.

Закон смещения Вина

Обозначим ω_max частоту максимума функции Планка. Закон смещения Вина гласит, что она пропорциональна температуре, следовательно:

Константа в правой части зависит от выбора единиц частоты и температуры. Кроме того, она различна для функций B_ и B_.

Закон Стефана-Больцмана заключается в том, что плотность энергии чёрнотельного излучения, проинтегрированная по всем частотам, пропорциональна четвёртой степени температуры:

Он часто используется в астрономии при определении светимости звезды по её температуре. Для этого необходимо перейти от плотности излучения к наблюдаемой величине — потоку. Формула для интегрального по спектру потока излучения будет выведена в третьей главе.