Тест №1 по алгебре 10 класса для подготовки к мониторингу
А1. Упростите выражение (sin2x – tg2x)/(cos2x – ctg2x)
1) cos2x; 2) tg6x; 3) ctg4x; 4) -2sin2x
А2.Найдите область определения функции у = 1/(х2 +1)
1) (-1;1); 2) (-∞; -1)U(-1; 1)U(1; +∞); 3) (-1; 1)U(1; +∞); 4) R
А3. Составьте уравнение касательной к графику функции f(x) = (3x2 +2)/(x -1) в точке его пересечения с осью ординат.
1) у = -2х – 2; 2) у = х + 3; 3)у = 2х – 2; 4) у = 7х + 4.
А4. Тело движется прямолинейно по закону х(t) = 3t4 – 2t3 + 1 (х в метрах, t в секундах). Найдите его скорость в момент времени t = 2с.
1) 24; 2) 12; 3) 72; 4) 4.
А5. Решите уравнение cos4x – sin4x = √3/2
1) π/6 + 2 πn, n € Z; 2)+ - π/6 + 2 πn, n € Z; 3) )+ - π/12 + πn, n € Z; 4) иное
А6. Найдите промежутки возрастания функции у = х3 – 
1) (-1/3;1/3); 2) (-∞; -1/3)U(1/3; +∞); 3) (-∞; -1/3); 4) (1/3; +∞)
А7. Найдите ctg(3π/2 + x), если tg x = -2,7
1)-2,7; 2)7,2; 3)-7,2 ; 4) 2,7
А8. Известно, что sin x =  , х – угол 2 четверти. Найдите соs 2x
, х – угол 2 четверти. Найдите соs 2x
1) – 12/13; 2) 119/169; 3) – 119/169; 4) – 10/13
А9. Известно, что g(x) = x  . Найдите gꞌ(3)
. Найдите gꞌ(3)
1) 2,5; 2) 1,7; 3) 2,75; 4) - 4.
А10. sin 3x cos x – cos 3x sin x = √3/2
1)(-1)n π/6 + 1/2 πn, n € Z; 2) )+ - π/12 + πn, n € Z; 3) π/6 + 2 πn, n € Z; 4) иное
В1. Найдите производную функции у = (3х – х2) 
В2. Найдите максимумы и минимумы функции у =  - х
- х
В3. Решите уравнение 3cos2x – sin2x + 4sinx = 0
Тест № 2 для подготовки к мониторингу в 10 классе
А1. Упростите выражение 2 – cos2 x – sin2 x
1) -1; 2) 1; 3) 3; 4) 0.
А2. Какая из перечисленных функций является четной?
1) у = х2 cos x; 2) у = х3 sin x2; 3) у = sin x cos x; 4) у = x2 sin x7
А3. Найдите производную функции у = 2х – 5х6
1) у, = 2х – 30х5 ; 2) у, = 2х - 5 х5; 3) у, = 2 – 30х5; 4) у, = 2 – 5х5
А4. Материальная точка движется по прямой по закону s(t) = 16t – 2t3. Найдите ее скорость в момент времени t = 2.
1) 4; 2) -8; 3) 16; 4) -4.
А5. Решите уравнение sin x =  .
.
1) (-1)n+1 • π/3 + πn, n € Z
2) (-1)n • π/3 + πn, n € Z
3) π/6 + πn, n € Z
4) π/6 + 2πn, n € Z
А6. Функция задана графиком . На каком из указанных промежутков она убывает?

1) [-1;4]
2) [-4;-1]
3) [-3;0]
4) [-4;-3].
А7. Вычислите: 2 sin75 cos75
1) 1/2; 2) -1/2 ; 3) V3/2; 4) -V3/2.
A8. Известно, что sin x = - 3/5 и π
1) – 4/5; 2) 1; 3) 3/4; 4) 4/3
А9. Найдите производную функции у = (4 – 3х)100:
1) 100(4 -3х)99; 2) 300(4 – 3х)99; 3) -300(4 – 3х)99; 4) -3(4х – 3)100.
А10. Решите уравнение cos x + 2cos 2x = 1
1) π + 2 πn, n € Z и (-1)n π/3 + πn, n € Z
2) π + 2 πn, n € Z и arcsin 3/4 + πn, n € Z
3) π + 2 πn, n € Z и arccos 3/4 + 2πn, n € Z
4) π/2 + πn, n € Z и arccos 3/4 + πn, n € Z
В1. Найдите производную функции у = sin 2x – cos 3x:
Проверочная работа по математике для 10 класса
Вариант №1
| № | Задание | |
| 1 |
| |
| 2 |
| |
| 3 |
| |
| 4 |
| |
| 5 |
| |
| 6 |
| |
| 7 |
| |
| 8 |
| |
| 9 | | |
| 10 | | |
Проверочная работа по математике для 10 класса
Вариант № 2
| № | Задание | |
| 1 | ||
| 2 | ||
| 3 | | |
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | | |
| 8 |
| |
| 9 | | |
| 10 | | |

 Получите свидетельство
Получите свидетельство Вход
Вход



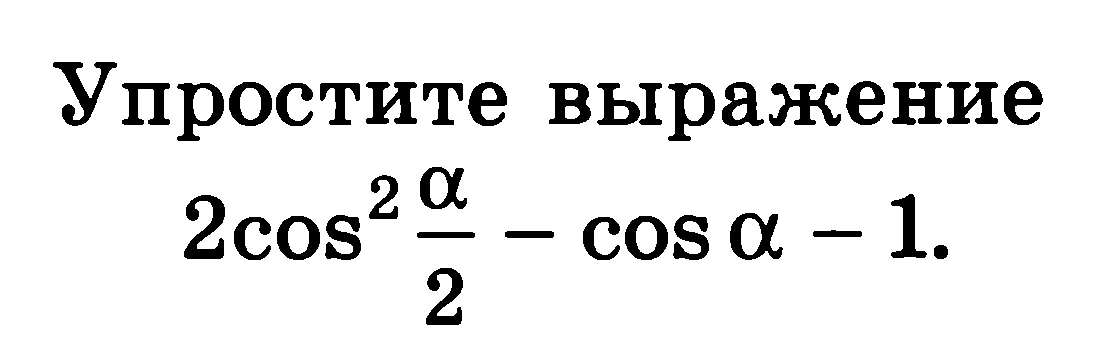

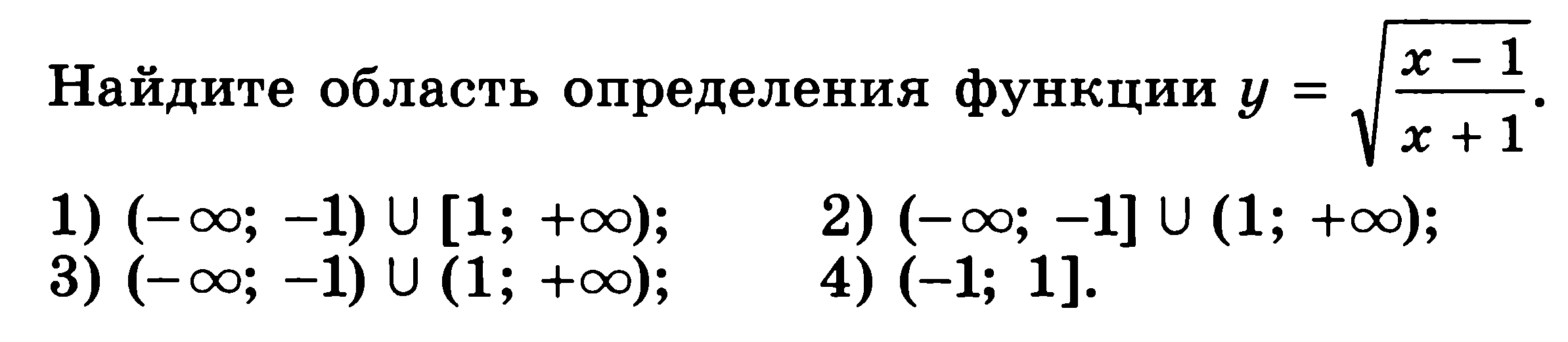









 Итоговые тесты по математике для учащихся 10 класса. (243.37 KB)
Итоговые тесты по математике для учащихся 10 класса. (243.37 KB)
 0
0 1023
1023 35
35 Нравится
0
Нравится
0


